2023年
4月
30日
日
「分からない」を考えよう! #22
生徒たちの「分からない」を取り上げて考えていきます。
解き方が分からない前提で「どんな風に考えて解いていくか」という過程を書いていくので、ぜひご自身でも解き方を考えながら読み進めてみてください。
今回は、中学3年の数学「因数分解」からの出題。塾の教材にあった問題2問、ネットで見つけた問題1問です。新年度最初の中間テストの範囲になるのでしっかり理解して自由自在に扱えるよう勉強しておきましょう!
問題
(1)
x+y=5 , xy=-6 であるとき、( x - y )² の値を求めよ。
(2)
x+y=-4 , xy=3 であるとき、x² + 3xy + y² の値を求めよ。
(3)
a-b=3 , ab=3 であるとき、2a² + 2b² の値を求めよ。
平方完成という考え方を利用して解く問題ですね。
まずは、問題(1) を見ていきましょう。
問題を解くための考え方は、
「( x - y )² の値を求めよ」とあるけど、提示されている値は「x+y=5」となっている。ということは問題の「( x - y )²」が「( x + y )²」だったら値を代入して解けるよね。
となります。
そして、「( x - y )²」を「( x + y )²」に変形させるために平方完成の考え方を使います。
-----
ということで平方完成について説明します。
例えば、「x² + y²」という式があり、これを平方の形、つまり因数分解して「( x + y )²」に変形を完成させるための考え方が平方完成です。
x² + y²
↓
( x + y )²
このように因数分解できるようにしたい。それを考えるために、まずは下の式を展開してみましょう。
x² + y²
↓
x² + 2xy + y²
こうしてみると、和の平方で因数分解するためには「+2xy」が足りないことが分かりますね。ここで必要な考え方はふたつ。
①足りなければ足してあげれば良い
②元の式とイコールの関係を維持するため、勝手に足した式と同じものを引けば良い
つまり①の操作は、
x² + y² ≠ x² + y² + 2xy
右の式になるが、これでは元の式とイコールではなくなってしまうので、
②の操作をして、
x² + y² = x² + y² + 2xy - 2xy
このようにしてあげる。これで「+ 2xy - 2xy」の部分を計算したら元の式「x² + y²」とイコールですよね。この状態で、
x² + y² = ( x² + y² + 2xy ) - 2xy
この部分を因数分解してあげると、
x² + y² = ( x² + 2xy + y² ) - 2xy
x² + y² = ( x + y )² - 2xy
このように、平方プラスα という形に変形させるのが平方完成の考え方です。
では、問題の解説↓
問題(1)
x+y=5 , xy=-6 であるとき、( x - y )² の値を求めよ。

「( x - y )²」の値を求めたい。けど、与えられた値は「x+y=5」となっている。
もし「( x - y )²」が「( x + y )²」だったら「x+y=5」を代入できるのに。
じゃあ「( x - y )²」を「( x + y )²」に変えちゃおう!
ということで、この考え方を実現させるのに使うのが平方完成ですね。具体的な解き方は上記の通りです!
ここまで、なんとなくでも理解できたかな。
しっかり考えて理解できたと思ったら問題(2)(3)は自力で解いてみてください。
解説は↓
問題(2)
x+y=-4 , xy=3 であるとき、x² + 3xy + y² の値を求めよ。

問題(3)
a-b=3 , ab=3 であるとき、2a² + 2b² の値を求めよ。

平方完成についてしっかりと理解し扱えるように勉強してみてください。
ところで、この 問題(1) ですが、生徒が「平方完成を使って解く」ことが出来なかったので取り上げたのですが、この生徒は全く別のアプローチで問題自体は解いています。
私はその考え方をしなかったので凄いなと感心しました。ということで別解。
-----
問題(1)
x+y=5 , xy=-6 であるとき、( x - y )² の値を求めよ。
-----
生徒が目を付けたのは「x+y=5 , xy=-6」このふたつの式。
足して「5」、掛けて「-6」になる x , y の値を考え、
x=(-1) , y=6
を導き出し、( x - y )² に代入して解く。
問題の解き方はひとつじゃないです。ひとつの解き方だけに捉われない柔軟な思考を大切に育てていきたいと思わされました。
ちなみに、この別解のアプローチ。
問題(2) も同様に解くことができますが、問題(3) は厳しいかもしれないですね。少なくとも x, y の値をパッと割り出すことはできそうにないです。
学校の勉強において、基本的に問題の答えは「ひとつ」として用意されているものですが、その答えにたどり着く方法はひとつとは限らないので、自由な発想で解にたどり着くその過程を楽しんでみてくださいね!
以上です。お疲れさまでした!
(*ᴗˬᴗ)⁾⁾
2023年
4月
22日
土
「分からない」を考えよう! #21
生徒たちの「分からない」を取り上げて考えていきます。
解き方が分からない前提で「どんな風に考えて解いていくか」という過程を書いていくので、ぜひご自身でも解き方を考えながら読み進めてみてください。
今回は、中学3年の数学「因数分解」からの出題。高校入試の過去問からですが、少し数字はいじっています。新年度最初の中間テストのテスト範囲になるのでしっかり理解して自由自在に扱えるよう勉強しておきましょう!
問題
次の計算をしなさい。
2023³ - 2023² × 2022 - 2022²
この問題を解こうと思ったら、やり方はふたつあって、
1.力づくで全部計算して解く
2.楽に解ける工夫を考えて解く
なんだけど、こういう問題って基本的には考えて工夫することで楽に解けるように作られています。なので色々工夫して解く努力をしてみましょう。
がんばって考えても「全然分からない」ってなったら解答/解説を見てみましょう。もちろん、それを写して終わりにしちゃだめですよ。それを見たうえで、そこからヒントをつかんで問題を解く糸口にしましょう。
ということで、この問題の解説を見てみます。
-----
与式 = 2023²×(2023-2022)-2022²
-----
はじめの一行だけ見てみると、このように書いてある。私であれば見るのはここだけ。何をどうして、どういう考え方で、式を変形しているのか、「何でこうなるんだろう?」をまずは理解できるように考えます。
たとえば、
①数字の値を「文字」に置き換える。
2023=A , 2022=B とする。
2023³-2023²×2022-2022²
=A³-A²B-B²
このように文字式にすると、式の前半「A³-A²B」を共通因数「A²」で括るのか、っていうことに、気付きやすいのではないかと思います。
ほかにも、
②累乗の表記を全て掛け算に直す。
2023³-2023²×2022-2022²
=(2023×2023×2023)-(2023×2023×2022)-(2022×2022)
このように書いてみても、前半ふたつの式の中に共通因数「2023×2023」があることに気付きやすくなるかもしれないですね。あまりスマートではないですけどね。
問題を解くうえで大切なことは、その過程にある考え方をきちんと理解すること。理解するため、であれば解答/解説を見ながら考えることは全然アリですよ!
それでは私の解答を。↓

なかなか解きごたえのある面白い問題でしたね。
何のために問題を解くのか。宿題や課題が何のために出されるのか。
終わらせることが目的になってしまうと、その努力はただの作業です。
理解することが目的となった努力が「勉強する」ということです。
問題を解く過程の、いろいろな考え方を理解していくことは、その問題だけでなく様々な問題を解くための武器となるので、「分かろう!」っていう勉強を、がんばってくださいね!
以上です。お疲れさまでした!
(*ᴗˬᴗ)⁾⁾
2023年
4月
15日
土
「分からない」を考えよう! #20
生徒たちの「分からない」を取り上げて考えていきます。
解き方が分からない前提で「どんな風に考えて解いていくか」という過程を書いていくので、ぜひご自身でも解き方を考えながら読み進めてみてください。
今回は、中学3年の数学「式の展開」からの出題。いくつかの教材から問題をピックアップしてきました。新年度最初の中間テストのテスト範囲になるのでしっかり理解して自由自在に扱えるよう勉強しておきましょう!
問題
次の式を展開せよ。
(1)
( x + y - 6 ) ( x + y - 8 )
(2)
( x - y + 5 ) ( x - y - 5 )
(3)
( x + 3y - 2 ) ( x + y - 2 )
(4)
( a + b - 3 ) ( a - b - 3 )
(5)
( a + b - 2 ) ( a - b + 2 )
ここで学んでおきたい考え方は、文字の置き換え、です。
もちろん、そんなことをせずに一つひとつ丁寧に計算して解いてもいいんだけど、もっと複雑な問題だとその計算も大変になるかもしれません。
問題を解くうえで色々な考え方を知っていれば、計算がとても楽になるケースもたくさんあるので、ぜひ身に付けておきましょう。
(1) と (2) は基本的な置き換えのパターン。
(3) と (4) は置き換える式がまとまっていないのでちょっとだけ分かりにくいパターン。特に (4) の方は置き換える部分を間違いやすいです。
(5) はそのままでは置き換えができないので符号の操作が必要なパターン。この中では一番難易度が高い問題ですね。
中学3年生は、解説を見る前に自分で解けるかチャレンジしてみてください!
では解説。
↓
問題(1)

置き換えの基本問題その1。x+y=M と置き換えることで、
乗法公式 (x+a)(x+b)=x²+(a+b)x+ab
が利用できる形にりますね。公式の x , a , b の値はそれぞれ M , -6 , -8 となるので、この値で展開。置き換えた M を元に戻します。最後に、
乗法公式・和の平方 (x+a)²=x²+2ax+a²
分配法則 a(b+c)=ab+ac
といった復習も踏まえつつ展開すれば解となります。
問題(2)

置き換えの基本問題その2。x-y=M と置き換えることで、
乗法公式・和と差の積 (x+a)(x-a)=x²-a²
が利用できる形にりますね。公式の x , a の値はそれぞれ M , 5 となるので、この値で展開。置き換えた M を元に戻します。最後に、
乗法公式・差の平方 (x-a)²=x²-2ax+a²
の復習も踏まえつつ展開すれば解となります。
ちょうど (1) (2) を解く過程で乗法公式4つ全部登場するので良い復習になりますね。これらの公式をきちんと扱えないのであればここで勉強しなおしておきましょう。
問題(3)

置き換えに使う共通の値 x , -2 が並びで置いてない、っていうだけ。頭の中できちんと処理できるならそのまま置き換えればいいけれど、自信がないなら一旦並べ替えてから置き換えるのが良いかもしれないですね。
あとは、置き換えて展開、戻して展開、するだけです。
最後に出来上がった多項式の式の並びを整理していますが、これはしてもしなくても大丈夫だと思います。この問題の解答では並べ直していたので、それに倣っています。
並べ方の作法は大まかに、
①次数の大きなものから
②アルファベット順
だけ押さえておけばいいと思います。この問題であれば、
x²=xx , 4xy , 3y²=3yy → 文字2つなので次数は2
-4x , -8y → 文字1つなので次数は1
4 → 文字無しなので次数は0
ということで上のような順に並べています。
個人的にはキレイに並んでいる方が気持ちいいですし、例えば「先生が採点しやすくなれば良いな!」なんて考える優しさがあると素敵だな、って思います。
問題(4)

この問題の間違いやすいポイントは、パッと見て b-3 を置き換えてしまう点。確かにどちらの式にも b-3 が含まれていますが、これは誤り。結構ここ分かっていない子は多いです。
よく見誤るポイントなので気を付けましょう。
この式の値を整理すると、
左側:( a+b-3 ) → a , b , -3
右側:( a-b-3 ) → a , -b , -3
となります。なので b-3 を同じものとしては扱えないということ。共通部分は a-3 となります。あとはこれを別の文字に置き換えて展開、文字を戻して展開すれば解となります。
ちなみのこの問題の解答は展開後の式のままで、特に並べ直しはされていませんでした。そんな感じで「キレイに並べないとダメ」と言ったルールはなく結構アバウトです。並べ直すなら、
a²-b²-6a+9
でしょうか。なのでこの辺りは気楽に考えましょう。
問題(5)

この問題はこのままでは置き換えが使えません。式の値を整理すると、
左側:( a+b-2 ) → a , b , -2
右側:( a-b+2 ) → a , -b , 2
ここで注目する点は b , 2 の符号があべこべになっていること。つまり左側の b , -2 の符号をひっくり返せば -b , 2 となり右側の式と揃えられます。その逆もまた然り。
そこでそのためのテクニックが符号の操作。-1 で括る、という考え方が分かりやすいかな。そうすることで置き換えが使える形に整えることが可能です。
例1: -a+b = -(a-b)
例2: -a-b = -(a+b)
ここさえわかれば、あとは置き換えて展開、戻して展開のいつも通りの処理で解を出せます。
最後に気を付けるポイントは、(b-2)² を展開したときの式を括弧の中に入れておくこと。
-(b-2)² は (-1)×(b-2)² っていう掛け算だから
っていう説明でなんとなく理解できるだろうか。ミスしやすいポイントなので気をつけましょうね。
さて、この問題、ちゃんと理解できたでしょうか?今回の解説では右側の式の -b+2 を括って符号操作したけれど、当然左側の式をいじって解くことも可能です。
ということで、ここまでちゃんと理解できた!と思えたなら、ぜひ左側の式の b-2 の方を符号操作して解くことにチャレンジしてみてください!こんな感じで自分の中の理解を確認することは大切ですよ!
解説は↓
問題(5) 別解

文字に置き換えるときに分かりやすいよう右側の式も整理しています。文字式の計算、符号の扱い、その辺りきちんと理解していれば大丈夫なはず。
よく分からないことが、きちんと分かるようになると楽しいですよね。
勉強がんばって!そして楽しんでください!
最後に。式の置き換えに使用した文字、今回は「M」でしたが、これじゃなきゃダメってことではなくどんな文字を使っても ok です!
問題を見てると「A」や「X」なんかも使ったりしていますが、大文字を使う理由は、式にあるもともとの文字と区別しやすいように、ということだと思います。
小文字の「x」がある問題で置き換えに大文字の「X」を使うと紛らわしいから避けた方がいいかも、とか、いろいろ考えて好きな文字を使って解いてください。
ちなみに、こういった置き換えで「M」をよく使う理由は、
modify 修正する/変更する
の頭文字をとって「M」をよく使う、そういう慣習がある、という感じのようです。
式の展開を置き換えを活用して解く、という本題からはズレた事柄ですが、勉強ってこういう寄り道の方が楽しかったりしますよね。
以上です。お疲れさまでした!
(*ᴗˬᴗ)⁾⁾
2022年
7月
13日
水
「分からない」を考えよう! #19
生徒たちの「分からない」を取り上げて考えていきます。
解き方が分からない前提で「どんな風に考えて解いていくか」という過程を書いていくので、ぜひご自身でも解き方を考えながら読み進めてみてください。
今回は、とある中学の「2年 1学期 期末テスト」で出題された、数学 (連立方程式) の問題です。
問題

この学校の期末テスト (2年 数学) の問題の中では、これが一番難しかったんじゃないかな、と思います。式を立てて連立方程式で解いて x , y を求める、といったシンプルな構成の問題ではないですね。
けど、やってみると意外と簡単に解けてしまいます。
-----
まずは情報の整理から。
①「n」は 3ケタの自然数、一の位は 8 である。
②「n」は "百の位の数" と "十の位の数" と "一の位の数" の和の 28倍と等しい。
この条件を満たす「n」を求めればいいわけですね。また、わざわざ問題文に「すべて」と記載し下線で強調していることから「n」は複数ある可能性が高いです。
ということで、上記 2点から数式を書いていきます。
自然数「n」の 3ケタの数字のうち "百の位の数" と "十の位の数"が分からないので、
百の位の数 → x とする
十の位の数 → y とする
①「n」は 3ケタの自然数、一の位は 8 である。
n = 100x + 10y + 8 ・・・ ①
②「n」は "百の位の数" と "十の位の数" と "一の位の数" の和の 28倍と等しい。
n = (x + y + 8) × 28 ・・・ ②
このように、問題文の記述から 2つの方程式を書くことができる。この時点でそれぞれの方程式に含まれる文字は 3つずつあるので、このままでは解くことはできません。けれど、どちらも「n」を表した式なので①の右辺を②の左辺に代入し一つにまとめることにします。
100x + 10y + 8 = (x + y + 8) × 28 ・・・ ③
これで式に含まれる文字を一つ減らすことができました。それでもこの式を解いて x , y を求めることはできません。
けれどもし x , y のうちどちらかの値が決まってしまえば、残りの文字の値も求めることができますね。だったら決めてしまえばいい、というのがこの問題を解くカギになります。
x と y に当てはまる可能性のある数字について考えます。
それぞれ 3ケタの整数の "百の位の数" と "十の位の数"を表している、ということは当てはまる可能性があるのはどちらも「ひとケタの整数」ということになります。
また、"百の位の数"の方には「0」は当てはまらない (たとえば「018」だと 2ケタの自然数になってしまうから) ということも分かります。
つまり、
x = 1,2,3,4,5,6,7,8,9
y = 0,1,2,3,4,5,6,7,8,9
それぞれの解はこれらの数字だけに絞ることができる、ということ。
あとは式③に順に代入し条件に当てはまる組み合わせを探れば解くことができそうです。たとえば、x=1 のときの y の値を求める、x=2 のときの y の値を求める、といった感じです。
そこでまずは式③を整理します。
100x + 10y + 8 = (x + y + 8) × 28
100x + 10y + 8 = 28x + 28y + 224
50x + 5y + 4 = 14x + 14y + 112
50x - 14x + 4 -112 = 14y - 5y
36x - 108 = 9y
4x - 12 = y
y = 4 ( x - 3 ) ・・・ ③´
この式に x の値を代入し、条件に合う組み合わせを考えます。
まず ( x - 3 ) ですが、この計算がマイナスになる x の値は NG になります。理由は y の値がマイナスになるから。
ということで x = 1,2 は除外。考えるのは x = 3 からで良さそうです。ということで計算していくと、
x = 3 のとき y = 0
x = 4 のとき y = 4
x = 5 のとき y = 8
これ以降は y の値が 2ケタとなり条件に合わなくなるため、文字の値として適当なのはこの 3通りだけということになります。
よって求める解、3ケタの自然数 n は、
A. n = 308, 448, 588
いかがでしたでしょうか。一見、解き方も分からない難しそうな問題かもしれませんが、一つひとつ順に考えていけば意外と簡単に解くことができます。
問題を見て「難しい」「分からない」と思ったとしても、とりあえず分かるところからやってみる、とりあえず問題文から式を考え立ててみる。頭の中で考えるだけではなく、まずはできることから、とりあえずペンを持ちノートを広げて手を動かす!
こういう問題を自分で考えて解くことができるようになってくると、きっと数学が面白く感じるようになるんじゃないかな。ぜひ、チャレンジしてみれください!
-----
問題を解けば終わり、答えが分かれば終わり、ではなく、問題を解く過程でたくさんの「なんだろう?」っていう疑問を見つけて、それを理解していく努力が勉強です。
そしてその「なんだろう?」を解き明かしたときの達成感を味わうのが勉強の醍醐味です!
ぜひたくさんの「分からない」を見つけて、それを「分かった!」に変えていく努力をしていってくださいね!
以上です。お疲れさまでした!
(*ᴗˬᴗ)⁾⁾
2022年
7月
12日
火
「分からない」を考えよう! #18
生徒たちの「分からない」を取り上げて考えていきます。
解き方が分からない前提で「どんな風に考えて解いていくか」という過程を書いていくので、ぜひご自身でも解き方を考えながら読み進めてみてください。
今回は、とある中学の「2年 1学期 期末テスト」で出題された、数学 (連立方程式) の問題です。
問題

これもそんなに難しい問題ではないですね。それでも、数学を「解き方」でしか考えられない場合、当然「解き方」を知らなければ解けない、どうすればいいか分からない、となってしまいます。
数学の文章問題は「解き方」なんて知らなくても「文章を読んで、情報を整理し、考える」ことさえできれば解くことができるので、仮にこの問題の「解き方」を知っていたとしても、それは一旦横に置いておいて、自分で考えて解いてみてくださいね。
-----
ではまず、問題文で提示されている情報を整理してみましょう。
・100円玉が何枚かある。枚数は不明。金額は 枚数×100 で表すことができる。
・500円玉も何枚かある。枚数は不明。金額は 枚数×500 で表すことができる。
・これら全部合わせると 4800円になる。
そのお金を両替した。
・100円 1枚 → 50円 2枚に、つまり枚数は 2倍になる。
・500円 1枚 → 100円 5枚に、つまり枚数は 5倍になる。
・両替後の 100円玉の枚数は、両替後の 50円玉の枚数より、9枚多い。
言い換えると「100円玉の枚数」引く「50円玉の枚数」が「9枚」ということ。
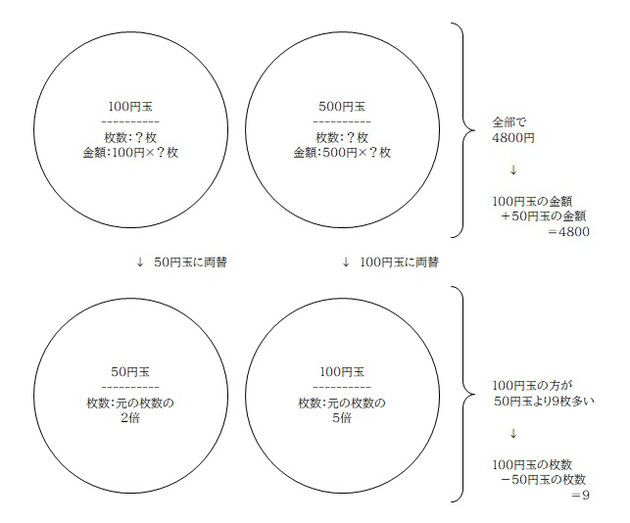
こんな感じでしょうか。これを数式にするために分からない値を記号に置いて考えます。問題の (1) で「x枚の 100円玉」と記述があるので、
元の 100円玉の枚数:x枚
元の 500円玉の枚数:y枚
とし、整理します。
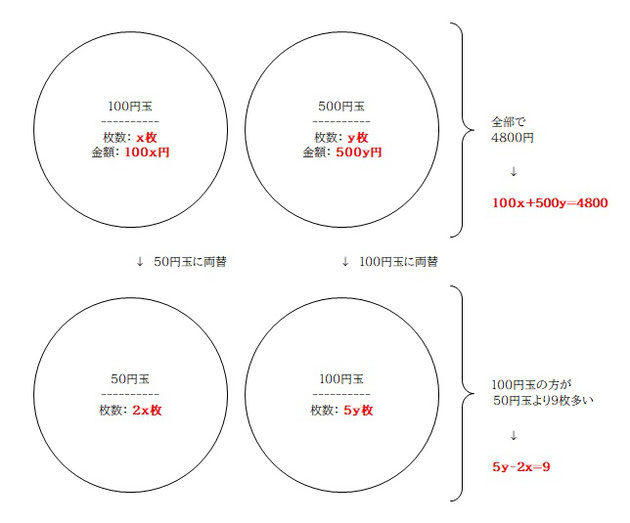
ここまで整理すればあとはただの計算問題ですね。
-----
(1)
この問題の肝は両替後の枚数をきちんと数式で表すことができるかどうか。わざわざ小問でそこの確認をさせてくれています。
問題文を読んで情報の整理をしっかりとしていればすでに答えは出ていますね。
A. (1) 2x
-----
(2)
この問題も、すでに方程式ふたつ完成しているのであとは解くだけ。
元の 100円玉の枚数:x枚
元の 500円玉の枚数:y枚
としているので x , y の値を求めればそれがそのまま答えですね。
100x+500y=4800 ・・・ ①
5y-2x=9 ・・・ ②
解き方は色々、どう解くのも自由ですが、なるべく大きい数字は扱わないほうが楽なので、まずは①の式を 100 で割って、
x+5y=48
これを 2倍します。
2x+10y=96 ・・・ ①´
②の式は x と y の項の並びが逆なので、これも整理して、
-2x+5y=9 ・・・ ②´
x の項がプラスとマイナスなので①´と②´を足して連立方程式を解きます。
2x+10y=96
-2x+5y=9
15y=105
y=7
これを①´に代入。
2x+70=96
2x=26
x=13
A. (2) 100円玉:13枚、500円玉:7枚
そういえば文章問題って答えが正しいかどうか、確認することもできます。求めた答えで問題文の通りになるかを確認するだけ。
100円玉 13枚 → 1300円、500円玉 7枚 → 3500円
金額を合計すると 4800円
100円玉 13枚を 50円玉に両替 → 26枚、500円玉 7枚を 100円玉に両替 → 35枚、
35-29=9 で、両替後の 100円玉の方が 9枚多い
すべて問題文の条件を満たしていますね。
求めた解に自信がなければ、こうやって確認するといいですよ!
-----
問題を解けば終わり、答えが分かれば終わり、ではなく、問題を解く過程でたくさんの「なんだろう?」っていう疑問を見つけて、それを理解していく努力が勉強です。
そしてその「なんだろう?」を解き明かしたときの達成感を味わうのが勉強の醍醐味です!
ぜひたくさんの「分からない」を見つけて、それを「分かった!」に変えていく努力をしていってくださいね!
以上です。お疲れさまでした!
(*ᴗˬᴗ)⁾⁾
2022年
7月
11日
月
「分からない」を考えよう! #17
生徒たちの「分からない」を取り上げて考えていきます。
解き方が分からない前提で「どんな風に考えて解いていくか」という過程を書いていくので、ぜひご自身でも解き方を考えながら読み進めてみてください。
今回は、とある中学の「2年 1学期 期末テスト」で出題された、数学 (連立方程式) の問題です。
問題

この問題は、「2つの連立方程式の解は同じ」、これの意味をきちんと理解できるかどうか、がポイントかな。そこさえ分かれば、あとは、
1. 連立方程式を解き x , y を求める。
2. x , y を代入、方程式を解き a を求める。
3. x , y を代入、方程式を解き b を求める。
これだけなので簡単ですね。では解いていきます。
まずは「2つの連立方程式の解は同じ」ということについて。解が同じになるということは、4つの方程式のうち、連立方程式をどの組み合わせで解いても x , y の値が同じになるということ。
連立方程式の勉強をしている時点では、次の単元である一次関数は当然習っていないのだけれど、「2つの連立方程式の解は同じ」ということがどういうことかを簡単に理解するために一次関数のグラフで考えてみます。
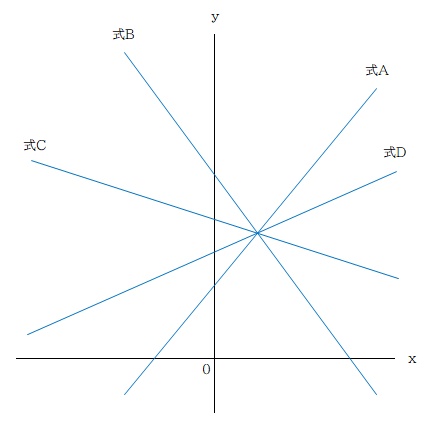
グラフにするとこんなイメージかな。
すべての解は同じ → x , y が同じ → すべての式 (直線) の交点が同じ
っていう感じ。どの式の組み合わせで連立方程式を解いても良いということになります。
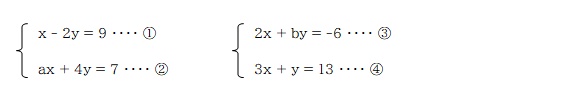
ひとつの方程式のなかに文字 (分からない値) が3つ含まれている式②③は使えないので、式①④を連立方程式で解けば良い、ということですね。
ここさえ理解できればあとはただの計算問題です。
x - 2y = 9 ・・・ ①
3x + y = 13 ・・・ ④
①を 3倍して、
3x - 6y = 27 ・・・ ①´
①´から④を引く
3x - 6y = 27
3x + y = 13
-7y = 14
y = -2
y の値を①に代入
x - 2y = 9
x + 4 = 9
x = 5
x=5 , y=-2 を式②③に代入し a , b を求める
ax + 4y = 7
5a - 8 = 7
5a = 15
a = 3
2x + by = -6
10 - 2b = -6
-2b = -16
b = 8
A. a=3 , b=8
この問題は、最初に式①②と式③④がセットで提示されているので、「解が同じ」の意味をちゃんと考えられないと、「式②③で連立方程式で解けばいいんだ!」という発想に至らないのかもしれないですね。
一次方程式も連立方程式も、他のどんな単元の文章問題もすべて同じですが、問題を解くために必要な情報は全て問題文の中に用意されています。
大切なのは与えられた情報をちゃんと読み解くこと。
ちなみに勉強ができない子は「問題文を読んで考える」のではなく「問題文を見て解き方を知ってる問題かどうかを判断している」だけのことが多い。
なので、そういう子の「先生、この問題分かりません」という質問は「先生、この問題の解き方を知りません」ということが大半です。
文章問題を解けるようになりたいなら、まずは問題文をちゃんと読んで考えること!
勉強頑張ってくださいね!
----
問題を解けば終わり、答えが分かれば終わり、ではなく、問題を解く過程でたくさんの「なんだろう?」っていう疑問を見つけて、それを理解していく努力が勉強です。
そしてその「なんだろう?」を解き明かしたときの達成感を味わうのが勉強の醍醐味です!
ぜひたくさんの「分からない」を見つけて、それを「分かった!」に変えていく努力をしていってください。
以上です。お疲れさまでした!
(*ᴗˬᴗ)⁾⁾
2022年
7月
08日
金
「分からない」を考えよう! #16
生徒たちの「分からない」を取り上げて考えていきます。
解き方が分からない前提で「どんな風に考えて解いていくか」という過程を書いていくので、ぜひご自身でも解き方を考えながら読み進めてみてください。
今回は、とある中学の「2年 1学期 期末テスト」で出題された、数学 (式の計算) の問題です。
問題

文章から式を立てて解くのではなく、式を立てて等式変形する問題。解き方を覚える勉強をしている子は、こういう変化球に弱いです。
早速解いていきましょう。まずは情報の整理。
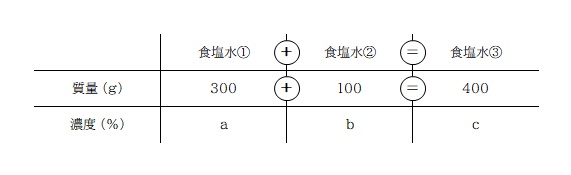
食塩水の質量は足して式にすることができるけど、濃度の方はそのまま足せるものではないですね。なので、食塩水の質量と濃度から、食塩水に含まれる食塩の質量を文字式で表しましょう。それであれば足して方程式にすることが可能です。
濃度の計算は、例えば食塩水① の場合、300g を 100個 とした時の a個分が食塩の量になります。なので、300g の a/100 で表すことができますね。
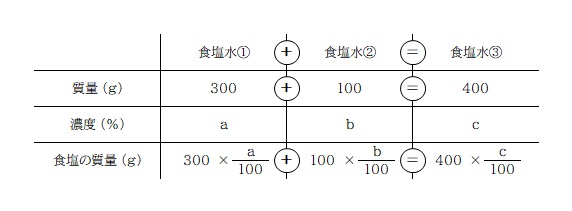
あとは、食塩の質量で作った方程式を整理し c= の形にするだけ。
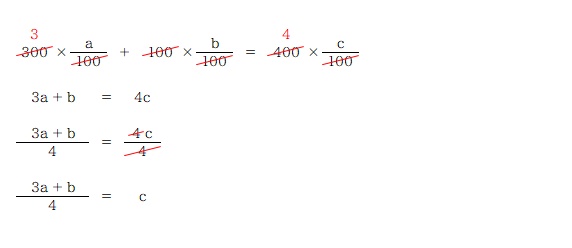

特に難しい問題というわけではないですが、普通に式を解いて質量やら濃度を求める問題の解き方を覚える勉強をしていると、こういう風に少し捻った出題をするだけで「分からない!」ってなって思考停止してしまいます。
文章問題は「覚えた解き方通りに解く」のではなく、「問題文を読んで考えて解く」よう意識して勉強してください。
-----
問題を解けば終わり、答えが分かれば終わり、ではなく、問題を解く過程でたくさんの「なんだろう?」っていう疑問を見つけて、それを理解していく努力が勉強です。
そしてその「なんだろう?」を解き明かしたときの達成感を味わうのが勉強の醍醐味です!
ぜひたくさんの「分からない」を見つけて、それを「分かった!」に変えていく努力をしていってくださいね!
以上です。お疲れさまでした!
(*ᴗˬᴗ)⁾⁾
2022年
7月
07日
木
「分からない」を考えよう! #15
生徒たちの「分からない」を取り上げて考えていきます。
解き方が分からない前提で「どんな風に考えて解いていくか」という過程を書いていくので、ぜひご自身でも解き方を考えながら読み進めてみてください。
今回は、とある中学の「2年 1学期 期末テスト」で出題された、数学 (連立方程式) の問題です。
問題

「速さ」の計算は苦手な子が多いイメージですが、いろんな単元の文章問題に登場してくるので、分からなかったり不正解になったときにきっちり見直しをして理解しておくようにしましょう。
数学だけでなく理科でも速さの計算はたびたび登場するので、きちんと理解しておくと様々な場面で勉強が楽になると思いますよ。
-----
ということで、まずは問題を解く前に速さの計算について。
中学生なら「みはじ」などで公式を覚えるのではなく、それぞれの計算の意味を理解しておきましょう。
「速さ」は、単位時間あたりに進む距離を表しています。
つまり、1分あたり何メートル進む、だとか、1時間あたり何キロメートル進む、といった感じですね。
例えば、350m 進むのに 7分かかった場合、350 を 7 で割れば 1分あたり何メートル進むのかを求めることができます。

「距離」は、速さと時間が分かっていれば求めることができます。
例えば、分速50m の速さで 7分歩いたとする。1分で 50m 進む速さで 7分歩く、つまり 1分の 7倍の時間歩くのだから、1分で進む距離の 7倍の距離を進めるということ。
なので、1分で進む距離 50m × 7 で進んだ距離を求めることができますね。

「時間」を求める計算、距離÷速さ、は一番分かりにくいかもしれないですね。
これは「速さ」を、「1分あたり 50m 進む」ではなく「50m 進むのに 1分かかる」と考えると分かりやすいのかもしれません。
350m の距離を分速50m で進む場合、350m の中に 50m がいくつあるかを考える。それが「距離÷速さ」350÷50 で、50m が 7つあるから 350m 進むのに 7分かかるということ。

速さ、距離、時間、に関係とそれぞれの計算の意味もきちんと理解して、公式を覚えてないと計算できない、なんていうことの無いようにしておきましょう。
では、問題を解いていきましょう。まずは情報の整理から。
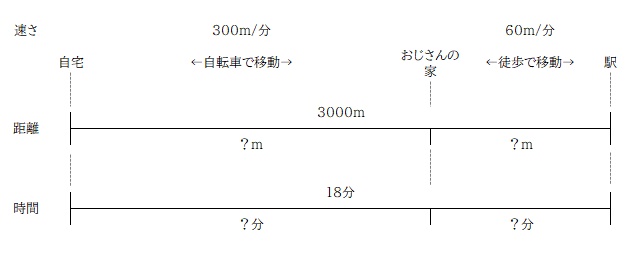
問題で問われているのは「自転車で走った道のり」なので、距離をそれぞれ x , y とおいて式を立てるのが良さそうですね。
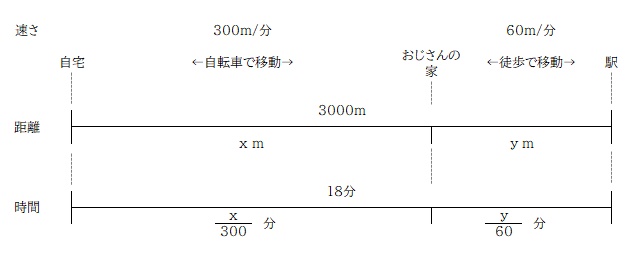
自転車で走った距離を x とすると、自転車で走った時間を 距離÷速さ で表すことができます。歩いた距離を y とし、こちらも同様に時間を y を使って表します。
距離の合計が 3000m、時間の合計が 18分なので、方程式をふたつ立てることができるので、あとは連立方程式で解くだけ。
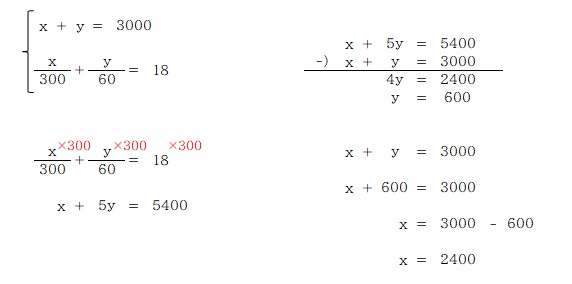
A. 2400m
先の解き方では、距離を x , y とおいて式を立てましたが、時間の方を x , y としても当然解くことができます。
問題の解き方を覚えただけ、ではあまり意味がないので文章問題の指導をするときは子どもたちに大抵の場合こう言います。
「じゃあ次は時間の方を x , y とおいて解いてみて!」と。
ということで別解。
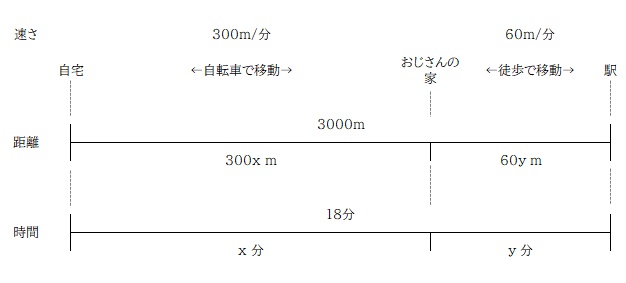
自転車で走った時間を x とすると、自転車で走った距離を 速さ×時間 で表すことができます。歩いた時間を y とし、こちらも同様に距離を y を使って表します。
時間の合計が 18分、距離の合計が 3000m なので、方程式をふたつ立てることができるので、あとは連立方程式で解くだけ。
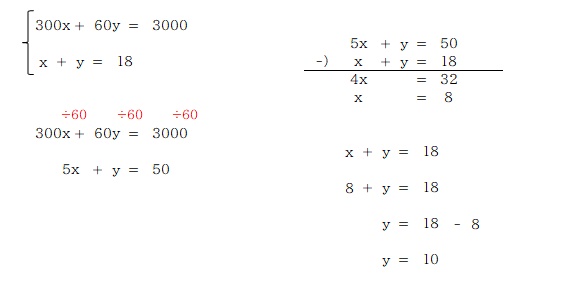
ということで x と y を求めることができましたが、もちろんこれは答えではありません。問われているのは「走った道のり」で、計算で求めた x , y の値は「走った時間」と「歩いた時間」です。
数学の文章問題を「解き方」でしか覚えない子はこういうところで躓きます。式の意味、計算の意味、何を文字において、計算の結果何を求めたのか、をきちんと考えながら問題を解く癖をつけましょう!
計算の結果、「x」、つまり走った時間が 8分だと分かりました。分速 300m で 8分間走ったのだから、走った距離は 300×8 で 2400m が解となります。
また、走った時間を x とした時、走った距離は 300x と表しているのだから、そこに x=8 を代入して、300×8 で 2400m と考えても良いですね。
A. 2400m
問題の解き方を覚える。そういう勉強をしている子は応用が利きません。問題で問う内容を一部だけ、ほんの少し変えるだけで正解できなくなったりします。
例えば、この問題だとちょっと意地悪して「走った道のりは何km ですか?」と少しだけ求める答えの単位を変えるだけで正解できなくなったりします。
理由は「覚えた解き方」のなかに「求めた解の単位を変える」という工程が含まれていないから。
逆に「覚えた解き方」のなかに「求めた解の単位を変える」という工程が含まれていた場合、類題を解くときに、する必要のない「単位を変える計算」をして不正解になるパターンもあったりします。
問題を解く過程、その計算の意味を理解しようとしないと、このように全く応用が利かなくなるということが多々あります。
問題を解くための計算の仕方を覚える勉強ではなく、問題を解くための計算の意味を一つひとつきちんと理解しようとする、そういう勉強をしていって欲しいものですね。
-----
問題を解けば終わり、答えが分かれば終わり、ではなく、問題を解く過程でたくさんの「なんだろう?」っていう疑問を見つけて、それを理解していく努力が勉強です。
そしてその「なんだろう?」を解き明かしたときの達成感を味わうのが勉強の醍醐味です!
ぜひたくさんの「分からない」を見つけて、それを「分かった!」に変えていく努力をしていってくださいね!
以上です。お疲れさまでした!
(*ᴗˬᴗ)⁾⁾
2022年
7月
06日
水
「分からない」を考えよう! #14
生徒たちの「分からない」を取り上げて考えていきます。
解き方が分からない前提で「どんな風に考えて解いていくか」という過程を書いていくので、ぜひご自身でも解き方を考えながら読み進めてみてください。
今回は、とある中学の「2年 1学期 期末テスト」で出題された、数学(式の計算) の問題です。
問題
次の計算をしなさい。

これだけ?そうです。たったこれだけの基本的な計算問題です。
けれど、子どもたちがよく間違えるポイントがふたつもあるので、その点も踏まえてみていきたいと思います。
-----
◆間違いやすいポイント、その1:方程式の計算と混同している。

このように、12 をかけて分数の分母を処理しようとして間違うパターン。これは方程式の勉強をしてきた中学2年生の子がよくやる間違い。
方程式の場合は「両辺に同じ数をかける」から左辺と右辺のイコールの関係が崩れず成り立つのであって、文字式の場合はこのまま計算しただけでは正解することはできないです。

式に 12 をかける、ということは、イコールの向こう側にある「この計算の解」も 12倍されることになるからですね。そのことをきちんと理解していればこの方法で解くことも可能です。それは後ほど。
-----
◆間違いやすいポイント、その2:符号ミス。

マイナスの分数で分子が多項式になっているとき、その多項式中の + や - の符号ミスが多いです。これは文字式でも方程式でも同じ。
計算の仕方をきちんと理解していないと本当によく間違うポイントのひとつですね。
では、解いていきます。
この計算式は方程式ではないので、基本の解き方としては通分して分母を揃え計算を進めていきます。
通分した後、x の項と y の項をそれぞれ計算するため、
「12 分の 2x-8y」を
「12 分の 2x」と「12 分の 8y」に分けるときの符号に注意です。
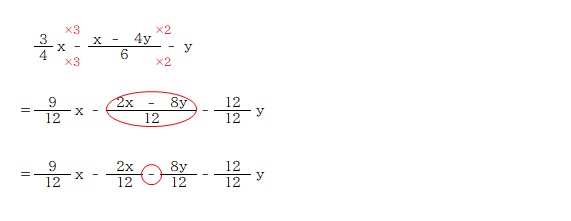
このように「マイナス」にしてしまうのは不正解です。
この計算は「2x から 8y を引いたものを前の数から引いている」のであって、「2x と 8y 両方を前の数から引いている」のではないからですね。
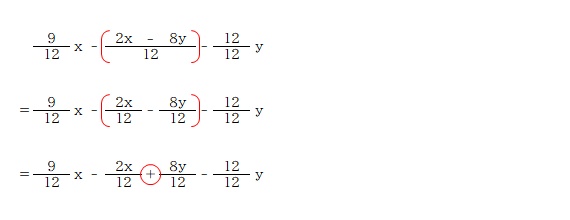
このように括弧を書いて計算すると間違いにくくなると思います。
あとは普通に計算するだけ。

次は、方程式のように分母を処理する方法での計算について。

この計算方法でも同じようにこの部分で符号ミスが多いです。なので先ほどの通武運の計算のとき同様、括弧を付けて考えると間違いにくくなります。
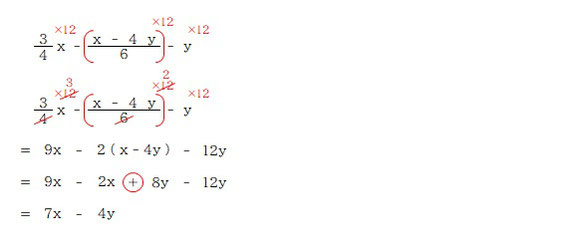
このように符号は + が正解。間違えないように気を付けましょう。
そして最後に、この計算方法は式を 12倍しています。ということは、そこから求められた答えも 12倍されているということ。
つまりここでの解「7x-4y」は本来の答えを 12倍したもの、ということになります。
言い換えると「7x-4y」を 12分の 1 にすれば本来の解になるということ。

一つひとつの計算の意味をきちんと理解していれば、どちらの解き方でも問題なく解くことができます。
しっかり理解して自由自在に扱えるように勉強頑張ってください!
問題を解けば終わり、答えが分かれば終わり、ではなく、問題を解く過程でたくさんの「なんだろう?」っていう疑問を見つけて、それを理解していく努力が勉強です。
そしてその「なんだろう?」を解き明かしたときの達成感を味わうのが勉強の醍醐味です!
ぜひたくさんの「分からない」を見つけて、それを「分かった!」に変えていく努力をしていってくださいね!
以上です。お疲れさまでした!
(*ᴗˬᴗ)⁾⁾
2022年
7月
01日
金
「分からない」を考えよう! #13
生徒たちの「分からない」を取り上げて考えていきます。
解き方が分からない前提で「どんな風に考えて解いていくか」という過程を書いていくので、ぜひご自身でも解き方を考えながら読み進めてみてください。
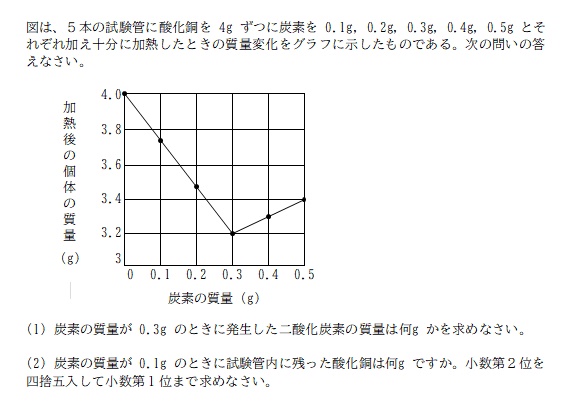
今回は、とある中学の授業で出されたプリントからの出題、理科(2年、化学) の問題です。
(1)
炭素 0.3g の試験管について考える。
酸化銅 4.0g に炭素 0.3g を入れているので、試験管内の物質の質量は 4.3g となる。それを加熱し終えたら 3.2g になっていたので、加熱前→加熱後で消失した 4.3 - 3.2 = 1.1g が二酸化炭素の質量であると考えられる。
A. (1) 1.1g
ちなみに、炭素の質量が 0.1g ~ 0.3g までは右下がり、0.4g ~ 0.5g が右上がりのグラフになっているのは、炭素 0.3g で酸化銅の中の酸素すべてと反応しきってしまい余った炭素が試験管内に残るから。
酸化銅 4.0g の中の銅と酸素の質量は、
銅:酸素:酸化銅 = 4:1:5
= 3.2g:0.8g:4.0g
となるので、炭素 0.3g の試験管の実験では、炭素 0.3g と酸素 0.8g すべてが反応し二酸化炭素 1.1g となって消失、銅 3.2g だけが試験管内に残った、ということになりますね。
なので炭素の量を 0.3g から増やしても、増やした炭素と反応するだけの酸素はもうないので、二酸化炭素となって消失する量も変わらず 1.1g のまま。
炭素 0.4g の試験管
→酸素 0.8g と炭素 0.3g が反応し二酸化炭素 1.1g となって消失、
銅 3.2g と余った炭素 0.1g の計 3.3g が試験管内に残った。
炭素 0.5g の試験管
→酸素 0.8g と炭素 0.3g が反応し二酸化炭素 1.1g となって消失、
銅 3.2g と余った炭素 0.2g の計 3.4g が試験管内に残った。
となるので、炭素 0.3g 以降のグラフは右上がりのグラフになっているということ。
問題を解くだけではなく、こんな感じできちんと理解していれば還元反応の様々なパターンの出題に対応できると思います。
(2)
炭素 0.1g ということは、炭素 0.3g の「3分の1」だということ。
考え方はとてもシンプルです。
つまり、反応した酸化銅の質量も「3分の1」ということになり、反応せずに残った酸化銅の質量は「3分の2」ということになりますね。
4.0 × 2/3 = 2.666・・・ ≒ 2.7
A. (2) 2.7g
ちなみに炭素 0.1g の試験管ですが、「加熱後の個体の質量」をグラフで見ると 3.7g よりちょっと多いくらいのところを通っていますね。
「あれ?試験管内に残った酸化銅の質量って 2.7g なのに何で?」って思った人は勉強のチャンスです!
試験管内に残った「加熱後の個体の質量」が何を指しているか。これは、
「炭素と反応し還元されて残った銅の質量 + 炭素と反応せずに残った酸化銅の質量」
となります。
問題 (2) の解は「炭素と反応せずに残った酸化銅の質量」なので、「炭素と反応し還元されて残った銅の質量」について求める必要がありますね。反応した酸化銅の質量も「3分の1」なので、
4.0 × 1/3 = 1.333・・・
この酸化銅の質量 1.333・・・g に含まれる銅と酸素それぞれの質量を求めます。
銅:酸素:酸化銅 = 4:1:5
= 1.066・・・g:0.266・・・g:1.333・・・g
質量 1.333・・・g の酸化銅に含まれる酸素 0.266・・・g と反応し還元されて銅 1.066・・・g が残った、ということになりますね。
よってグラフの点、炭素 0.1g の試験管の「加熱後の個体の質量」は、
1.066・・・ + 2.666・・・ = 3.733・・・
という値になり、グラフの点の位置とも合致することが分かります。
炭素 0.2g のときの値についても求めて、炭素 0.1g ~ 0.5g それぞれの各種値もすべてまとめて整理してみました。
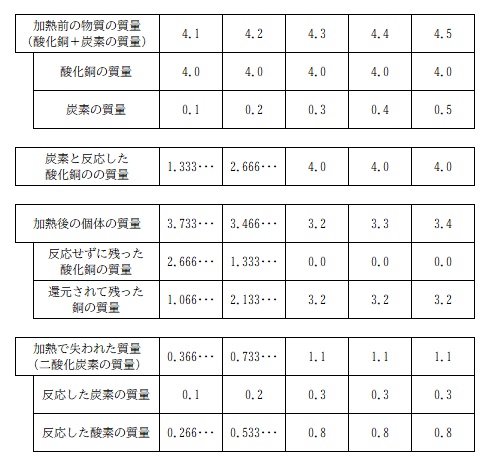
勉強の参考までに。多分あってると思います。解答があるわけではないので確認はできませんが、何回も計算して確認したので。
問題で問われている内容に対してだけ答えを出して、ハイ終わり、ではなく、分からないことがひとつも残ってない!ってくらいまでとことん考えて、完璧に理解しようって努力する。これが勉強だと私は思っています。
(1)(2) のたった2つの問題でもこれだけ色々なことを学ぶことができるんですね。
ここまでやれば、酸化銅の還元、もちろん酸化銅以外であってもですが、どんなパターンの出題があっても解くだけの力が付くのではないかと思います!
-----
問題を解けば終わり、答えが分かれば終わり、ではなく、問題を解く過程でたくさんの「なんだろう?」っていう疑問を見つけて、それを理解していく努力が勉強です。
そしてその「なんだろう?」を解き明かしたときの達成感を味わうのが勉強の醍醐味です!
ぜひたくさんの「分からない」を見つけて、それを「分かった!」に変えていく努力をしていってくださいね!
以上です。お疲れさまでした!
(*ᴗˬᴗ)⁾⁾
2022年
6月
30日
木
「分からない」を考えよう! #11#12 別解
生徒たちの「分からない」を取り上げて考えていきます。
解き方が分からない前提で「どんな風に考えて解いていくか」という過程を書いていくので、ぜひご自身でも解き方を考えながら読み進めてみてください。
今回は、6/28 と 6/29 に投稿した記事の問題の別解についてです。
問題

一昨日の記事に書いた考え方でも良いのだけれど、「鉄粉と銅粉の混合物」「硫化鉄と硫化銅の混合物」の質量がもっと大きな値になった場合はあの解き方だときっと大変なんですよね。
なので、記事を書いた後もずっと他の解き方を考えていたのですが、昨夜寝る前にふと閃いたので解説したいと思います。
(4)
鉄と硫化鉄、銅と硫化銅、それぞれの比率を元に考える。
鉄:硫化鉄 = 7:11
銅:硫化銅 = 2:3
硫黄については「十分な量を混ぜ」と記載があるので、特に考える必要はないです。上記比率をそのまま質量と考え、鉄粉と銅粉の混合物が 20g、硫化鉄と硫化銅の混合物が 31g になるように考える。
ここまでは同じ。
鉄と硫化鉄の比率を変えずに質量を調整したい場合、両方を同じ倍率で増減させればいいが、その「何倍すればいいか」が分からない。なので、その倍率を x として考えれば良い。
銅と硫化銅も同様。こちらの倍率は y として考える。
鉄:硫化鉄 = 7:11 ← x倍する
銅:硫化銅 = 2:3 ← y倍する
鉄:硫化鉄 = 7x:11x
銅:硫化銅 = 2y:3y
それぞれ必要な質量をこのように表すことができる。
鉄粉と銅粉の混合物が 20g なので、
7x + 2y = 20
硫化鉄と硫化銅の混合物が 31g なので、
11x + 3y = 31
あとはこの二つの式を連立方程式で解けば、それぞれの倍率を求めることができる。
計算についてはここでは割愛。
x=2 , y=3
計算結果はこのようになるので、
鉄:硫化鉄 = 7×2:11×2
= 14g:22g
銅:硫化銅 = 2×3:3×3
= 6g:9g
倍率を代入すればそれぞれの質量を求めることができます。この問題は「混合物 20g の中の鉄粉の質量」を求める問題なので、
A. (4) 14.0g
問題

こちらの問題も考え方は全く同じ。前に問題の解説を読んで「分かった!」と思えたのなら、この問題の解説を読む前に、ぜひ自分の力で解いてみてください!
(3)
銅と酸化銅、マグネシウムと酸化マグネシウム、それぞれの比率を元に考える。
銅:酸化銅 = 4:5
マグネシウム:酸化マグネシウム = 3:5
酸素については「十分に酸素と化合させ」と記載があるので、特に考える必要はないです。上記比率をそのまま質量と考え、銅とマグネシウムの混合物が 3.1g、酸化銅と酸化マグネシウムの混合物が 4.5g になるように考える。
銅と酸化銅の比率を変えずに質量を調整したい場合、両方を同じ倍率で増減させればいいが、その「何倍すればいいか」が分からない。なので、その倍率を x として考えれば良い。
マグネシウムと酸化マグネシウムも同様。こちらの倍率は y として考える。
銅:酸化銅 = 4:5 ← x倍する
マグネシウム:酸化マグネシウム = 3:5 ← y倍する
銅:酸化銅 = 4x:5x
マグネシウム:酸化マグネシウム = 3y:5y
それぞれ必要な質量をこのように表すことができる。
銅とマグネシウムの混合物が 3.1g なので、
4x + 3y = 3.1
酸化銅と酸化マグネシウムの混合物が 4.5g なので、
5x + 5y = 4.5
あとはこの二つの式を連立方程式で解けば、それぞれの倍率を求めることができる。
計算についてはここでは割愛。
x=0.4 , y=0.5
計算結果はこのようになるので、
銅:酸化銅 = 4×0.4:5×0.4
= 1.6g:2.0g
マグネシウム:酸化マグネシウム = 3×0.5:5×0.5
= 1.5g:2.5g
倍率を代入すればそれぞれの質量を求めることができます。この問題は「元の混合物 3.1g の中のマグネシウムの質量」を求める問題なので、
A. (3) 1.5g
このように問題の解き方っていうのはひとつではないし、さまざまな考え方で解くことができたりします。
ひとつの解き方が分かったとしても、何か納得できないひっかかりが少しでも残っているなら「何か他にもっといい解き方、考え方はないだろうか」って突き詰めてみるのも楽しいものです!
問題を解けば終わり、答えが分かれば終わり、ではなく、問題を解く過程でたくさんの「なんだろう?」っていう疑問を見つけて、それを理解していく努力が勉強です。
そしてその「なんだろう?」を解き明かしたときの達成感を味わうのが勉強の醍醐味です!
ぜひたくさんの「分からない」を見つけて、それを「分かった!」に変えていく努力をしていってくださいね!
以上です。お疲れさまでした!
(*ᴗˬᴗ)⁾⁾
2022年
6月
29日
水
「分からない」を考えよう! #12
生徒たちの「分からない」を取り上げて考えていきます。
解き方が分からない前提で「どんな風に考えて解いていくか」という過程を書いていくので、ぜひご自身でも解き方を考えながら読み進めてみてください。
今回は、とある中学の授業で出されたプリントからの出題、理科(2年、化学) の問題です。
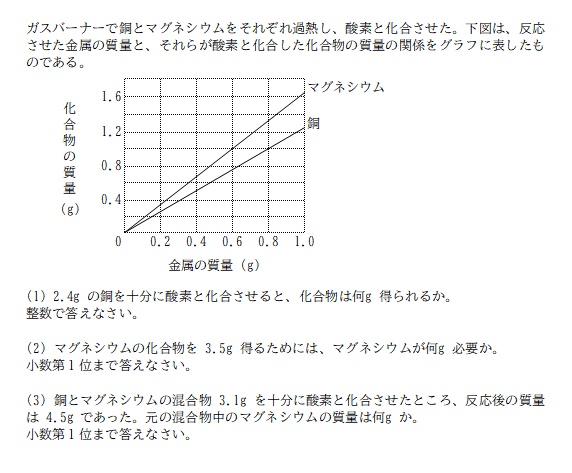
昨日の記事(「分からない」を考えよう! #11)を読んで「分かった!」と思えたなら解ける問題です。
勉強は「分かった!」と思っただけでは終わりではありません。「分かった!」と思ったなら、それが本当なのかどうかを確認し「分かった!、ということを証明する」ところまでやってはじめて勉強したといえます。
本当に「分かった!」のか、「分かった気になった」だけなのか、その確認のためにもぜひチャレンジしてみてください。
(1)
グラフから必要な情報を読み取ります。
縦線と横線の交点を銅のグラフが通る場所を探すと、金属の質量 0.8g / 化合物の質量 1.0g の点を通っていることが分かる。
銅 0.8g が酸化し、酸化銅 1.0g ができているので、この値を整数の比に整理する。酸素の質量については特に考える必要はない。
銅:酸化銅 = 0.8:1.0
= 8:10
= 4:5
この比率を利用して銅 2.4g に対する酸化銅の質量を求めれば良い。
銅:酸化銅
4:5 = 2.4:x
4x = 12
x = 3
A. (1) 3.0g
(2)
これも先の問題同様、グラフから必要な情報を読み取ります。
縦線と横線の交点をマグネシウムのグラフが通る場所を探すと、金属の質量 0.6g / 化合物の質量 1.0g の点を通っていることが分かる。
マグネシウム 0.6g が酸化し、酸化マグネシウム 1.0g ができているので、この値を整数の比に整理する。酸素の質量については特に考える必要はない。
マグネシウム:酸化マグネシウム = 0.6:1.0
= 6:10
= 3:5
この比率を利用して酸化マグネシウム 3.5g の元になったマグネシウムの質量を求めれば良い。
マグネシウム:酸化マグネシウム
3:5 = x:3.5
5x = 10.5
x = 2.1
A. (2) 2.1g
(3)
銅と酸化銅、マグネシウムと酸化マグネシウム、それぞれの比率を元に考える。
銅:酸化銅 = 4:5
マグネシウム:酸化マグネシウム = 3:5
酸素については「十分に酸素と化合させ」と記載があるので、特に考える必要はないです。上記比率をそのまま質量と考え、銅とマグネシウムの混合物が 3.1g、酸化銅と酸化マグネシウムの混合物が 4.5g になるように考える。
ここからは分かりやすいように、
銅とマグネシウムの混合物 3.1g → 31g
酸化銅と酸化マグネシウムの混合物 4.5g → 45g
というように 10倍した値で考ることにします。
銅+マグネシウムが 31g (奇数) ということは、銅 (偶数) + マグネシウム (偶数) という組み合わせにはならないことが分かる。銅「4」は何倍しても偶数なので、マグネシウム「3」の方を奇数にするよう考える。
銅:酸化銅、マグネシウム:酸化マグネシウム、の比率をそのまま質量として、銅とマグネシウムの混合物 31g、酸化銅と酸化マグネシウムの混合物 45g になる組み合わせを探していく。
マグネシウム:酸化マグネシウム = 3g:5g
11倍すると 33g:55g → どちらも問題文にある値を超えるので NG
9倍すると 27g:45g → これだと酸化マグネシウムが問題文にある値を超えるので NG
7倍すると 21g:35g
→ (銅:酸化銅 = 4g:5g) を 2.5倍した (10g:12.5g) を混ぜ合わせると
31g:47.5g となるので NG
5倍すると 15g:25g
→ (銅:酸化銅 = 4g:5g) を 4倍した (16g:20g) を混ぜ合わせると
31g:45g となるのでこの割合で混ぜ合わせるのが正解!
となり問題文と合致する質量を求めることができましたね。31g と 45g は本来の質量を考えやすいように 10倍にした値なので、
銅:酸化銅 = 1.6g:2.0g
マグネシウム:酸化マグネシウム = 1.5g:2.5g
で混ざり合っていると考えることができる。よって元の混合物中のマグネシウムの質量は、
A. (3) 1.5g
いかがでしたか?
前回の記事を読んで、その問題を解く考え方をちゃんと理解できていたなら、今回の問題も解くことができるはずです。
解くことができないということは、残念ながら前回の記事の問題を「ちゃんと理解できていなかった」可能性が高い、ということになります。
最初にも書きましたが、「分かったと思う」ことがひとつの勉強のゴールではないです。「分かったと思ったことを、本当に分かったのか確認し証明する」ことまでやってはじめてひとつの勉強のゴールだと言えるのです。
問題が解けて分かったと思えたなら、必ずその類題を探してチャレンジするようにしてくださいね!
-----
問題を解けば終わり、答えが分かれば終わり、ではなく、問題を解く過程でたくさんの「なんだろう?」っていう疑問を見つけて、それを理解していく努力が勉強です。
そしてその「なんだろう?」を解き明かしたときの達成感を味わうのが勉強の醍醐味です!
ぜひたくさんの「分からない」を見つけて、それを「分かった!」に変えていく努力をしていってくださいね!
以上です。お疲れさまでした!
(*ᴗˬᴗ)⁾⁾
2022年
6月
28日
火
「分からない」を考えよう! #11
生徒たちの「分からない」を取り上げて考えていきます。
解き方が分からない前提で「どんな風に考えて解いていくか」という過程を書いていくので、ぜひご自身でも解き方を考えながら読み進めてみてください。
今回は、とある中学の授業で出されたプリントからの出題、理科(2年、化学) の問題です。
問題
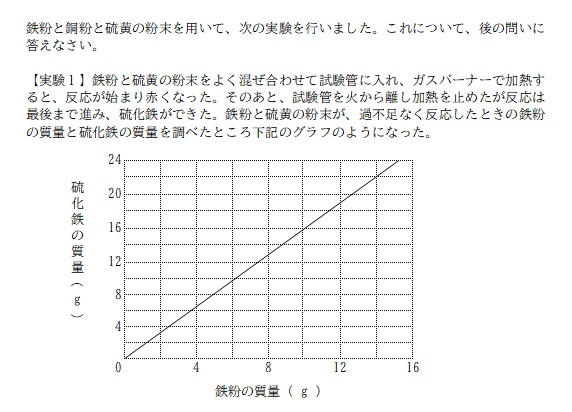

今回から、記事の構成や書き方をこれまでとは変えて、できるだけシンプルに、なるべく短く、を心がけて書いていきます。
(1)
グラフから必要な情報を読み取ります。
縦線と横線の交点をグラフが通る場所を探すと、鉄粉 14g / 硫化鉄 22g であることが分かる。
そこから反応した硫黄の質量を求めると、22-14=8 で、硫黄 8g となる。
これらの情報から3つの物質の質量比を求めると、
鉄:硫黄:硫化鉄 = 14:8:22
= 7:4:11
となる。あとはこの比率を利用して硫化鉄 16.5g に対する硫黄の質量を求めれば良い。
硫黄:硫化鉄
4:11 = x:16.5
11x = 66
x = 6
A. (1) 6.0g
(2)
この問題も (1) で使った「鉄/硫黄/硫化鉄」の比率を使って解くことができる。
気を付けるポイントは、鉄粉 26.8g が全て反応したのか、一部が反応し余りが出たのか、という点。もちろん、硫黄 12.0g について同様に考えても良い。
ここの意味が分かっていないと 26.8+12.0=38.8g の硫化鉄!みたいな間違った回答をすることになる。
ますは、鉄粉 26.8g が完全に反応するのに必要な硫黄の質量を考えてみる。
鉄:硫黄
7:4 = 26.8:x
7x = 107.2
x = 15.3・・・
となるので、鉄粉 26.8g が完全に反応するには硫黄 12.0g だけだと少し足りないことが分かる。言い方を変えると、この硫黄の量では鉄粉は全て反応せず余る、ということ。
つまり、鉄粉 26.8g が全て反応して何g の硫化鉄になるか、ではなく、硫黄 12.0g が全て反応して何g の硫化鉄になるか、を考えれば良い。
硫黄:硫化鉄
4:11 = 12:x
4x = 132
x = 33
A. (2) 33.0g
(3)
実験2の問題文に書いてある、銅と硫化銅の質量から反応した硫黄の質量を求め、それらの情報から3者の質量の比率を求める。
硫化銅 5.1 - 銅 3.4 = 硫黄 1.7
銅:硫黄:硫化銅 = 3.4:1.7:5.1
= 2:1:3
銅の原子と硫黄の原子が1:1で結びつく、と記載があるので上記の質量比率がそのまま原子1個の質量比率となることが分かる。
問題 (1) で求めた鉄/硫黄/硫化鉄の質量比率、
鉄:硫黄:硫化鉄 = 7:4:11
これも上記の質量比率がそのまま原子1個の質量比率となる。問題文を読んでも鉄の原子と硫黄の原子の結びつきが1:1という記述はないが、硫化鉄の化学反応式「Fe+S→FeS」を知っていれば考えることができる。
ここまでで、銅と硫黄、鉄と硫黄、それぞれの原子1個の質量比率が分かったが、銅と鉄の質量比率を求めるには2つの比率の中で共通する硫黄の比率を揃えて比較する必要があるので、
鉄:硫黄 = 7:4
銅:硫黄 = 2:1 ← こっちを 4倍して硫黄の比率を揃える
鉄:硫黄 = 7:4
銅:硫黄 = 8:4
よって、鉄の原子1個と銅の原子1個の質量の比は 7:8 となる。
A. (3) 7:8
(4)
鉄と硫化鉄、銅と硫化銅、それぞれの比率を元に考える。
鉄:硫化鉄 = 7:11
銅:硫化銅 = 2:3
硫黄については「十分な量を混ぜ」と記載があるので、特に考える必要はないです。上記比率をそのまま質量と考え、鉄粉と銅粉の混合物が 20g、硫化鉄と硫化銅の混合物が 31g になるように考える。
鉄+銅が 20g (偶数) ということは、鉄 (奇数) + 銅 (偶数) という組み合わせにはならないことが分かる。銅は何倍しても偶数なので、鉄の方を偶数にするよう考える。
鉄が 7 の 4倍だと 28 となり問題文の 20g を超えてしまうので使えるのは 2倍の 14g しかないと考えることができる。そこに銅を加えて 20g にするには、銅 2 を 3倍して足せば良い。
鉄:硫化鉄 = 7:11 ← 2倍
銅:硫化銅 = 2:3 ← 3倍
鉄:硫化鉄 = 14:22
銅:硫化銅 = 6:9
これで混ぜ合わせると、
鉄+銅:硫化鉄+硫化銅 = 20:31
となり問題文と合致する質量を求めることができましたね。よって鉄と銅の混合物の中の鉄の質量は 14g であると分かります。
A. (4) 14.0g
いかがでしたか?
私だったらこんな風に考えて解くかな、という解説です。他にも解き方、考え方はいろいろあると思います。そういうのを考えたり調べて勉強するのも面白いかもしれません。
特別な化学の知識がないと解けない、というような問題ではなく、問題の中の情報を整理し考えれば解ける問題だと思います。個人的にはこういう「考えれば解ける問題」は好きですね。
-----
問題を解けば終わり、答えが分かれば終わり、ではなく、問題を解く過程でたくさんの「なんだろう?」っていう疑問を見つけて、それを理解していく努力が勉強です。
そしてその「なんだろう?」を解き明かしたときの達成感を味わうのが勉強の醍醐味です!
ぜひたくさんの「分からない」を見つけて、それを「分かった!」に変えていく努力をしていってくださいね!
以上です。お疲れさまでした!
(*ᴗˬᴗ)⁾⁾
2022年
6月
19日
日
「分からない」を考えよう! #10
生徒たちの「分からない」を取り上げて考えていきます。
解き方が分からない前提で「どんな風に考えて解いていくか」という過程を書いていくので、ぜひご自身でも解き方を考えながら読み進めてみてください。
今回は、塾にあるワークからの出題、数学(2年 連立方程式) の問題です。
問題

今回は、昨日の記事(「分からない」を考えよう! #9)で解いた問題と同じ、割合の計算を含む連立方程式の文章問題です。
なので、昨日の記事を読んでしっかりと勉強をした子なら簡単に解ける問題!
そのはず、なんだけど。
解くことはできる、なのに、正解できない。
そんなトラップが仕掛けられた問題です。ホントはトラップなんていう大層なものではないのだけれど、「昨日の問題を解いている」ということで引っかかる子、気づけない子は多いです。
正解を出せるかどうか、ぜひチャレンジしてみてください。
Let's think!
問題文から分かっていること。
・去年の生徒数は、男女合わせて 480人
・今年は、去年と比べて、
- 男子が 10%減った
- 女子が 4%増えた
- 全体で 13人減った
これを昨日と同じように表に書き込みます。

去年の男子と女子の数が分からないので x , y として考えます。

男子は去年 x人いて、今年はそこから 10%減った、
つまり去年を 100%としたとき今年は 90%になった。なので 0.9 を掛ければいい。
女子は去年 y人いて、今年はそこから 4%増えた、
つまり去年を 100%としたとき今年は 106%になった。なので 1.06 を掛ければいい。
合計は去年の人数から減った分を引けばいいですね。

男子と女子の和が合計なので、

これで2つ式ができたので、あとは連立方程式で解けばいいですね。
-----
②の式に 100を掛けて小数をなくす。

①の式に 90を掛けて、x の項を②´の式と揃える。
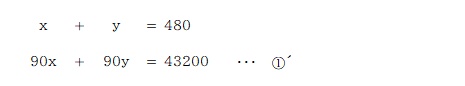
②´の式から①´の式を引いて y を求める。
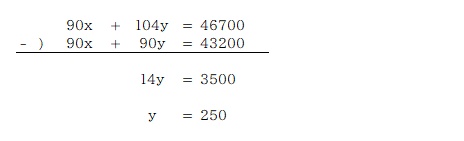
①の式に y の値を代入、x を求める。

ということで、
男子の人数 230人、女子の人数 250人
なのですが!
これが答えだと思った子は残念ながら不正解です。
なぜでしょう。たてた式は正しいです。計算も間違っていません。x と y の値も間違っていません。けど正解ではありません。
なんでなのか?考えてみてください。
Let's think!
なんで正解にならないのか、分かりましたか?
不正解を言い渡し見直しをさせると、生徒は必ずノートを見直します。式が間違っていないか、計算が間違っていないか、けどどちらも間違っていません。
なかなか不正解になった理由に気付けません。
それもそのはず。見直すべきは式や計算といった問題を解く過程ではないからですね。そもそもの前提が間違っています。
なので見直すべきは「問題文」です。
よく読んでみましょう。最後の一文です。
「今年の男子、女子それぞれの生徒数を求めよ。」
求めるのは去年の人数ではなく、今年の人数なんですね。なのでこの解き方で x , y を求めるだけだと不正解になってしまうのです。
とても簡単なことですが、この手の問題を解いたことがあって、表面的な問題の解き方だけを覚える勉強に慣れてしまっている子、なんかはホントによく引っ掛かります。

ということで、この問題の解を求めるには連立方程式で解いた x , y の値を、今年の人数である、男子:0.9x と、女子:1.04y に代入して解としないといけないというわけ。
今年の男子の人数:
0.9x = 0.9×230 = 207人
今年の女子の人数:
1.04y = 1.04×250 = 260人
A. 今年の男子:207人、女子:260人
となります。
-----
ちなみに連立方程式の解がそのまま正解にならないのは、「去年の人数を x , y 」としているからです。
なので「今年の人数を x , y」として解けば、その解がそのままこたえになりますね。
せっかくなので考えてみてください。
難しいポイントは、10%減った/4%増えた、というのが「去年の人数」の対する割合だということ。そこの計算をどうするかですね。
ヒントは税込みの値段を、税込み前の元の値段に戻す計算、を考えればいいですね。
Let's think!
今年の人数を x , y としたとき、去年の人数を x , y を使った数式で表さないといけません。
よくある間違いで、
去年→今年:10%減った、今年→去年:10%増やせばいい
去年→今年:4%増えた、今年→去年:4%減らせばいい
と考えてしまう子もいたりしますが、
10%減った/4%増えた、というのはあくまで「去年の人数」の対する割合なので、これでは不正解。
考え方は、
男子の人数は、去年を 100% としたとき、今年は 90% なのだから、
今年を 90% と考え、それを 100% に戻せば去年の人数になる。
女子の人数は、去年を 100% としたとき、今年は 104% なのだから、
今年を 104% と考え、それを 100% に戻せば去年の人数になる。
という感じ。
もっとシンプルに考えるなら、
たとえば、5倍した数を元の数に戻したいなら?
→5 で割ればいいよね。
というだけの話。
つまり、
男子、去年の人数に 0.9 を掛けたのが今年の人数、ということは
→今年の人数を 0.9 で割れば去年の人数になる。
女子、去年の人数に 1.04 を掛けたのが今年の人数、ということは
→今年の人数を 1.04 で割れば去年の人数になる。

なので、式にするとこんな感じ。割合の考え方、その計算、しっかりと理解して使いこなせるようにしておきましょうね。
あとは、計算していくだけ。
ただ計算は、去年を x , y としたときよりも少しめんどくさくなります。
-----
まずは③の式を連立方程式で解きやすい形に変形していきます。

④の式に 90を掛けて、x の項を③´の式と揃える。
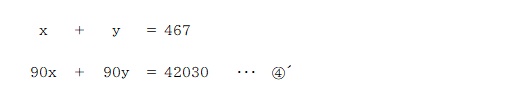
③´の式から④´の式を引いて y を求める。
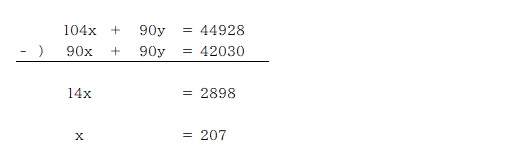
④の式に y の値を代入、x を求める。

先ほどの正解と同じ解を得ることができましたね。
問題の解き方はひとつではありません。
問題を解けば終わり、答えが分かれば終わり、ではなく、問題を解く過程でたくさんの「なんだろう?」っていう疑問を見つけて、それを理解していく努力が勉強です。
そしてその「なんだろう?」を解き明かしたときの達成感を味わうのが勉強の醍醐味です!
ぜひたくさんの「分からない」を見つけて、それを「分かった!」に変えていく努力をしていってくださいね!
以上です。お疲れさまでした!
(*ᴗˬᴗ)⁾⁾
2022年
6月
18日
土
「分からない」を考えよう! #9
生徒たちの「分からない」を取り上げて考えていきます。
解き方が分からない前提で「どんな風に考えて解いていくか」という過程を書いていくので、ぜひご自身でも解き方を考えながら読み進めてみてください。
今回は、とある中学のワークからの出題、数学(2年 連立方程式) の問題です。
問題

連立方程式の文章問題。特別難しいというわけではありませんが、割合の計算、その考え方をきちんと理解していないと解けません。
この記事の投稿時はちょうど1学期の期末テスト前なので、2年生はしっかり勉強してテストに備えておきましょう!
あと、この問題は連立方程式の問題として出題されていますが、一次方程式でも解くことができます。なので1年生もぜひチャレンジしてみてください。
Let's think!
解ける子はすぐ解けたと思います。
分からない!って子は一緒に考えていきましょう。
文章問題を解くコツは、提示された情報をきちんと整理して考えること。
整理すべき情報はまず3つ。
「男子の数」「女子の数」「全体の数」
これら3つの情報をさらに、
「昨年度」「今年度」
の2つの軸でそれぞれ考える必要がありますね。
私が教えるときは次のように書いて考えさせます。

こういう感じの簡単な表に、問題文に書かれている情報、何を x や y といった文字に置き換えるか、を書き込みながら整理していきましょう。
Let's think!
問題文から分かっていること。
・昨年度の生徒数は、男女合わせて 650人
・今年度は、昨年度と比べて、
- 男子が 4%減った
- 女子が 6%増えた
- 全体で 4人増えた
これを表に書き込みます。

このように整理することができます。
なので昨年度の男子と女子の数を文字に置き換えて考えるのが良さそうですね。
昨年度の男子の数を「x」、女子の数を「y」としましょう。

では次に今年度のところを考えていきます。
合計は 650人から 4人増えた、ということなので 654人ですね。
問題は男子の数と女子の数。
ここを文字を使った数式に置き換えましょう。
Let's think!
ここから少し「問題を解く」という本筋から逸れますが、「問題を解く」ために必要な考え方を学ぶために寄り道しましょう。
割合の計算について。
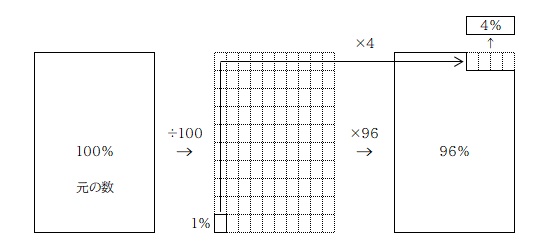
これが問題文にある「4%減った」の考え方。
「4%減る」ということは「96%になった」と言い換えることができるので、「100 を 96 にする」という考え方がひとつ。
計算の仕方は次の通り。

もうひとつは「100 の中の 4 を求めて、元の数から引く」という考え方。
計算の仕方は次の通り。

二通りの考え方、その違いは、
前者は、百分率の状態で 100% から 4% を引いて考えていて、
後者は、元の数の 4% の数を求めて実際の数を引いている、
つまり 4% を減らす計算を「百分率の状態でする」か「実際の数でする」かという違いですね。考え方としては両方理解しつつ、計算については前者の方法を身につけましょう。そのほうが簡単だし扱いやすいです。
ここまでの説明の「元の数」を「1200円」として例を挙げておきます。
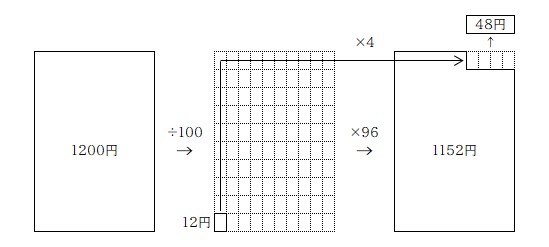
1200円の 4%: 1200×0.04=48円
1200円の 4%減(96%): 1200×0.96=1152円
スーパーでよく見る「20%OFF」とか「4割引き(40%引き)」なんかも同じように計算できますので、いろいろ試してみてください。
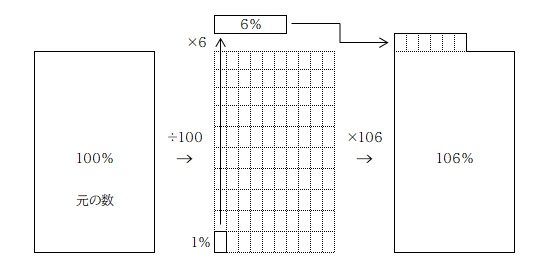
今度は問題文にある「6%増えた」の考え方。
「6%増える」ということは「106%になった」と言い換えることができるので、「100 を 106 にする」という考え方がひとつ。
計算の仕方は次の通り。
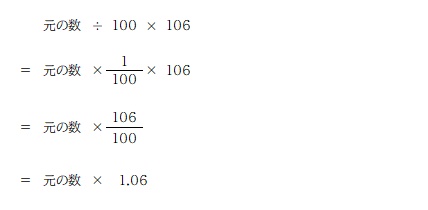
もうひとつは「100 の中の 6 を求めて、元の数に足す」という考え方。
計算の仕方は次の通り。

二通りの考え方、その違いは、
前者は、百分率の状態で 100% に 6% を足して考えていて、
後者は、元の数の 6% の数を求めて実際の数を足している、
つまり 6% を増やす計算を「百分率の状態でする」か「実際の数でする」かという違いですね。考え方としては両方理解しつつ、計算については前者の方法を身につけましょう。そのほうが簡単だし扱いやすいです。
ここまでの説明の「元の数」を「1200円」として例を挙げておきます。
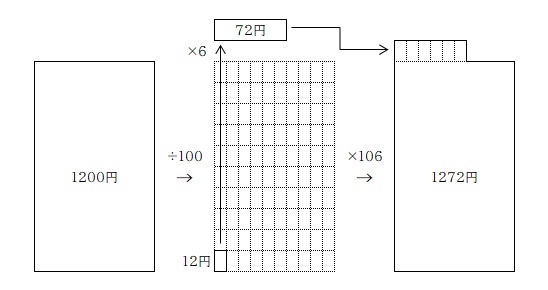
1200円の 6%: 1200×0.06=72円
1200円の 6%増(106%): 1200×1.06=1272円
身近なものなら消費税が同じように計算できますので、いろいろ試してみてください。
さぁ!割合の計算について「なるほど!」って思える勉強はできましたか?
理解できたと思えたなら問題の続きにチャレンジしてみましょう。

今年度の男子と女子の数を文字を使った数式で表してみましょう。
Let's think!
昨年度の男子の人数が x人で今年度は 4%減ということは、昨年度の人数を 100% としたときに今年度の人数は 96% になった、ということ。
x人の 100分の 96 なので、0.96x と表すことができます。
昨年度の女子の人数が y人で今年度は 6%増ということは、昨年度の人数を 100% としたときに今年度の人数は 106% になった、ということ。
y人の 100分の 106 なので、1.06y と表すことができます。

最後に、男子と女子の数の和が合計になるので、

これで方程式がふたつ完成したので連立方程式で解くことができますね。あとは計算だけですが、せっかくなのでやってみてください。
Let's think!
計算の途中で、計算を楽にするポイントもあったりするので説明していきます。

加減法で解いていきます。まずは②の式を100倍して少数をなくします。

次に①の式を 96倍して、②´の式と x の項を揃えます。

ここで計算をちょっと楽にする方法を。
650×96
ここの計算、生徒のノートを見るとたいていは真面目に筆算で計算しているのだけれど少し工夫すると暗算で簡単にできちゃいます。
96 をそのまま使うのではなく 96 = (100-4) に変形して計算してみましょう。
そうすれば、
650×96
↓
650×100=65000
650×4=2600
65000-2600=62400
というように暗算でもできる簡単な計算3つで終わらせることができます。650 と 96 の掛け算を暗算でするのはちょっとしんどいですよね。
ぜひ取り入れて実践してみてください。
さて、計算の続き。②´の式から①´の式を引いて y を求める。
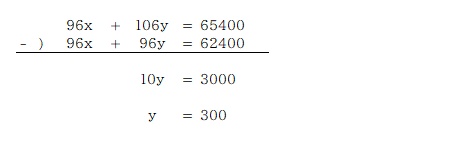
y を①の式に代入し x を求める。

A. 昨年度の男子:350人、女子:300人
数学の文章問題って苦手な子が多いけど、提示された情報をきちんと整理し理詰めで考えれば実はそこまで難しことではないと思っています。
この問題の場合、割合の計算が分からない、なんて子も多いかもしれませんが、そこもきちんと理解し、何度も実践して自在に扱えるようにしてしまえば何てことはありません。
分からないことをほったらかして逃げずに、ちゃんと分かるまで考えて自分のものにしようとする努力をしていきましょう。
----
最後におまけ。連立方程式を使わず解く考え方について。

連立方程式ではないので使う記号はひとつだけ。昨年度男子の数を x とします。男女の合計が 650人だから女子の数を 650-x というように表すことができますね。あとはそれらの数式から今年度の人数を表す数式を書いてあげれば完成。方程式③を解くだけです。
ちなみにこれって、
式① x+y=650 を変形、y=650-x とし、式②に代入している
ということ。つまり連立方程式を代入法で解いているのと同じことなんですよね。違いは、式をふたつ作ってから代入するか、式を作るときに代入した形のものを作るか。
そう考えると実は1年生の方程式の問題を解いているときすでに、連立方程式の代入法のようなことをやって問題を解いていたんですね。
色々考えてみると新しい発見が見つかって面白いかもしれませんね。
問題を解けば終わり、答えが分かれば終わり、ではなく、問題を解く過程でたくさんの「なんだろう?」っていう疑問を見つけて、それを理解していく努力が勉強です。
そしてその「なんだろう?」を解き明かしたときの達成感を味わうのが勉強の醍醐味です!
ぜひたくさんの「分からない」を見つけて、それを「分かった!」に変えていく努力をしていってくださいね!
以上です。お疲れさまでした!
(*ᴗˬᴗ)⁾⁾
2022年
6月
17日
金
「分からない」を考えよう! #8
生徒たちの「分からない」を取り上げて考えていきます。
解き方が分からない前提で「どんな風に考えて解いていくか」という過程を書いていくので、ぜひご自身でも解き方を考えながら読み進めてみてください。
今回は、とある中学のワークからの出題、数学(2年 連立方程式) の問題です。
問題

この問題は、連立方程式の章の中で出題されていた問題です。問題の中にある「解が無数にある」と「解なし」を理解するのにどうすればいいかを色々と考えていました。
多分、それを理解しようとするなら一次関数のグラフに式の線を書いて考えるのが分かりやすいのではないか、と思うのですが、この問題が出題された時点では当然まだ一次関数を学んではいないので、「解・無数」と「解・なし」を理解するのはなかなか難しいかもしれませんね。
まぁ、それは一旦置いておいて、まずはチャレンジ!
Let's think!
さて、どういうふうに進めるか。
いろいろ考えたのだけれど、とりあえず解答・解説を見てみましょうか。
解答・解説

この解説を読んで理解できるかどうか、です。
問題を解くときに「解答を見る」というのはダメなこと、悪いこと、そういうイメージがあるかもしれないですが、きちんと理解するためのアプローチとしては「解答を見る」のは全然アリです。
「解答を見る」ことがダメなのではなく、
「解答を見て、答えを写して終わらせる」ことがダメなのです。
解答を見てからが勉強です。
解答を見て、問題を解く考え方を理解しようする努力をしているかどうか。
勉強ができる子と、できない子の差が付くポイントのひとつです。
勉強ができる側に立ちたい!と思うのならぜひ実践してください。
さて、言いたいこと言うのに話が逸れましたね。
正直私はこの解説を読んできちんと理解できる子は、あんまりいないんじゃないかなぁ、と思います。
けれど、とりあえずは考えてみてください。
Let's think!
それでは、連立方程式の「解・無数」と「解・なし」について、どういうことなのか。どう理解すればいいのか、考えていきましょう。
少しズルい気もしますが、連立方程式の勉強をしている時点ではまだ勉強していない一次関数の知識を使って解説していきたいと思います。
なので、この記事を読んでいる時点で「まだ一次関数の勉強をしていない」子は、一次関数の勉強をしてから読み直してみると分かりやすいかもしれません。
-----
一次関数では、
y = ax + b
という形で式を扱います。1年生のときに勉強した比例の式は「y = ax」でしたね。比例の式が原点 (0,0) を通るのに対し、一次関数の式は原点を通りません。
a:傾き
式をグラフに示したときの直線の、文字通り傾きを表しています。
b:切片
式をグラフに示したときの直線の y軸との交点、y軸上の y座標を表しています。
y軸→つまり x座標が 0 です。一次関数の式に x=0 を代入すると、
y = a × 0 + b
y = b
座標が (0,b) となり、切片 b が y軸上の y座標であることが分かりますね。
実際にグラフに書いてみます。
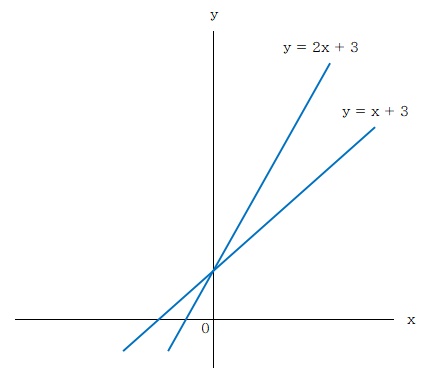
傾き a の値が変われば、直線の傾斜が変わります。
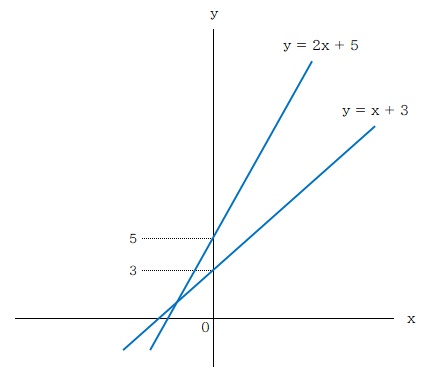
切片 b の値が変われば、y軸との交点の位置が変わります。
ザックリとですがここまでが、一次関数の式とそれをグラフに示したときの直線について、の説明です。
では、ここからは連立方程式の「解・1つ」「解・無数」「解・なし」というがどういうことかを一次関数のグラフに書いて説明します。
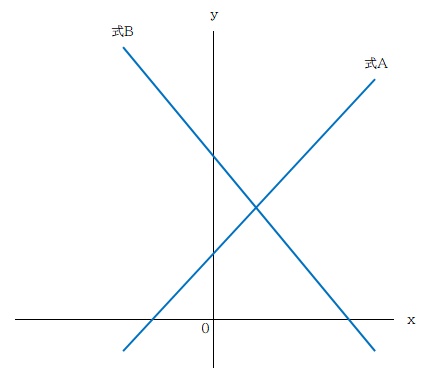
「解・1つ」
連立方程式の解は、ふたつの直線の交点の x座標と y座標を表しています。
一次関数の式の形にしたとき、傾き a の値が異なります。
同じにはなりません。
同じになる場合、というのが次に示す「解・無数」「解・なし」のケースになります。
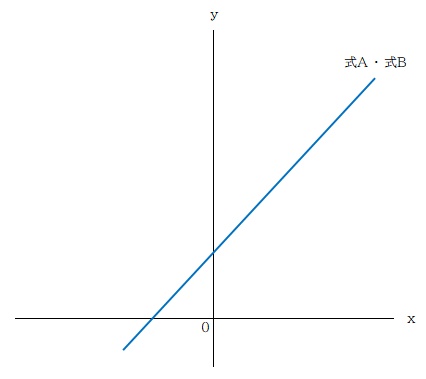
「解・無数」
連立方程式の解は「ふたつの直線の交点」ということでしたね。このようにふたつの直線が完全に重なる場合、ふたつの直線のすべてが交点となり、連立方程式の解が無数にある、ということになります。
一次関数の式の形にしたとき、傾き a の値と切片 b の値がどちらも全く同じ式、ということになりますね。

「解・なし」
連立方程式の解は「ふたつの直線の交点」ですが、このようにふたつの直線が平行になる場合、平行な2直線は決して交わることがないので解がない、ということになります。
一次関数の式の形にしたとき、傾き a の値が等しく、切片 b の値が異なる式、ということになりますね。
どうでしょうか。連立方程式の解について、グラフで示すと「なるほど!」ってなりませんか。多分、分かりやすいと思うのです。
では、ここまで学んだ内容を踏まえこの問題の解を考えてみてください。
Let's think!
それでは問題を解いていきます。
まずはふたつの式を一次関数 y=ax+b の形に直してみましょう。
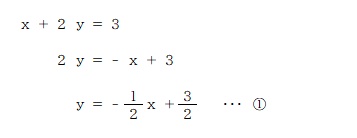
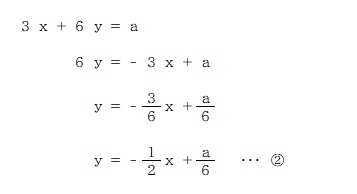
このようになりますね。
まずは、解が無数にある、とはつまり①と②の直線がぴったりと重なる状態ということでした。
傾きは①と②どちらの式も同じす。なので切片が等しくなるような値を考えれば良いですね。
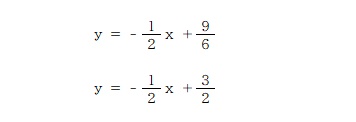
②の式に a=9 を代入してあげると①と同じ式が出来上がります。
よって「解が無数にある」のは a の値が 9 になるとき、ということになります。
そして、解がない、というのは①と②のふたつの直線が平行に並ぶ場合。つまり切片の値が同じにならなければ良いということ。
a=9 で①と②の式の切片の値が同じになる
↓
a=9 以外の値であれば①と②の式の切片の値は同じにならない
よって「解がない」のは a の値が 9 以外になるとき、ということになります。
A. (解が無数にある) a=9 のとき、(解が1つもない) a=9 以外の値をとるとき
いかがでしたか?
この記事を読んで、連立方程式の解が無数にある、解がひとつもない、ということがどういうことか理解できた!という子がひとりでもいてくれたらうれしく思います!
-----
問題を解けば終わり、答えが分かれば終わり、ではなく、問題を解く過程でたくさんの「なんだろう?」っていう疑問を見つけて、それを理解していく努力が勉強です。
そしてその「なんだろう?」を解き明かしたときの達成感を味わうのが勉強の醍醐味です!
ぜひたくさんの「分からない」を見つけて、それを「分かった!」に変えていく努力をしていってくださいね!
以上です。お疲れさまでした!
(*ᴗˬᴗ)⁾⁾
2022年
6月
16日
木
「分からない」を考えよう! #7
生徒たちの「分からない」を取り上げて考えていきます。
解き方が分からない前提で「どんな風に考えて解いていくか」という過程を書いていくので、ぜひご自身でも解き方を考えながら読み進めてみてください。
今回は、とある中学の授業で出されたプリントからの出題、理科(2年 化学) の問題です。
問題

どこかの高校入試の問題の引用らしく、(6) が難しいと言って生徒が持ってきてくれた問題です。
-----
まずは (1) から。この問題は、銅と酸化銅の質量の変化を示した表のデータから計算して求めることができますね。それでは!
Let's think!
(1) の問題。
10.0g の銅を完全に酸素と反応させると何g の酸化銅になるか。表に書かれている銅と酸化銅の質量から比率を求めて、そこに 10.0g を当てはめるとどうなるか、を考えれば良いですね。
表より、銅 0.4g → 酸化銅 0.5g ということが読み取れるので、銅と酸化銅の比率は、
銅:酸化銅 = 0.4:0.5 = 4:5
ということが分かります。あとは比例式にして計算します。
ちなみに比例式の計算の仕方について。「内項の積と外項の積は等しい」という性質から
A:B=C:D → AD=BC
となるのですが、分からない子は調べて勉強しなおしておきましょう。
4:5 = 10.0:x
4x = 50.0
x = 12.5
よって、10.0g の銅を完全に酸素と反応させてできる酸化銅は、
A. (1) 12.5g
ということになります。
-----
それでは (2) に行きましょう!
この問題は、表のデータを使うのと、問題文の中の「銅と酸素は原子数の比が 1:1 で結びつく」ということを合わせて考えれば解を求めることができます。
Let's think!
(2) の問題。
「銅と酸素の質量比」と「銅原子1個と酸素原子1個の質量比」というのはきっちり分けて考えないといけません。この問題の場合は「銅と酸素は原子数の比が 1:1 で結びつく」ということなので、どちらの質量比も同じになるのですが、それもきっちり理解しておきましょう。
まずは「銅と酸素の質量比」について、表のデータから考えます。
銅 0.4g を酸素と完全に反応させてできるのが 0.5g の酸化銅です。ということは、
0.5 - 0.4 = 0.1
銅 0.4g に対して反応した酸素の質量は 0.1g であることが分かります。そこから銅と酸素の質量比は、
銅:酸素 = 4:1
となります。ここから「銅原子1個と酸素原子1個の質量比」を考えます。
「銅と酸素は原子数の比が 1:1 で結びつく」ということは、銅と酸素の原子の数はイコールになるということ。
これはつまり、「銅 0.4g、酸素 0.1g」があったとして、銅の原子数が仮に 100個だとしたら、酸素の原子数も 100個だということ。銅と酸素の質量をそれぞれの原子数で割ると原子1個あたりの質量が分かりますが、
0.4 ÷ 100 = 0.004 ←銅原子1個あたりの質量(仮)
0.1 ÷ 100 = 0.001 ←酸素原子1個あたりの質量(仮)
銅原子1個の質量:酸素原子1個の質量 = 0.004:0.001 = 4:1
というように、原子数の比が 1:1 なら、「銅と酸素の質量比」と「原子1個ずつの質量比」も変わらず同じになるということですね。
よって、「銅原子1個と酸素原子1個の質量比」は、
A. (2) 4:1
となります。
-----
ここからは仮定の話。
もしも、銅と酸素の原子が 1:3 とかで結びつくとしたら?を少しだけ考えてみます。
・「銅原子1個と酸素原子1個の質量比」が 4:1 の場合。
銅と酸素の原子が 1:3 で結びつく、つまり 4:1+1+1 となるので
「銅と酸素の質量比」は 4:3 となる
・「銅と酸素の質量比」が 4:1 の場合。
銅と酸素の原子が 1:3 で結びついている、つまり 4:1/3 + 1/3 + 1/3 となるので
「銅原子1個と酸素原子1個の質量比」は 4:1/3 = 12:1 となる
この理屈が分かるでしょうか。
これがきちんと分かっていれば (6) も解くことができますよ!
-----
それでは (3) に行きましょう!
この問題は、先ほどの問題を解く過程で得た、銅と酸素の質量比、から簡単に解くことができますね。
Let's think!
(3) の問題。
先ほどの問題で、銅と酸素の質量比は、
銅:酸素 = 4:1
であることが分かっていますね。これを使って 6.0g の銅に反応する酸素の質量を求めます。
4:1 = 6.0:x
4x = 6.0
x = 1.5
6.0g の銅に対し反応する酸素の質量は 1.5g であることが分かります。酸素は 6.0g あるとのことですが反応に使われた酸素は 1.5g だけなので 6.0 - 1.5 で、この問題の解は、
A. (3) 酸素が 4.5g 残る
となります。
-----
それでは (4) に行きましょう!
この問題は、反応した酸素の質量、その質量の酸素で反応する銅の質量、を考えていけば解くことができます。
Let's think!
(4) の問題。
3.0g の銅粉を加熱しできた化合物の質量が 3.5g ということは 3.5 - 3.0 で 0.5g の酸素が反応したということが分かります。
銅:酸素 = 4:1
から、酸素 0.5g と反応した銅の質量は、
4:1 = x:0.5
2.0 = x
3.0g のうち 2.0g の銅粉が反応したということなので、まだ反応していない銅の質量は
3.0g - 2.0g だから、
A. (4) 1.0g
となります。
-----
それでは (5) に行きましょう!
この問題は、酸化銅の質量を求める、酸化マグネシウムの質量を求める、マグネシウムと酸素の質量比 3:2 からマグネシウムの質量を考える、という 3つのステップで考えてみてください。
Let's think!
(5) の問題。
銅粉にマグネシウムを混ぜて反応させた、ということだが銅粉は銅粉で分けて考えれば良い。
まずは銅粉 5.0g を完全に酸素と反応させたときの酸化銅の質量を考えます。
銅:酸素 = 4:1
ここまで何度も使ってきた銅と酸素の質量比ですが、扱いやすいように少しパワーアップさせましょう。銅と酸素の比率が 4:1 ということは酸化銅の比率は 5 となりますね。
銅:酸素:酸化銅 = 4:1:5
ここから、銅 5.0g に対する酸化銅の質量を求めます。銅 4 に対して酸化銅 5 なので、
4:5 = 5.0:x
4x = 25.0
x = 6.25
銅粉 5.0g と反応してできた酸化銅は 6.25g であることが分かりました。
酸化銅と酸化マグネシウムの混合物の質量が 8.75g なので、ここから酸化銅の質量を引くと、
8.75 - 6.25 = 2.5
酸化マグネシウムの質量が 2.5g であることが分かりますね。
問題文に「マグネシウムと酸素の質量比は 3:2」であると書いているので、ここから酸化マグネシウムの比率も考えて整理すると、
マグネシウム:酸素:酸化マグネシウム = 3:2:5
マグネシウムと酸化マグネシウムの比率が 3:5 なので、
3:5 = x:2.5
7.5 = 5x
1.5 = x
よって銅粉と混ぜたマグネシウムの質量は、
A. (5) 1.5g
となります。
-----
それでは (6) - ① やってみましょう!
この問題は、酸化銅 22.5g と反応した酸素の質量を求めて考えれば良いですね。
Let's think!
(6) - ① の問題。
酸化物 Y 中の金属 X と酸素の比率を求めよ。で、まず分かっているのが酸化物 Y の質量が 15g だということ。
あとは問題文の中に「酸化銅 22.5g に含まれる酸素と同じ質量の酸素」と反応させた、と記載があるので、酸化銅 22.5g に含まれる酸素の質量を求めればいいですね。
銅:酸素:酸化銅 = 4:1:5
酸素と酸化銅の比率は 1:5 なので、
1:5 = x:22.5
22.5 = 5x
4.5 = x
酸化物 Y の質量 15g のうち、酸素の質量が 4.5g なので、金属 X の質量は、
15 - 4.5 = 10.5
となる。あとは金属 X と酸素の質量比を求めればいいので、
10.5:4.5 = 105:45 = 7:3
よって答えは、
A. (6) - ① 7:3
となります。
-----
それでは (6) - ② やってみましょう!
この問題は、(2) の問題の解と、問題文にある「銅原子と金属 X の原子の質量比」とを合わせて考えてみましょう。
Let's think!
(6) - ② の問題。
問題文に「銅原子1個と金属 X の原子1個の質量比」が「8:7」であると書いてありますね。あとは (2) のところで「銅原子1個と酸素原子1個の質量比」が「4:1」であることも分かっています。
この二つの比率の共通項である「銅原子1個の比率」を揃えてあげれば、金属 X と酸素の原子1個の質量比を求めることができますね。
銅原子1個:金属 X の原子1個 = 8:7
銅原子1個:酸素原子1個 = 4:1 = 8:2
銅と酸素の比率を 2倍にして調整してあげると、銅の比率を揃えることができます。
銅原子の比率「8」に対して、金属 X の原子の比率が「7」
銅原子の比率「8」に対して、酸素原子の比率が「2」
なのだから、
金属 X の原子1個:酸素原子1個 = 7:2
と考えることができますね。よって答えは、
A. (6) - ② 7:2
となります。
-----
それでは (6) - ② やってみましょう!
この問題は、① の比率と ② の比率が異なるという点がポイントです。物質の質量比と、その物質の原子1個の質量比が異なる、ということは原子同士が結びつく個数の比が 1:1 ではないということ。それを踏まえて考えてみてください。
Let's think!
(6) - ③ の問題。
①と②の問題の答えから、
金属 X :酸素 = 7:3
金属 X の原子1個:酸素原子1個 = 7:2
であることが分かっています。原子の質量比と物質の質量比が異なるということは、結びつく原子の個数が異なるということ。
原子の比率 7:2 で、原子の数がいくつといくつで結びつくと物質としての質量比が 7:3 になるのか、を考えれば良いですね。
少し考えやすいように原子の方の比率を少し変形させます。
金属 X の原子1個:酸素原子1個 = 7:2 = 3.5:1
これを物質の質量比 7:3 になるようにすると、
金属 X の原子2個:酸素原子3個 = 3.5 + 3.5:1 + 1 + 1 = 7:3
よって金属 X と酸素の原子数の比は
A. (6) - ③ 2:3
となります。
-----
最後の問題の金属 X ですが、質問をくれた生徒は授業のあとにその正体を友達と一緒に調べてみたそうです。
答えは「鉄」だそう。
酸化鉄の化学式を調べてみると、
酸化鉄(II)、酸化第一鉄:FeO
酸化鉄(III)、酸化第二鉄:Fe₂O₃
酸化鉄(III)鉄(II)、四酸化三鉄:Fe₃O₄
など、さまざまな種類があるようですね。この問題の酸化物 Y というのは酸化鉄(III)ということになるのかな。
中学の勉強の範囲からは逸脱するけれど、興味がある人は調べてみると面白いかもしれないですね。
問題を解けば終わり、答えが分かれば終わり、ではなく、問題を解く過程でたくさんの「なんだろう?」っていう疑問を見つけて、それを理解していく努力が勉強です。
そしてその「なんだろう?」を解き明かしたときの達成感を味わうのが勉強の醍醐味です!
ぜひたくさんの「分からない」を見つけて、それを「分かった!」に変えていく努力をしていってくださいね!
以上です。お疲れさまでした!
(*ᴗˬᴗ)⁾⁾
2022年
6月
13日
月
「分からない」を考えよう! #6
生徒たちの「分からない」を取り上げて考えていきます。
解き方が分からない前提で「どんな風に考えて解いていくか」という過程を書いていくので、ぜひご自身でも解き方を考えながら読み進めてみてください。
今回は、とある中学の「3年 1学期 実力テスト」で出題された、数学の問題です。
問題

(1) は簡単ですね。平均値とは、値の合計を値の数で割ったものです。なので、
(186+182+178+172+168)÷5
=886÷5
=177.2
A. (1) 177.2 cm
となります。ここは簡単。
さて、質問があったのは (2) ですね。この問題は解を考えるときに見落としやすいポイントがある、のかもしれないですね。考えてみてください。
Let's think!
まず、問題文の中にある「メジアン」という言葉。
これは「中央値」のことですね。
ちなみに、なぜ「平均値」は日本語の言葉を使うのに、「中央値」は日本語ではなく英語の言葉を使うのか、が個人的には疑問だったりするのですが、何か理由があるのかな?
まぁ、それは別にいいとして。
中央値 (メジアン) :値を小さい順に並べて、ちょうど中央にある値のこと。
具体例、まずは値の数が奇数のとき。

次は値の数が偶数のとき。

と、中央値はこのように求めます。では中央値について理解したところで問題について考えていきましょう。
d の体重が分からないので、他の 4人の体重を並べてみます。
64 , 72 , 75 , 80
ここのどこかに d の体重 x kg が入るわけですが、x がどこに入ったとしても両端の 64 と 80 が中央値になることはなさそうですね。
中央値となる可能性があるのは 72 か 75、あとは d の体重 x の 3 パターン。
実際に x に色々と数値を当てはめて見ていきましょう。



このように、
「x が 72 以下ならどこに入ったとしても中央値は 72」
「x が 75 以上ならどこに入ったとしても中央値は 75」
であることが分かりますね。あとは、
「x が 72 より大きく 75 未満で中央値は x」
となるパターンです。
よって、中央値として考えられるのは「72 , 75 , x」の 3通り!と考えてしまうと不正解になるので、ここが気を付けなければいけないポイントかな、と思います。
せっかくなので、答えが 3通りだと思ってしまった人は、ここで一度考えてみましょう。
Let's think!
中央値 x を考えるときに気を付けなければいけないポイント、それは、x が取りうる値はひとつだけか?、ということですね。
「x が中央値になる場合」
で考えを止めず、
「x が中央値になる場合、x に当てはまる値は何があるか」
まで考えないとダメですね。
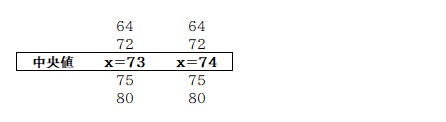
このように x が中央値になる場合、x に当てはまる値は 73 と 74 の 2通りが考えられます。
よって中央値として考えられるのは「72 , 75 , x (73 , 74)」の 4通りとなります。
A. (2) 4通り
分からないと質問があったのはこの問題だけですが、せっかくなのでここでは最後の (3) も考えてみましょう。
Let's think!
まずは、誤った値のままの場合の中央値と、正しい値に基づき修正された中央値 (182) について考えてみます。

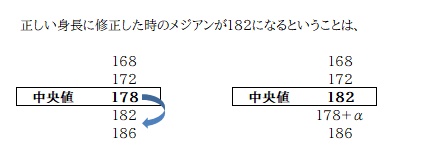
修正前の中央値は 178 で、修正後 182 になったということは、
「168/172/178 のいずれか (おそらく178) が誤りで、正しい数値は 182 より大きい」
ということが考えられますね。
では次に平均値について考えてみます。
(1) の解より 5人の身長の平均値は 177.2 だがこれが誤りで、正しい数値に基づく 5人の身長の平均値は 178.2 となる。
平均値(誤) と 平均値(正) の差は 178.2-177.2=1 なので、5人の平均が 1cm 増えたということは、身長の合計が 5cm 増えたということ。
5人の身長のうち、5cm 増えることで 182 より大きくなるのは、と考えれば答えが分かりますね。
A. (3) 誤っている値 178 cm / 正しい値 183 cm
ちなみに補足。
上記で、誤った値を 168/172/178 のうち 178 がおそらくそうであると考えた理由。
分かりますか?
もし 168 が誤りで正しい数値が 182 より大きくなる場合を考えると、168 だけでなく 172 と 178 も正しい数値が 182 より大きくなる可能性が出てきて、168/172/178 のうちどれが誤った値なのかを特定することができなくなります。
なので正しい平均値から具体的に何 cm 変化があったのかの計算をする前に、誤った値はおそらく 178 かな、と考えたということです。
問題をただ解くだけでなく、問題を解く過程でこんな風にいろいろ考えることが論理的な思考力を養っていくことにつながります。
少しでも楽に解くにはどうすればいいか、だとか、ちょっとの疑問でもトコトン考える!そういう勉強を心がけてください。
-----
問題を解けば終わり、答えが分かれば終わり、ではなく、問題を解く過程でたくさんの「なんだろう?」っていう疑問を見つけて、それを理解していく努力が勉強です。
そしてその「なんだろう?」を解き明かしたときの達成感を味わうのが勉強の醍醐味です!
ぜひたくさんの「分からない」を見つけて、それを「分かった!」に変えていく努力をしていってくださいね!
以上です。お疲れさまでした!
(*ᴗˬᴗ)⁾⁾
2022年
6月
07日
火
「分からない」を考えよう! #5
生徒たちの「分からない」を取り上げて考えていきます。
解き方が分からない前提で「どんな風に考えて解いていくか」という過程を書いていくので、ぜひご自身でも解き方を考えながら読み進めてみてください。
今回は、とある中学の「3年 1学期 実力テスト」で出題された、数学の問題です。
問題

なかなか難問ですね。解き方を知らない問題はワクワクします。解き方を知っていればただの作業ですからね。
それではチャレンジしていきましょう!ご覧の皆様もまずは考えてみてください。
Let's think!
問題文を読んで、書いてあることを正しく理解するだけでも難しい、と感じる子もいるかもしれないですね。
(1) は問題にある [ ] で挟んだ数字が何を意味するのか、問題文を読んでちゃんと理解できたかどうかを確認する問題、といったところでしょうか。
問題として出されているのは [10213] なので、この値を求めるには 10213 を 7 で割ったときの余りを求めればよい、ということになります。
10213 ÷ 7 = 1459 … 0
割り切れましたね。よってこの問題の解は、
A. 0
となります。さて、ここまでは問題の意味が理解できたか、の確認作業。いわば前座のようなもの。次の問題が本番ですよ!
Let's think!
さて、(2) ですが、私の場合はとりあえず数字の小さいものからいくつか計算してみることにしました。2~5乗くらいまでなら計算にさほど時間もかからないと思います。
頭の中だけで考え込むより、考えたことはすぐに手を動かしアウトプットする。トライ&エラーの繰り返しの中から問題を解くためのヒントを見つけ出します。

5乗まで計算してみて、あることに気付きます。余りが 1, 6, 1, 6 と繰り返していますね。これは大きなヒントになる気がしました。
もちろん、たまたまここまでは繰り返しになっているが 6乗の余りは違う数字になるかもしれません。
ですので、今度はこの「余りの 1 と 6 が繰り返していく」という法則が正しいことの証明について考えていく必要がありますね。
その方法の一つに、6乗、7乗、8乗とすべて計算して力ずくで解を見つける、という手段もあるといえばありますが、私はそこまで大きな数の計算はしたくないのでやりません。
というわけで、続きを考えてみてください。
Let's think!
まず、(6の2乗) の余りは 1 です。
これはつまり「(6の2乗)-1」は 7の倍数である、というように言い換えることができます。
(6の2乗)-1
→7の倍数である。7 で割ると 1 余る、ということを表している。
これを元に考えていきます。
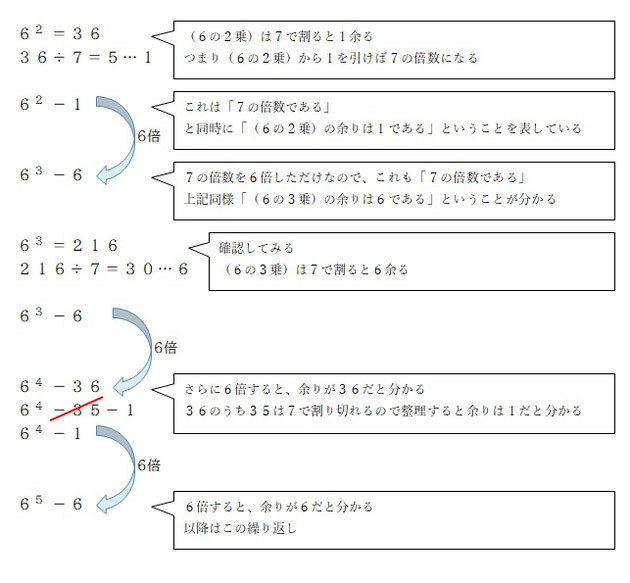
私の場合は、こんな感じで考えをまとめました。
これで、6 の偶数乗の余りは「1」、6 の奇数乗の余りは「6」、であることが証明できたと思います。
よって、6 の x乗のうち、余りが 1 となる 2桁で最小のもの、その解は、
A. x=10
となります。
さて、私なりに考えて、私なりの解き方を書かせていただきましたが、実際どうなんでしょうね。この問題を作られた先生の解説を聞いてみたいです。
もっとシンプルな考え方があるのかもしれません。
これだけのことを考え整理するのにもそれなりの時間がかかりますから、たとえば推測と力技の組み合わせで、
1. 6 の 2~5乗を計算、7で割って余りを求める
2. 余りが 1, 6, 1, 6 続くことから、10乗の余りが 1 になる可能性が高いのではないか、と仮説を立てる。
3. 仮説の実証のため 6 の 10乗を計算し 7 で割って余りを求める
4. 計算を間違えなければ余りは 1 となるので解が x=10 と求めることができる
という解き方でもいいのかもしれません。6 の 10乗の計算にどれだけ時間がかかるかは、やっていないので分かりませんが。
面白い問題だったので是非いろいろ考えてみてください。
ちなみにおまけ。エクセルを使った 6 の x乗の計算結果です。
こういうもの簡単に作ることができます。エクセル、便利ですね。そして、こうして見ると 6 の 10乗くらいなら計算もそこまで苦にはならない気がしますね。
-----
問題を解けば終わり、答えが分かれば終わり、ではなく、問題を解く過程でたくさんの「なんだろう?」っていう疑問を見つけて、それを理解していく努力が勉強です。
そしてその「なんだろう?」を解き明かしたときの達成感を味わうのが勉強の醍醐味です!
ぜひたくさんの「分からない」を見つけて、それを「分かった!」に変えていく努力をしていってくださいね!
以上です。お疲れさまでした!
(*ᴗˬᴗ)⁾⁾
2022年
6月
04日
土
「分からない」を考えよう! #4
生徒たちの「分からない」を取り上げて考えていきます。
解き方が分からない前提で「どんな風に考えて解いていくか」という過程を書いていくので、ぜひご自身でも解き方を考えながら読み進めてみてください。
今回は、とある中学の「2年 1学期 中間テスト」で出題された、理科(1年 地学) の問題です。
問題
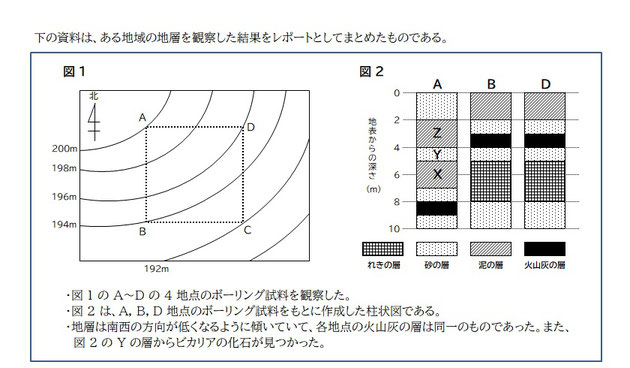

今回は理科の問題。柱状図の読み取りが苦手、というか全然分かってない、っていう子は多いのではないでしょうか。
実はそんなに難しいことではないのでしっかり見直ししていきましょう!とりあえず柱状図の前に、まずは知識を問う設問 (1) と (2) から!
Let's think!
まずは化石についてのおさらい。化石には 2 種類ありましたね。
示相化石 ・・・ 地層ができた当時の「環境」を推定する手がかりとなる化石。
・サンゴ(あたたかくて浅い海)
・ブナ(寒冷な気候)
示準化石 ・・・ 地層ができた「時代」を推定する手がかりとなる化石。
・古生代:フズリナ、三葉虫
・中生代:アンモナイト、恐竜
・新生代:ビカリア、マンモス
ざっくりまとめるとこんな感じでしょうか。これだけ押さえていれば (1) と (2) は簡単に正解することができますね。
A. (1) 示準化石 (2) 新生代
(3) は堆積についてちゃんと分っていないと解くのは難しいですね。当てずっぽうで正解しても意味がないです。答えが何か、が分かっただけでも意味がないです。答えが分かったら、どうしてその答えになるのか、について理解できるまで見直しましょう。
Let's think!
さて、(3) です。柱状図を見ると、
「X」泥の層、「Y」砂の層、「Z」泥の層、
となっていますね。ここから何を読み取ればいいのか。地層がどのように形成されるのか、見ていきましょう。
Step1. 風化:気温の変化・太陽光・氷結・風雨などの影響で、岩石がもろくなる。
Step2. 浸食:雨水や流水によって岩石が削られ土砂となる。
Step3. 運搬:流水によって土砂が運ばれる。
Step4. 堆積:運ばれた土砂(れき、砂、泥)がたまり積み重なっていく。
堆積の仕方
粒の大きなもの:流されにくいため、海岸から近く浅い水底に堆積していく。
粒の小さなもの:流されやすいため、海岸から遠く深い水底に堆積していく。
粒の大きさ: (大) ← れき 砂 泥 → (小)
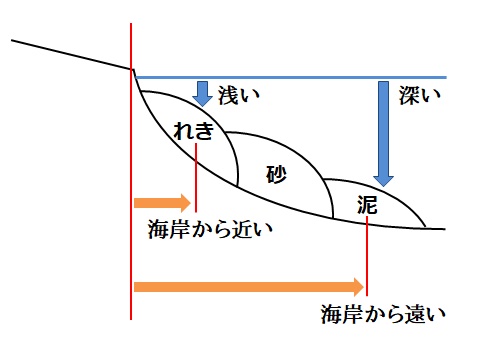
つまり、地層の種類から、
「れきの層」が形成された
→以前の層(下のある層)が、
「砂」「泥」のいずれでも、地面の位置が「高い」場所に移動した(隆起)
「砂の層」が形成された
→以前の層が、
「れき」なら、地面の位置が「低い」場所に移動した(沈降)
「泥」なら、地面の位置が「高い」場所に移動した(隆起)
「泥の層」が形成された
→以前の層が、
「れき」「砂」のいずれでも、地面の位置が「低い」場所に移動した(沈降)
というようなことを読み取ることができるというわけです。
さて、では (3) を見ていきます。ここまできちんと理解していれば解くのは簡単ですね。
地層は古い時代のものから、
「X」泥の層 → 「Y」砂の層 → 「Z」泥の層
の順で形成されているので、
「X」泥の層が形成される、深い場所にあった
「Y」高い場所に移動し(隆起)、砂の層が形成される
「Z」深い場所に戻り(沈降)、泥の層が形成される
地層の形成順序によって以上のように読み解くことができますね。よって答えは、
A. (3) ウ 【隆起してから沈降した】
次の問題は柱状図の読み取りです。柱状図の位置をきちんと揃えて並べてあげる、のがポイントですね。
Let's think!
では (4) を見ていきましょう。
柱状図を見るときに気を付けなければいけないことは、柱状図は全て地表 0 メートルを基準にして揃えられ書かれている」ということです。
図 2 の柱状図、きれいに並べてありますが、図 1 を見ると各地点の地表 0 メートルの標高はバラバラであることが分かりますよね。
ですので柱状図を見るときは、
柱状図の「地表 0 メートル」を、各地点の標高の位置に合わせること
が大切なポイントとなります。地表 0 メートルで揃えられた柱状図を、各地点の標高ごとに並べなおします。
問題の 図1 を見ると標高は、A地点:200m、B地点:194m、D地点196m、です。
それぞれの標高に、柱状図の地表 0m を並べなおすと ↓ のようになりますね。
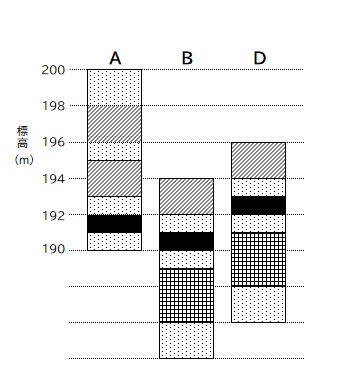
この並べ替えさえできてしまえば、あとはこの図から回答となる情報を読み取るだけ。
A. (4) ① 1 ②192 ③193
さぁ、次で最後の問題です。
Let's think!
(5) は C 地点の火山灰の層の位置を推察する問題ですね。
そのために必要な情報は「地層は南西に傾いている」という点。(4) の問題文の中になる情報を整理し、C 地点と比較をすると。
地層は南が低くなる:A より B が 1m 低い
→ C より北にある D と比較すると、D より C が 1m 低い
地層は西が低くなる:D より A が 1m 低い
→ C より西にある B と比較すると、C より B が 1m 低い
となる。解を求めるには上記のどちらを利用しても構いません。
図に書いて比較してみよう。
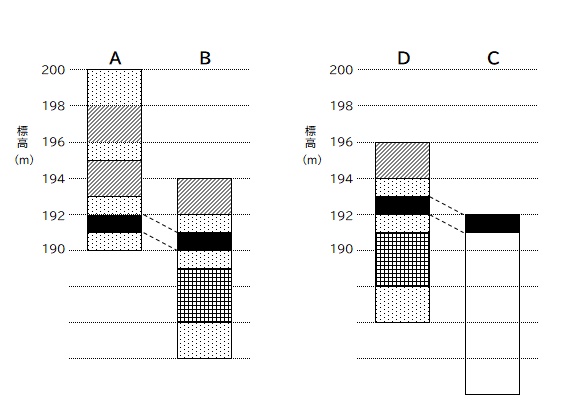
↑↑↑
A 地点と B 地点の火山灰層の高低差をもとに、
D 地点から C 地点の火山灰層の位置を推測する。

↑↑↑
A 地点と D 地点の火山灰層の高低差をもとに、
B 地点から C 地点の火山灰層の位置を推測する。
いずれの方法でも C 地点の火山灰層の位置は同じになりますね。
A. (5) C 地点の火山灰の層は 0~1m の位置 ※回答は上記図の通り
-----
今回も記事を書くのにそれなりに時間をかけ、たくさんのことを調べました。だからこそ、その過程で得た知識が身についていくのです。
知りたいことのために時間をかけること、その中で新たに生まれた「気になること」も時間をかけて調べること。寄り道こそが知識の量と幅を広げる最短の道だったりします。
問題を解けば終わり、答えが分かれば終わり、ではなく、問題を解く過程でたくさんの「なんだろう?」っていう疑問を見つけて、それを理解していく努力が勉強です。
そしてその「なんだろう?」を解き明かしたときの達成感を味わうのが勉強の醍醐味です!
ぜひたくさんの「分からない」を見つけて、それを「分かった!」に変えていく努力をしていってくださいね!
以上です。お疲れさまでした!
(*ᴗˬᴗ)⁾⁾
2022年
6月
02日
木
「分からない」を考えよう! #3
生徒たちの「分からない」を取り上げて考えていきます。
解き方が分からない前提で「どんな風に考えて解いていくか」という過程を書いていくので、ぜひご自身でも解き方を考えながら読み進めてみてください。
今回は、とある中学の「2年 1学期 中間テスト」で出題された、英語(未来の文 be going to/助動詞will、助動詞must、接続詞when/if) の問題です。
問題

特別難しい問題ではありません。テスト範囲で習った文法の並べ替え問題です。
個人的には、私が中学生だったころから好きな問題でした。理由は英単語のスペルを覚えてなくても良いから!、あとパズルみたいで楽しくないですか?
ですが、英語に苦手意識を持っている子は、これがなかなか難しいようで正しく並べなおすことが出来ません。
並べ替え問題は英文法のルールに基づいた「英単語並べ替えパズル」のようなものなので、ラッキー問題だと思えるようにしっかりと考えられるようになって欲しいですね。
それでは (1) の問題から。
Let's think!
(1) あなたは何時に寝るつもりですか。
( you / what time / to / are / going / do / go to bed / ? )
まずこれは未来の予定について質問している文ですね。なので文法は、
be going to + 動詞の原形
となります。「寝る」は go to bed なので、
are going to go to bed ( you / what time / do / ? )
こんな感じで分かるところから文の塊を作っていくと分かりやすいかもしれないですね。次にこの文の主語は「あなた」なので文の先頭に持ってきますが、疑問文なので be動詞と入れ替えないとダメですね。
are you going to go to bed ( what time / do / ? )
あとは連語の疑問詞 what time ですが、疑問詞の疑問文は疑問詞を先頭に置けばいいですね。最後に ? を付ければ完成です。
A. What time are you going to go to bed ? ( do )
「未来の文 be going to / be動詞の疑問文 / 疑問詞の位置」
押さえておくべき文法はこれだけかな。よく分かってない子は見直しておきましょう。
では次の問題。
Let's think!
(2) 明日、晴れることを望みます。
( I / it / hope / will / is / clear / be / tomorrow / . )
まずこの文の動詞は「望みます」です。では誰が「望む」のか?「望んでいる」のは「私」だと考えられるので、日本語の文では省略されていますが、主語は「私」ですね。なので主語と動詞はセットにできますね。
I hope ( it / will / is / clear / be / tomorrow / . )
時間を表す副詞 tomorrow は基本的には文の最後に置けばよいので、
I hope ・・・ tomorrow . ( it / will / is / clear / be )
あとは天気の部分。天気の表現は、
it is + 天気を表す形容詞
となり、「晴れ」を表す形容詞は clear だから天気の表現は「it is clear」。
さらにここでは明日、つまり未来の天気の話なので will も組み込み「it will is clear」。
助動詞 will のあとにくる動詞は原型なので「it will be clear」。よって、
A. I hope it will be clear tomorrow . ( is )
「未来の文 will / 天気の表現 / 時間を表す副詞の位置」
押さえておくべき文法はこれだけかな。よく分かってない子は見直しておきましょう。
では次の問題。
Let's think!
(3) 真央は 6 時までに宿題をしなければなりません。
( Mao / do / by / hers / homework / must / six o'clock / her / . )
まずは「真央は宿題をする」という文を考えてみましょう。英語だと「真央は、する、宿題を」という並びになりますね。
「する」は do
「宿題」は homework
ここで注意しないといけないのは、英語では「誰の宿題」なのかをはっきりさせます。真央は他の誰かの宿題をするわけではなく、自分の宿題をするわけですよね。なので、英語の文では「彼女の宿題」と書かないとダメなんですね。日本語の文には書かれることがないので見落としやすいポイントです。なので
「宿題」は her homework
ちなみに hers の方は所有代名詞で「彼女のもの」という意味なのでここでは使いません。
Mao do her homework ( by / hers / must / six o'clock / . )
この時点だと文法的におかしな箇所がありますね。分かりますか?主語の Mao は三人称単数、この文の時制は現在なので動詞 do には三単現の s を付けて does にしないといけません。
なのですが、この問題の文は「しなければならない」、つまり助動詞 must を使う文だから動詞の do は原型のままで良いというわけですね。
Mao must do her homework ( by / hers / six o'clock / . )
あとは「6時までに」の部分。前置詞 by が「~までに」、「6時」は分かりますよね。時間を表す文は文の最後に持ってくるので、
A. Mao must do her homework by six o'clock . ( hers )
「助動詞 must / 所有格の代名詞 / 時間を表す文の位置」
押さえておくべき文法はこれだけかな。よく分かってない子は見直しておきましょう。
では次の問題。
Let's think!
(4) 私は日本にいたとき、ときどき釣りを楽しみました。
( I / sometimes / fishing / when / if / I / enjoyed / was / in Japan / . )
~したとき、~した。これは接続詞 when で繋ぐ文ですね。まぁとりあえず、「私は日本にいた」「釣りを楽しみました」の二つの文を考えてみましょう。
「私は日本にいた」
be動詞の文は二種類あって、
「○○は△△だ」というように状態を表すもの。
「○○は□□にいる」というように存在を表すもの。
後者は be動詞のあとに場所を表す言葉が入ります。あと、この文は過去形なので、次のように並べればいいですね。
I was in Japan ( sometimes / fishing / when / if / I / enjoyed / . )
「釣りを楽しみました」
これは主語が省略されていますが、釣りを楽しんだのは「私」ですよね。釣りは fishing 、楽しむは enjoy なので、
I was in Japan / I enjoyed fishing ( sometimes / when / if / . )
ここまでを見てみると、簡単な be動詞の文と一般動詞の文だけですよね。これなら分かる!って思えませんか?
さて次は「釣りを楽しみました」に「ときどき」を追加します。
「ときどき」は sometimes 、頻度を表す副詞です。頻度を表す副詞は基本的には一般動詞の前に置きます。
I was in Japan / I sometimes enjoyed fishing ( when / if / . )
完成まであと少しです。~したとき、という文なので使うのはもちろん when ですね。「日本にいたとき」なので I was in Japan の前に置きます。
when I was in Japan / I sometimes enjoyed fishing ( if / . )
最後に考えないといけないのはこの二つの文の並べ方です。
when を含む文節を前に置いた場合は、後半の文との間を ,(カンマ) で区切るのが通例です。
when を含む文節を後に置いた場合は、カンマで区切る必要はありません。
この問題で用意されている単語の中にカンマは無いので、when の文節は後に置きましょう。
A. I sometimes enjoyed fishing when I was in Japan . ( if )
「存在を表す be動詞の文 / 接続詞 when / 頻度を表す副詞の位置」
押さえておくべき文法はこれだけかな。よく分かってない子は見直しておきましょう。
では次の問題。
Let's think!
(5) もし舞が私の家に来るのなら、私はケーキを作ります。
( comes / my house / make / if / to / I / Mai / when / will / a cake / , / . )
もし~なら、~する。これは接続詞 if で繋ぐ文ですね。先ほどの問題と同様に二つの文をつなげた形になります。ですので今回も、「舞が私の家に来る」「私はケーキを作ります」の二つに分けて考えてみましょう。
「舞が私の家に来る」
シンプルな一般動詞の文ですね。日本語を英語風に並べ替えるなら「舞が、来る、私の家に」となりますが、英語が苦手な子はまず日本語の方を並べ替えてみると分かりやすいかもしれませんね。場所を表す言葉の前に前置詞 to を置いて「~に」を足すのも忘れずに。
Mai comes to my house ( make / if / I / when / will / a cake / , / . )
「私はケーキを作ります」
これも一般動詞の文ですね。日本語を英語風に並べ替えるなら「私は、作る、ケーキを」となります。ただ、気を付けないといけないのは「ケーキを作る」のは「舞が家に来たら」という未来のお話だということ。なのでこちらの文には未来を表す助動詞 will が必要になります。
ちなみに、「舞が家に来たら」の方の文も未来の話ですが、こちらは「もし~ならば」という if に続く副詞節は現在の文として書きます。
Mai comes to my house / I will make a cake ( if / when / , / . )
あとは接続詞 if で二つの文をつなげます。if を置くのは「舞が私の家に来る」の文の前、そしてこの並べ替えの単語の選択肢には ,(カンマ) が用意されているので、if の文節を前に置いて後半の文との間をカンマで区切れば ok です!
A. If Mai comes to my house , I will make a cake . ( when )
「接続詞 if / 前置詞 to / 二つの文節の時制の違い」
押さえておくべき文法はこれだけかな。よく分かってない子は見直しておきましょう。
-----
一見簡単そうに見える並べ替えの問題ですが、本気で勉強しようと思ったらかなりたくさんのことを学べた気がします。
ここまで書くのに、実はたくさん寄り道をしています。
① will と be going to の違い
will :
その場で決まったこと(発言する前は決まっていなかったこと)について話す際に使われる。未来、というより未来に対する意思表示のニュアンス。
be going to :
既に予定していたことや、計画していたことについて話す際に使われる。
② 「晴れる」の表現 sunny, fine, clear
sunny :さんさんと太陽の光が降り注ぐ様子を表す。
fine :気持ちのいい日、というニュアンス。少々曇っていても使われる。
clear :雲がなく澄み切った状態。快晴。
③ 頻度を表す副詞 always, usually, often, sometimes, never
置く位置:
一般動詞の前、be動詞の後ろ、助動詞 (can, will など) がある場合は助動詞と動詞の間。
→否定文を作る時の not と同じ位置、と覚えておくと分かりやすい。
どれくらいの頻度のときに使うの?:
always:いつも(100%)
usually:たいてい、普通(80%)
often:よく、しばしば(60-70%)
sometimes:時々(40-50%)
never:決して〜ない(0%)
※パーセンテージはあくまで目安。話し手の主観による。頻度の多い少ないの順番としてこの並びの通り。中学で覚えておくのはこの 5 つくらいでいいと思う。
④ 接続詞 when, if(並べる順番)
接続詞を含む文節は、前においても後ろにおいてもどちらでも良い。前に置く場合は、後ろの文との間をカンマで区切る。
When<文A>, <文B>.
<文B> when<文A>.
If<文A>, <文B>.
<文B> if<文A>.
⑤ 接続詞 when, if(時制の違い)
when と if を使った副詞節の文は未来のことでも現在形を使う。つまり、
When<文A(現在形)>, <文B(Will)>.
If<文A(現在形)>, <文B(Will)>.
となる。この形になった理由は諸説あり、その中の一つに、
will とは「意志」や「予想」という、「心の動き」を表すために使う言葉。
「~するとき」「~ならば」といった時や条件には人の意志は介在しません。だから、そもそも「心の動き」を表す助動詞 will を使う必要がない、という説があるそうです。
理由が、なるほどな、と思えるものだったので、いくつかの中からこの説を紹介しました。
などなど、挙げればキリがないのですが細かいことが気になって、この記事一本書くために本当にたくさんのことを調べました。知らないこと、忘れていたことも色々あってすごく楽しかったです。
問題を解けば終わり、答えが分かれば終わり、ではなく、問題を解く過程でたくさんの「なんだろう?」っていう疑問を見つけて、それを理解していく努力が勉強です。
そしてその「なんだろう?」を解き明かしたときの達成感を味わうのが勉強の醍醐味です!
ぜひたくさんの「分からない」を見つけて、それを「分かった!」に変えていく努力をしていってくださいね!
以上です。お疲れさまでした!
(*ᴗˬᴗ)⁾⁾
2022年
5月
31日
火
「分からない」を考えよう! #2
生徒たちの「分からない」を取り上げて考えていきます。
解き方が分からない前提で「どんな風に考えて解いていくか」という過程を書いていくので、ぜひご自身でも解き方を考えながら読み進めてみてください。
今回は、とある中学の「2年 1学期 中間テスト」で出題された、数学(式の計算) の問題です。
問題
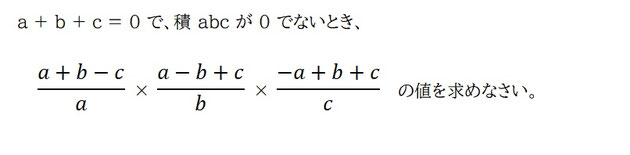
今回のテスト問題を見た中で個人的に「一番面白そう!」と思った問題です。ちなみに、その生徒のクラスで正解できたのは3人だけだったそうです。
さて、一番面白そう、と思った理由はパッと見て解き方が分からなかったから!
なのでワクワクしながら挑戦スタートです。
まず、解き方は分からない、が、上手いこと式を整理してあげれば良いんだろうな、ということは分かっていました。問題はどういう整理の仕方をするか、ですね。
こういうときは、
(1) とりあえずこの問題は飛ばして解ける問題を解いていく。
(2) とりあえずできる計算をやってみる。
その過程でこの問題を解くヒントが見つかるかもしれません。私はとりあえず、そのまま計算してみました。頭の中だけで考え込むより、まずは手を動かすのが性に合っています。
Let's think!
とりあえず計算してみたら、いろいろ打ち消しあっていい感じに整理されたら良いなー、と思いつつ、一方では多分これじゃ無理だろうなー、とも思いながら計算してみました。
計算しつつも、頭の中では式を整理するための工夫を考えながら。
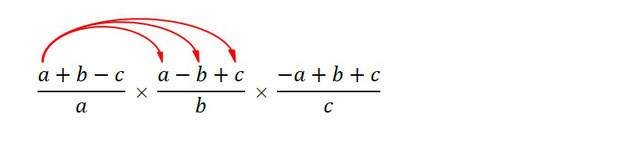
こんな感じで、本当にただ計算して整理してみます。

ここまで計算してみましたが、赤丸の同類項を整理してもこれ以上はどうにもならなそうですね。そもそもこの計算をするだけで時間がかかり過ぎていて、時間制限のあるテストの中ではこんなことをしている余裕はないでしょう。
正面突破は無理、ということが分かりました。
そこで問題文を最初から見直すと、そういえばもう一つ式あるよね、ということに気づきます。
a+b+c=0
実はこの式こそが問題を解くためのカギ!問題の式の中に a+b+c があれば 0 を代入することができます。ですが、問題の数式の分子の部分には、
a+b-c 、a-b+c 、-a+b+c
というように、どれもマイナスが入っていて代入することができません。マイナスの項が邪魔です。なので、ちょっと整理してみました。
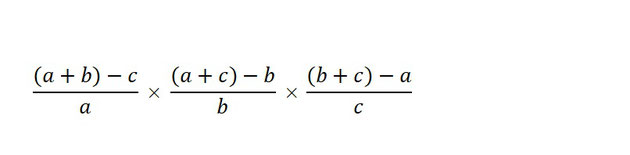
私の場合はここでピンときました。
a+b+c を代入できる個所は無い、けれど a+b だけなら代入できそうです。a+c 、b+c も同様です。
問題を解くためのカギ(a+b+c=0)はある。でもこのままでは問題のカギ穴には合わない。じゃあカギの形のほうを変えてしまえば。さて、それでは、
Let's think!
問題文にある a+b+c=0 を次のように変形させます。
a + b = -c
a + c = -b
b + c = -a
この形であれば代入して計算していくことができますね。
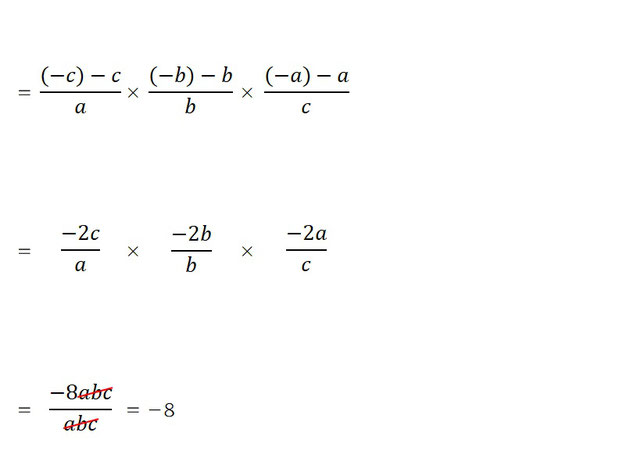
A. -8
キレイに整理され解くことができましたね。
-----
問題を解けば終わり、答えが分かれば終わり、ではなく、問題を解く過程でたくさんの「なんだろう?」っていう疑問を見つけて、それを理解していく努力が勉強です。
そしてその「なんだろう?」を解き明かしたときの達成感を味わうのが勉強の醍醐味です!
ぜひたくさんの「分からない」を見つけて、それを「分かった!」に変えていく努力をしていってくださいね!
以上です。お疲れさまでした!
(*ᴗˬᴗ)⁾⁾
2022年
5月
30日
月
「分からない」を考えよう! #1
生徒たちの「分からない」を取り上げて考えていきます。
解き方が分からない前提で「どんな風に考えて解いていくか」という過程を書いていくので、ぜひご自身でも解き方を考えながら読み進めてみてください。
今回は、とある中学の「2年 1学期 中間テスト」で出題された、数学(式の計算) の問題です。
【問題】

表の中の数字 N を、その数字の位置を表す座標 x,y の値から求める式を考えれば良いんだな、みたいなことをまず考えることができればいいですね。
そこでまずは数字の変化に規則性はないか、探してみましょう。
Let's think!
数字の変化の規則性、見つけることができましたか?
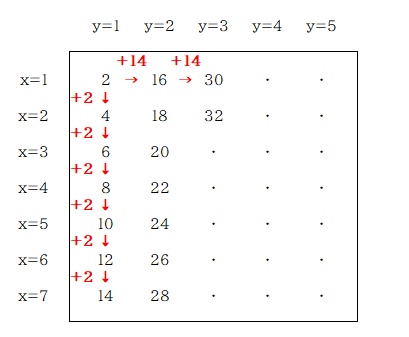
数字は偶数が順に並んだものなので 2 ずつ増えていきます。1つの列に 7つ並べたところで次の列に移ります。なので横の数字を見ると 14 ずつ増えているのが分かりますね。
では、この規則的な変化を x と y を使って表す数式を作っていきましょう。
Let's think!
まず縦方向の数式は簡単に思いつくと思います。

x=1 のときが 2 で、そこから x が 1 増えるごとに 2 ずつ増えていくので、シンプルに 2x という式が成立しますね。
ではさらに横の変化、y を絡めた式を作りましょう。

ヒントその1、です。
1行目だけを見て考えてみます。2、16、30、という数字を先に考えた 2x と合わせて作ることができればいい。1行目なので 2x に x=1 を代入し 2x=2 となります。
よって、横の数字を「x を使って求める数」と「y を使って求める数」に分けると、
2+0 、2+14 、2+28 と表すことができますね。
この 0 、14 、28 の部分を、y の値を使って求める式を作っていきます。
Let's think!
y を使った数式を作ることができましたか?できなかった人のためのヒントその2、です。

「2x+〇〇」の ○○ の部分を少し分解して考えてみます。
最初に変化の規則性を考えたときに、横の数字は 14 ずつ増えていると考えたのを思い出してみましょう。
14 の個数がいくつになるか、を考え、その個数を求める式を y の値を使って求める数式を考えるようにすると、すごく分かりやすくなったと思いませんか?
整理すると、
「2x+〇〇」の ○○ の部分を求める数式を考える
↓
「2x+(14×〇〇)」の ○○ の部分を求める数式を考える
ということになりますね。では、最後です。y の値を使って 〇〇 の部分を求める数式を作ってみましょう。
Let's think!
「2x+(14×〇〇)」の ○○ の部分、14 の個数を求める部分の数式は、
y=1 のとき 0 、y=2 のとき 1 、y=3 のとき 2
となる。つまり「y の値より 1 小さい数」ということが分かるので y-1 とすれば求めることができますね。
よって N を求めるための数式、その答えはこのようになります。
N = 2x + 14(y-1)
では、これが正しいか確認です。問題文にある N(3,2) を代入して解が 20 になるかどうか。他にも適当に N(5,2) とか N(1,3) とか試してその位置の値を求めることができれば ok ですね。
この数式さえ完成してしまえばあとは簡単。
(1) N(3,5) を代入して値を求める。
(2) x=1 を代入して式を整理する。
Let's think!
(1) N(3,5) を代入して値を求める。
N = 2x + 14(y-1)
N = 2×3 + 14(5-1)
N = 6 + 14×4
N = 6 + 56
N = 62
A. 62
-----
(2) x=1 を代入して式を整理する。
N = 2×1 + 14(y-1)
N = 2 + 14y - 14
N = 14y - 12
A. N = 14y - 12
ちなみに、この問題の答えの数式が何を表すものなのか?っていうのは分かりますか?
この式は「1行目限定で y 列目の値を求める数式」です。
-----
問題を解けば終わり、答えが分かれば終わり、ではなく、問題を解く過程でたくさんの「なんだろう?」っていう疑問を見つけて、それを理解していく努力が勉強です。
そしてその「なんだろう?」を解き明かしたときの達成感を味わうのが勉強の醍醐味です!
ぜひたくさんの「分からない」を見つけて、それを「分かった!」に変えていく努力をしていってくださいね!
以上です。お疲れさまでした!
(*ᴗˬᴗ)⁾⁾
2019年
11月
03日
日
文章問題の考え方講座 ~part5~
今回は連立方程式の範囲の問題です。
式を解くのに必要なのは連立方程式の知識ですが、式を立てるのに必要なのは「時間」「角度」「単位量あたりの数」あたりの考え方でしょうか。
では、問題がこちら。
------------------------------------------------
7時x分 の長針と短針の位置が、2時y分 で入れかわるとき
(1) x と y についての連立方程式を立てなさい。
(2) x の値を求めなさい。
------------------------------------------------
まずは問題における「7時x分の長針と短針の位置が、2時y分で入れかわる」というのが、どういう状態なのか。ここをきちんと理解し、イメージできなければダメですね。
長針と短針の位置が「7時x分」と「2時y分」で入れかわるということは、
短針(時間を示す針)の位置が、
「7時x分」→「7」と「8」の間
「2時y分」→「2」と「3」の間
となるので、
長針(分を示す針)の位置は、
「7時x分」→「2時y分」における長針の位置、つまり「2」と「3」の間
「2時y分」→「7時x分」における長針の位置、つまり「7」と「8」の間
となりますね。

図にするとこんな感じです。
「7時x分の長針」と「2時y分の短針」
「7時x分の短針」と「2時y分の長針」
がそれぞれ等しい位置にあるということですね。
あとはそれぞれの位置を数式で表すことができれば等式を二つ書くことが可能です。
で、長針と短針の位置を表わすのに用いるのが角度。
「12」の位置、つまり 0時を起点として長針および短針の位置までの角度を「x分」「y分」を使って表わすことができないか?
という発想に辿り着けばあとは簡単。

まずは長針の角度を考えます。
長針は 60分で 1周 (360°) 回るので、
360÷60=6
長針が 1分あたりに動く角度は 6° です。なので、
7時x分 の長針の角度は「6x」
2時y分 の長針の角度は「6y」
と表すことが出来ます。

次に短針の角度。
短針は 60分で時計の数字1つ分、つまり 1時間あたり (30°) 動くので、
30÷60=1/2
短針が 1分あたりに動く角度は 1/2° です。なので、
7時から x分 経ったときの短針の角度は「1/2x」
2時から y分 経ったときの短針の角度は「1/2y」
と表すことが出来ます。
ただし、短針は 0時からの角度も考えないといけません。

短針は 1時間あたり (30°) だから、
0時から 7時までの角度は「210°」
0時から 2時までの角度は「60°」
です。ここは簡単ですね。

あとは、
「0時 から 7時 の角度」と「7時 から 7時x分 の角度」
「0時 から 2時 の角度」と「2時 から 2時y分 の角度」
を足したものが、0時を起点とした短針の角度となります。なので、
7時x分 の短針の角度は「1/2x + 210」
2時y分 の短針の角度は「1/2y + 60」
と表すことが出来ます。
最後に、ここまでで作った「長針と短針を表わす数式」をイコールの関係にあるもの同士まとめれば完成です。

7時x分の短針の角度 = 2時y分の長針の角度
1/2x + 210 = 6y

7時x分の長針の角度 = 2時y分の短針の角度
6x = 1/2y + 60
これで (1) の問題は終了。
(2) の問題はこの2つの式を連立方程式で解くだけですね。
以上、今回の問題、解説はいかがでしたか?
中学生の皆さんは、読んでみて終わり、ではなく、ぜひ同じ問題を自分でも実際に解いてみて下さい。
実際に解いてみると、読んでいた時には気づかなかった疑問や、よく分からないことなどが見えてくることもありますので(^^)
2019年
10月
27日
日
文章問題の考え方講座 ~part4 #2~

右の図のように、
直線①:y=x/2
双曲線②:xy=6 (x>0)
2点 A(-4,3) B(-1,-1)
がある。
また、四角形ABCDが平行四辺形となるように、2点 C , D をそれぞれ①、②の上にとる。次の問いに答えなさい。
(1) 2点 C , D の座標をそれぞれ求めなさい。
(2) 点P (3,-1) を通る直線n で、平行四辺形ABCDの面積を2等分したい。
直線n の式を求めよ。
--------------------------------------------------
前回は、
「平行四辺形ABCD の中心(対角線の交点)を軸にして、点P と点対称になる点」
について考え、その点と 点P を結ぶ直線を求めました。
ちなみに、
「この直線がどうして 平行四辺形ABCD の面積を二等分する線になるのか?」というと、
点対称になる点同士を結ぶ
↓
点対称の中心を通る
↓
点対称の中心は、平行四辺形ABCD の中心(対角線の交点)
となり、「平行四辺形の中心を通るから」が答えですね。
平行四辺形を二等分する直線 = その平行四辺形の中心(対角線の交点)を通る直線
今回はこの考え方で問題を解いていきたいと思います。
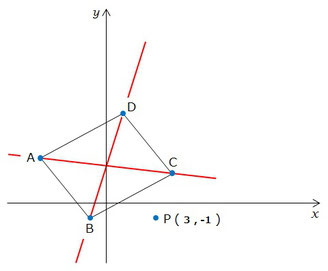
まずは 平行四辺形ABCD の対角線の式を求めていきます。
(1) の問題を解いていれば 点A ~ 点D の座標は全部分かっているはずなので、
点A と 点C の座標から 直線AC の式を求める
点B と 点D の座標から 直線BD の式を求める
一次関数の式 y=ax+b にそれぞれの座標を代入して連立方程式で解けば良いですね。

直線AC と 直線BD の交点の座標を求める
この座標が対角線の交点、つまり 平行四辺形ABCD の中心ですね。

最後に、
平行四辺形ABCD の中心の点 と 点P を結ぶ 直線n の式を求める
となります。
前回の解き方よりかなり手順が多いですね。全部で連立方程式を4回も解かないといけません。と、考えると面倒なだけのように思うかもしれませんが、「入試に向け連立方程式の計算の復習も出来る」と捉えればこちらの解き方を選ぶことにも価値が生まれますね。
全ては捉え方次第。
ぜひ色々な考え方で問題を解き数学を楽しんでください(^^)
2019年
10月
26日
土
文章問題の考え方講座 ~part4 #1~
前回(part3 #2)の続き。
今回は (2) の問題について考えていきます。
解説するのが (1) から (2) の問題に変わるので part も新しくしますね。
-------------------------------------------------

右の図のように、
直線①:y=x/2
双曲線②:xy=6 (x>0)
2点 A(-4,3) B(-1,-1)
がある。
また、四角形ABCDが平行四辺形となるように、2点 C , D をそれぞれ①、②の上にとる。次の問いに答えなさい。
(1) 2点 C , D の座標をそれぞれ求めなさい。
(2) 点P (3,-1) を通る直線n で、平行四辺形ABCDの面積を2等分したい。
直線n の式を求めよ。
--------------------------------------------------
グラフに 点P を追加するとこんな感じですね。

平行四辺形ABCD の面積を半分にする直線、なので、
「平行四辺形ABCD の中心(対角線の交点)を軸にして、点P と点対称になる点」
を求めて、点P と結べば二等分に出来ますね。
点P と点対称な点を「点Q」とします。
点Q は、「点P が 点B からどれだけ移動した場所にあるか」という位置情報をもとに、「点D (点B と点対称な点) から逆向きに同じだけ移動した場所」を考えることで求めることが出来ますね。

点P は 点B から「x軸プラス方向に 4」移動した位置にあることが分かるので、点D から「x軸マイナス方向に 4」移動した位置に 点Q を作れば良いですね。

(1) の問題が解けていれば 点D の座標はすでに計算済みのはずですので、そこから 点Q の座標も求めることが出来ます。
あとは 点P / 点Q の座標を y=ax+b にそれぞれ代入し、連立方程式を解いて a / b の値を求めれば 直線n の式の完成ですね。

さて、今回の解説もきちんと伝わったでしょうか?
次回はこの問題を別のアプローチで解いていきたいと思います(^^)
2019年
10月
25日
金
文章問題の考え方講座 ~part3 #2~

右の図のように、
直線①:y=x/2
双曲線②:xy=6 (x>0)
2点 A(-4,3) B(-1,-1)
がある。
また、四角形ABCDが平行四辺形となるように、2点 C , D をそれぞれ①、②の上にとる。次の問いに答えなさい。
(1) 2点 C , D の座標をそれぞれ求めなさい。
(2) 点P (3,-1) を通る直線n で、平行四辺形ABCDの面積を2等分したい。
直線n の式を求めよ。
--------------------------------------------------
この問題の (1) ですね。
前回は、点C / 点D それぞれの x座標と y座標、それら4つの値を文字2つで表して連立方程式で解く、という考え方でした。
点C の座標を (X,Y) とし 点D の座標を X と Y を使って表わしましたね。
今回は、点C の座標を文字1つだけで表わす考え方です。
それほど難しいことではないです。点C は 直線① 上にあるのだから、例えば 点C の x座標が分かるのであれば 直線① の式に代入することで y の値を求めることが出来ますよね。
つまり、点C の x座標 = t とした場合、直線① の式 y=x/2 に代入して y=t/2、y座標 = t/2 と表わせます。
あとは前回同様、点C の座標 (t,t/2) から 点D の座標を書くと、

このように表わすことが出来るので、あとは 点D の座標を 双曲線② の式に代入し t の値を求めれば良いですね。
ちなみに前回と今回の解き方、何が違うかと言うと「代入のタイミング」だけなんですよね。
分かるでしょうか?
【前回】※扱う文字は X,Y から t,u に変更してます。
C (t,u) とする。
D (t-3,u+4) となる。
C/D の値を式に代入。直線①:u=t/2、双曲線②:(t-3)(u+4)=6
直線① と 双曲線② の式を連立方程式(代入法)で解く。(t-3)(t/2+4)=6
【今回】
C の x座標 t とする。
直線① に代入し y座標を作る。y=t/2
D (t-3,t/2+4) となる。
双曲線② に代入し方程式を解く。(t-3)(t/2+4)=6
という感じで、結局どちらも同じ式(二次方程式)を解くことになります。
さて、今回の解説もきちんと伝わったでしょうか?
次回は (2) の問題の解説を書いていきたいと思います(^^)
2019年
10月
24日
木
文章問題の考え方講座 ~part3 #1~
part3は二次方程式の単元の中で出題されてた問題です。
けれど、連立方程式、比例反比例、一次関数、図形(平行四辺形)の性質、など複合的な知識の土台が無ければ解けないかな、という感じの問題ですね。
--------------------------------------------------

右の図のように、
直線①:y=x/2
双曲線②:xy=6 (x>0)
2点 A(-4,3) B(-1,-1)
がある。
また、四角形ABCDが平行四辺形となるように、2点 C , D をそれぞれ①、②の上にとる。次の問いに答えなさい。
(1) 2点 C , D の座標をそれぞれ求めなさい。
(2) 点P (3,-1) を通る直線n で、平行四辺形ABCDの面積を2等分したい。
直線n の式を求めよ。
--------------------------------------------------
今回はこの問題の (1) を解説していきたいと思います。
まずは、四角形ABCD が平行四辺形であるということ。そのことから 点C と 点D の位置関係をどのように捉えるか、が大切なポイントになります。

四角形ABCD が平行四辺形だということは、
線分AB と 線分DC は「傾き」も「長さ」も等しい
ということになりますね。つまり、
「点C から 点D の位置関係」は「点B から 点A の位置関係」と等しい
と考えることが出来ます。

点A と 点B の座標は分かっているので、点A は 点B から見て、
「x軸マイナス方向に3 , y軸プラス方向に4 移動した位置」
にあることが読み取れます。つまり、

点C と 点D の位置関係もそれと同様なので、点D は 点C から
「x軸マイナス方向に3 , y軸プラス方向に4 移動した位置」
にあるということになります。
この位置関係の情報を利用すると、点C および 点D の座標を文字を使った式で表すことができます。

点C を (X,Y) とした場合であれば、点D は (X-3,Y+4) というようにそれぞれの座標を「文字2つ」で表わすことが出来ます。
もし 点D を (X,Y) とするのであれば、点C は (X+3,Y-4) となりますね。まぁそれは、どちらの点を基準にするか、というだけのことなのでどちらでもOKです。
あとは、直線① の式に 点C の座標を、双曲線②の式に点Dの座標を、それぞれ代入して解いていけばいいだけです。
この手の問題の考え方のポイントは、
点C の x座標 (?1)、点C の y座標 (?2)、点D の x座標 (?3)、点D の y座標 (?4)
と、不明な値が4つあるわけですが、
?1 → 文字1、?2 → 文字2、?3 → 文字3、?4 → 文字4
このように、それぞれに文字を割り当てるのではなく、
?1 → 文字1、?2 → 文字2、?3 → 文字1を使って表わす、?4 → 文字2を使って表わす
こうして扱う文字の数を2つにするということ。
扱う文字が2つであれば連立方程式で解くことが出来ます。
ちなみに、扱う文字が1つであれば方程式で解くことが出来ます。ということで、次回は少し違った考え方で解く方法を解説してみたいと思います(^^)
2019年
10月
18日
金
中間テストが終わって、嬉しかったこと
この仕事をしていて一番うれしいことは、なんと言っても「子どもたちの成長を実感したとき」ですね!
成長を実感することは日々の指導の中でも多々ありますが、やはり定期テストの結果が出たときがもっとも分かりやすく、これまでの努力の成果が実感できる瞬間ではないでしょうか。
今、中学3年の女の子が二人いるのですが、私の塾に通い始めた当初はとにかく数学が苦手でどうしていいか分からない、というような状態だったのですが、
そんな子たちが前回と今回のテストで当たり前のように80点以上取れるようになってくれて、そのことがすごく嬉しくて!
なので、他にも頑張っている子はいますが、全員!というわけにはいかないのでとりあえず二人だけ、ウチの生徒たちの頑張りを自慢したいと思います(^^)

この子は1年の3学期、学年末テストの前から通塾してくれています。
入塾してすぐの学年末テストでは結果は出せませんでしたが、すぐに結果を出そうと焦るのではなく、数学の基礎部分で分からないことを棚卸しして潰していき、数学的な考え方をしっかりと身につけさせることに注力し、土台をしっかり固めていきました。
その土台が完成してしまえば成績はどんどん伸びます!というのを2年2学期の中間テスト以降に見事に体現してくれましたね。
80点以上を当たり前のように取れるようになり、自己最高記録も更新し続け、
今回は自己ベストの86点でした!
ちなみに2年3学期は体調不良で休塾しており学年末テストの記録は無し。3年1学期の中間テストは実力テストに置き換わったため記録はありません。
そして、もちろん頑張っているのは数学だけではありません!

各教科および5教科合計の、「入塾前の最低点」と「入塾後の最高点」の比較をしてみました!
国語は大きく伸びてはいないものの入塾後はコンスタントに70以上取れています。
社会/理科/英語は調子が良ければ80取れるけど60~70点台の時もあり、伸びてはいるけど安定してないので、そこを安定させるのが今の課題ですね。
ただ、体調不良も引きずっている状態なので、そのことを踏まえると本当によく頑張ってくれています!

この子は今年の始めに入塾したので、Aさんと同じく2年3学期の学年末では結果は出せていません。塾に来る前の期末の成績が良かったのでグラフにしてみると大きく下がった格好になりましたが、2学期の期末が難易度低めだった、というのが真相のようですね。
2学期 期末 :平均66
3学期 学年末:平均47
なのでこの子の学力自体は、実は大きく変わっていません。
そしてこの子も入塾してからは数学の基礎固めをしていって、3年になってからは右肩上がりに伸びましたね。自己最高記録も更新し続け、
今回は自己ベストの83点でした!

こちらも、各教科および5教科合計の、「入塾前の最低点」と「入塾後の最高点」の比較をしてみました!
入塾してから短い期間で、特に数学は大きな飛躍を遂げましたね。入塾前のこの子が今の自分を見たら本当にびっくりすると思います!数学、本当に苦手な子だったので。
国語/理科/英語はもともと50点台で踏みとどまっていたので伸びとしては大きくないかもしれませんが徐々に80点も超えるようになってきました。社会が私の想定より伸びていないので、そこが今の課題です。
こうやって成績の推移を抽出し視覚化すると、より一層その子の努力や成長が実感できてうれしくなりますね!
今回は特に頑張った二人の成長をご紹介しましたが、私の塾に通ってくれている生徒たちは、全員が自慢の生徒たちです(^^)
2019年
10月
15日
火
文章問題の考え方講座 ~part2~
ようやくpart2です。今回の問題はこちら。
--------------------------------------------------
電車が分速640mで等しい間隔をおいて走っている。A君が線路に沿って歩いたとき、前から来る電車には7分ごとにすれ違い、後ろから来る電車には9分ごとに追いこされた。A君の歩いた速さを求めなさい。
--------------------------------------------------
この問題を解くための一番シンプルな考え方は、
①:「A君」の歩く速さを a(m/分)とする。
②:「電車」と「A君」がすれ違う瞬間から7分後の、「電車」と「A君」との間の距離を文字式で表す。
③:「電車」が「A君」を追いこす瞬間から9分後の、「電車」と「A君」との間の距離を文字式で表す。
④:②と③の文字式をイコールで結び方程式を解く。
このような感じでしょうか。
実はこれだけだと不十分でこの問題の要点を正しく理解することは出来ないのですが、ひとまず「A君」と「電車」との関係を図に書いてまとめてみます。

②電車の速さは640m/分なので電車の走った距離は、640×7=4480(m)。A君の歩いた距離は、a×7=7a(m)。これらを足したものがすれ違う場合の「電車」と「A君」との間の距離です。
4480+7a
③電車の走った距離は、640×9=5760(m)。A君の歩いた距離は、a×9=9a(m)。これらの差が追いこす場合の「電車」と「A君」との間の距離です。
5760-9a
ということで、あとはこの二つの文字式をイコールで結んで計算すればいいわけですが、質問をくれた生徒が分からなかったことは、
「どうしてこの二つの式が等しくなるのか?」
ということでした。
二つの式が等しい、とする根拠は問題に書いてある通り、電車は「等しい間隔をおいて走っている」からです。
ではなぜ「電車とA君との間の距離」とそのことが結びつかないかというと、式を作るときに最初の電車とA君との関係しか見ていないから。
なぜ7分後、9分後の距離を考えるのか。
A君が最初の電車とすれ違う瞬間から7分経った瞬間がどういう状況になっているのか、追いこす場合も同じです。9分後にどういう状況になっているのか。そこが正しくイメージできていないから二つの式が等しくなる理由が分からないのだと思います。
ということで、この問題を解くための考え方を改めて図にまとめます。

問題文「前から来る電車には7分ごとにすれ違い」は、
A君が最初の電車とすれ違う瞬間から7分後 → 次の電車とすれ違う瞬間
問題文「後ろから来る電車には9分ごとに追いこされた」は、
A君を最初の電車が追いこす瞬間から9分後 → 次の電車が追いこす瞬間
だということを正しく理解しイメージできないと「式の作り方は知ってる」けど「なぜ等しい関係になるのか分からない」ということになるのですね。
もちろんこの問題を解くだけであれば「なぜ電車とA君との間の距離が等しくなるのか?」について分からないままでも支障はないです。
ただそれは「この問題を解くためだけの知識」でしかなく応用は効きません。
だから当塾では「解き方」ではなく「なぜその解き方なのか」ということを、正しく理解できるよう指導することに力を入れているのです(^^)
2019年
10月
14日
月
文章問題の考え方講座 ~part1 #4~
今回もこれまで(文章問題の考え方講座 ~part1 #1~ / ~part1 #2~ / ~part1 #3~)と同じ問題を題材に、また少し違った解き方について考えていきたいと思います。
この問題の解き方を考えるのはこれで最後です。次回からは別の問題を考えていきますね。
--------------------------------------------------
ある中学校の昨年の生徒数は、男女あわせて530人であった。今年は、昨年と比べると、男子は5%減り、女子は8%増え、合計では6人増えている。今年の男子と女子の生徒数を、それぞれ求めよ。
--------------------------------------------------
さて、この問題は連立方程式の問題ということで2年生のワークに収録されている問題なのですが、文章問題が苦手な子には「決められた解き方通りに解く」のではなく、とにかくいろいろ考えてもらいたいので、
「使う文字をxとyの2つではなく、xだけを使って解いてみて!」
と、文章問題が苦手な子には少々しんどいと感じるであろう無茶振りをしたりします。
考え方は特に難しいことはないです。
去年の男子をx人、去年の女子をy人、とすると、

このように考えたわけですが、この内「y」が使えなくなったので、「去年の女子の人数」をどのように表わすか?ということを考える必要がありますね。
去年の合計が530人、去年の男子がx人。なので、
「去年の女子の人数」=「合計から男子の人数を除いた人数」
と、これだけ考えることが出来ればいいわけです。

あとは出来上がった方程式を解けばいいだけですね。
さて、「文章問題の考え方講座」と題して一つの問題の考え方を4回にわたって書いてきましたが、こんな風に色々な解き方を考えさせることで、文章問題は苦手な子どもたちでも段々と「自分で解き方を考える力」が身についていきます。
「問題の解き方を覚える学習」はどれだけやっても社会に出たとき役には立ちませんし、なにより面白くないと私は思います。
ぜひ色々な解き方、考え方を模索して楽しんでみて下さい(^^)
2019年
9月
11日
水
文章問題の考え方講座 ~part1 #3~
今回もこれまで(文章問題の考え方講座 ~part1 #1~ / ~part1
#2~)と同じ問題を題材に、また少し違った解き方について考えていきたいと思います。
--------------------------------------------------
ある中学校の昨年の生徒数は、男女あわせて530人であった。今年は、昨年と比べると、男子は5%減り、女子は8%増え、合計では6人増えている。今年の男子と女子の生徒数を、それぞれ求めよ。
--------------------------------------------------
この問題、こんな式を書いて間違う子もいます。
昨年の生徒数、男子をx人、女子をy人とし
x+y=530
0.95x+1.08y=6
なぜこうなったのかは分かりませんが、おそらく解き方は知っていてその解き方に当てはめる値を深く考えずに問題の中から拾っていった結果、
今年の男子と女子の生徒数の合計、の式が「0.95x+1.08y=6」となってしまったのかもしれませんね。
問題の中にある「6」という値は、昨年と比較し今年の全体の生徒数が6人増えた、ということなので、今年の生徒数「男子(0.95x)」「女子(1.08y)」の合計とするなら、昨年の合計530人に増えた6人を足して536人にしなければ等式は成立しませんね。
こういう間違いも子どもたちの学びにおける大切な素材です。上記に書いた通り、
「二つ目の式の左辺を “0.95x+1.08y” とするなら右辺はどのような数を置くべきか?」
については当然指導し学んでもらいますが、当塾ではそこから先に一歩踏み込んで、
「二つ目の式の右辺が “6” になるような左辺の式を考えてみよう!」
という問いかけをして、子どもたちに解き方を考えるよう促します。
この場合、「6」という値が何を表わしているかを読み解く必要があります。
昨年の人数と比較したときの今年の人数の変化は、
男子 → 5%減った
女子 → 8%増えた
全体 → 6人増えた
男子は減って女子は増えて、けど全体では人数が増えている、ということは「減った男子の人数」より「増えた女子の人数」の方が多いから全体で6人増えている。
つまり「増えた女子の人数」と「減った男子の人数」との差が「6人」ということ。
なので、
「増えた女子の人数」ー「減った男子の人数」= 6
で等式が成立します。
昨年の人数は男子を x人、女子を y人としていて、男子は「昨年の人数の 5%」が減った人数、女子は「昨年の人数の 8%」が増えた人数。なので、
「減った男子の人数」=0.05x
「増えた女子の人数」=0.08y
これで等式を完成させることが出来ますね!
さて、今回の考え方はいかがでしたか?
方程式の解き方って考え方次第で色んな式を書いて解くことが出来て面白いと思いませんか?
用意された解き方に囚われず自由な発想で自在に思考を広げることが出来る、子どもたちにはそういう学力を身につけていって欲しいですね(^^)
2019年
7月
25日
木
文章問題の考え方講座 ~part1 #2~
第2回は前回(文章問題の考え方講座 ~part1 #1~)と同じ問題を題材に、けれど少し違った解き方について考えていきたいと思います。
--------------------------------------------------
ある中学校の昨年の生徒数は、男女あわせて530人であった。今年は、昨年と比べると、男子は5%減り、女子は8%増え、合計では6人増えている。今年の男子と女子の生徒数を、それぞれ求めよ。
--------------------------------------------------
この問題、解き方を覚えてなぞるだけの子たちがよくやるのが、「今年の男子と女子の生徒数」を「x , y」とおいて解こうとすること、ですね。
もちろんそれでも解くことは出来ますが、何%増えた減った、という変化が昨年の人数を元にしているので、今年の人数を基準に考えようとすると少し難易度が上がります。
で、どういう式を書けばいいか分からずに困り果てている子たちが非常に多いです。
「今年の男子と女子の生徒数」を「x , y」とおいて
「昨年の男子と女子の生徒数」を「x , y」を使って表わす
となるのですが、ここで必要なのが「○%増えたり減ったりしたものを、増えたり減ったりする前に戻す」計算の考え方ですね。
要するに「税込み価格を、税抜き価格に戻す」計算、と言えば分かりやすいかな。
この考え方が分からない子はとても多くて、
例えば、
男子が5%減った → 5%増やせばいい
1.05x
女子が8%増えた → 8%減らせばいい
0.92y
というような考え方で間違った式を書く子が割と多いです。
しかし「昨年の人数を元にした5%」と「今年の人数を元にした5%」というのは、値が同じ「5%」であっても、その中身は別物です。
この問題ではあくまでも「昨年の人数」を100%として考えなければなりません。
昨年の人数を「x , y」として今年の人数を表わすと、

こうでしたね。100だったものが95に、100だったものが108に、という変化をもう少し分かりやすく書くと、

このような感じでしょうか。
100だったものを95にする(100で割って95を掛ける)
100だったものを108にする(100で割って108を掛ける)
という計算です。
今年の人数を「x , y」として昨年の人数を表わす場合は、この計算を反転させればいいですね。つまり、
95にしたものを100に戻す(95で割って100を掛ける)
108にしたものを100に戻す(108で割って100を掛ける)
という計算をしてあげると、5%減る前の人数、8%増える前の人数、をそれぞれ求めることが出来ます。

これで式が二つ完成したので、あとは連立方程式の計算で解けばいいですね。
今回は求める数である「今年の男子と女子の生徒数」を「x , y」とおいて式を立てているので、計算して求めた「x , y」の値がそのまま答えとなります。
今回の考え方はいかがでしたか?
昨年の生徒数を「x , y」とおくか、今年の生徒数を「x , y」とおくか、たったそれだけの違いですが、式を書くための考え方の難易度はかなり差があるかもしれませんね。
とはいえ、今年の生徒数を「x , y」とおいて式を考えたからこそ、「方程式の文章問題の解き方」ということだけでなく「○%増えたり減ったりした物の数を、○%増えたり減ったりする前の数に戻す、割合の計算の考え方」まで学ぶことが出来るのです。
スタンダードな問題の解き方だけを教える、というのは最短ルートで効率よく思えるかもしれませんが、今回のような考え方を学んで行くことは、たとえ時間がかかって非効率的に思えても、子どもたちの地頭力を育てるとても大切な過程だと考えています。
たくさん寄り道をして、たくさん考えた子ほど、応用力が身に付きます!
ですので当塾ではひとつの考え方だけに囚われず、自由な発想でさまざまな考え方を身につけられるよう、分からない事に対し試行錯誤を重ねていく!そういう学習を大切にしています(^^)
2019年
7月
11日
木
文章問題の考え方講座 ~part1 #1~
文章問題の考え方講座 ~part1~、ということで第1回はこちらの問題について考えてみます。
--------------------------------------------------
ある中学校の昨年の生徒数は、男女あわせて530人であった。今年は、昨年と比べると、男子は5%減り、女子は8%増え、合計では6人増えている。今年の男子と女子の生徒数を、それぞれ求めよ。
--------------------------------------------------
割合の考え方を含む文章問題です。苦手な子も多いですね。
ウチの生徒がこの問題を解くときに、ココが分からなかった、こんな間違いをしていた、っていう実例も元に問題を解くための考え方を見ていきたいと思います。
まずは、この問題を解くのに一番シンプルな考え方から。
文章問題を解くために大切なことは「登場する値とその関係を正しく把握、整理して考えること」かな。この問題であれば、
昨年の男子の生徒数(不明)
昨年の女子の生徒数(不明)
その合計が530人
今年の男子の生徒数(不明、昨年より5%減)
昨年の女子の生徒数(不明、昨年より8%増)
その合計が、昨年より6人増、なので536人
男子の生徒数+女子の生徒数=合計、で等式が書けます。
これらを表にして整理するとこんな感じでしょうか。

次にこの中の「不明な値」に対し、x や y といった記号を置いて、計算によって解を求めるための数式を作っていきます。
このとき、どの値を記号に置き換えて考えるか?、というのはとても大事なポイントで、選択次第でかなり難易度が変わってきます。
この問題では「5%減」「8%増」という値が昨年の人数を元にした変化になっているので、昨年の男女の生徒数を x , y とした方が考えやすいですね。
そこから今年の生徒数を x , y を使ってどのように表すか考えます。
「5%減」は元の人数を100とした場合に、その内の5を減らして95にするということ。
「100→100」は「×1」なので「100→95」は「×0.95」です。
「8%増」は元の人数を100とした場合に、その内の8を増やして108にするということ。
「100→108」は「×1.08」です。
まとめるとこんな感じ。

これで式が二つ書けるのであとは計算するだけですね。
ちなみに求める値が「今年の男子と女子の生徒数」なのに対し、この考え方の式では「昨年の男子と女子の生徒数」を x , y としているので、連立方程式を解いたあと x , y の値から今年の人数をそれぞれ求めないといけない点には注意が必要です。
さて、今回の解説はいかがだったでしょう?
数学の文章問題を解けない子たちは、問題を解く手順が「式を書く」→「計算」の2つだけ。で、式を書く方法は「覚えてる解き方、あるいは似た問題の解き方に数値を当てはめる」ということをしているだけで「問題を読んで式を作る」ということを実はほとんどしていません。
数学が苦手な子たちは「計算することが数学」という感じですが、私の感覚では「計算するまでが数学」です。
なので、これからも式を立てるまでの考え方を色々と解説していきたいと思います(^^)
2019年
7月
07日
日
文章問題の考え方講座 ~part0~
数学の文章問題。苦手な子が多いですね。
多くの子どもが、「解き方」に当てはめて計算し答えを出そう、としかしていないことが多いですね。だから覚えている「解き方」から少しでもズレると、途端に道に迷い、訳が分からなくなってしまうのだと思います。
文章問題を解くのに大切なことは「解き方」ではなく「考え方」です。
では、その「考え方」を養うためにはどうすればいいのでしょうか?
私はあまり小難しくは考えていません。
【寄り道をして、その問題でたくさん遊んでしまえばいい!】
そんな風に考えています。
型にはめて問題を解いて、正解すれば「ハイ終わり」ではなく、
じゃあこうしてみたらどんな式が書けるだろう?
こんな風に考えたら別の式が書けないかな?
と、想像力を膨らませ、一つの問題に ああでもない こうでもない とひたすら思考をめぐらせ自由自在に「解き方」を開発する。
そういう勉強は、未知の問題であろうと解に辿りつける実力が身につくだろうし、なによりきっと楽しい!
そこで当ブログでも「文章問題の考え方講座」シリーズとして、子どもたちが間違いやすいポイントと、それでも躓かずに前に進むための考え方を養っていけるような内容を投稿していけたらと思います。
それでは「文章問題の考え方講座 ~part1~」をお楽しみに(^^)
2018年
10月
17日
水
中間テスト、とある生徒の努力の結果
中間テストの終わりに合わせて今回作ったチラシです。↓
一番新しい生徒の成績の推移をご紹介させて頂きましたが、チラシ作成時に社会のテストが未返却のままだったため中途半端なデータの掲載となりました。
こちらの生徒の成績が出そろったので改めて努力の成果をご紹介します(^^)
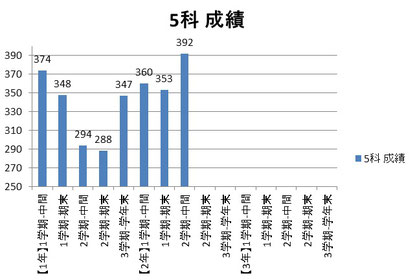
勉強という行為においてもっとも大切なことは、
「理解の追及」
である、というのが私の考えです。
中学生に対して100%完璧な理解、なんてものは求めませんが、その子なりに納得できる形の理解を得る、というところまでは絶対に妥協はしません。
問題を終わらせたいだけで理解を求めようとしない姿勢での学習は絶対にさせません。
なので子どもたちにとって私の指導はきっと厳しいものだと認識しているのですが、その厳しい指導を受けとめ、しんどいながらも一生懸命努力を続けてくれている生徒がこうして結果を出してくれるのは、本当に心の底から嬉しい気持ちになりますね!
また、本人もテストの結果に本当に嬉しそうにしていて、「次は400以上目指したい!」と学習意欲はさらに向上しています♪
勉強は嫌いかもしれない。しんどいし楽しくないかもしれない。
けれどそれでも頑張って結果が出せたときはやっぱり嬉しい!頑張ってよかった!勉強、ちょっとだけ楽しいかも!
一人でも多くの子どもたちに、こんな風に思ってもらえるように尽力して参ります(^^)
2017年
4月
03日
月
応接 兼 読書スペースをリニューアルしました
今年は、「この地域の子どもたちに読書の面白さや大切さを伝えていく」ということに力を入れていきたいと考えています。
そこで!

教室の東側、「応接スペース」として使っていたところを、「応接 兼 読書スペース」としてリニューアルしました(^^)
今年度は週末なんかに、「勉強ができる子どもに育てる」ための読書会を開催していきたいと考えています。勉強ができる子どもを、といってもやることはシンプルで、ただひたすら読書を楽しむための会、にしていけたらなと思っています。
小学校低学年くらいまでの小さい子には読み聞かせをしてもいいですね。
本棚の方はまだまだ整理しきれていませんし、これからどんどん増やしていきたいと思います。当面、増やしたいのは文庫本ですね。
小中学生くらいの子が読んで、「面白い!」って思えるような本を増やしていくつもりです。
塾に通う、だとか、塾で勉強する、ってことはとりあえず置いておいて、そんなことよりもウチの生徒や、地域の子どもたちが気軽に本を読みに来れるような場所にしたいですね(^^)
2017年
3月
29日
水
春期講習の特典が決まったようです。
今年の春期講習には特典として、
「映画鑑賞」と「小説本」のプレゼント
を付けています。
小説本をプレゼントするのは、読書をしない子どもたちに本を読む面白さを知ってほしいから。
映画もセットにしてあるのは、先に映画をみてイメージを作っておくことで、文章を読むハードルを少しでも下げてあげたいから。
そういう理由で特典を付けました。
で、春期講習に来てくれた子にリクエストを聞いていたのですが、とりあえず決まった子の分をお昼の空き時間に買ってきました。

「ひるなかの流星」と「ひるね姫」ですね。
どちらもCMなどでよく目にするので知ってはいますが、話の内容までは知らないので、小説の方は自分用もあわせて2冊ずつ買っています。
生徒が本を読み終わった時に、感想を言い合ったり、共感したりしたいですもんね。
そういうのが読書の楽しさの一つでもあると思うので。

あと、もう一冊あって。「夢の終わりで、君に会いたい。」という本ですね。
こちらは、速読で通ってくれている子が今読んでいる本、ということで、こちらも一緒に購入しました。
計3冊。今週末にでも時間作って読んでしまいたいと思います!
生徒たちのおかげで楽しみが増えました(^^)
2017年
3月
24日
金
調査書評定と公立高校入試(大阪)の内申点について
公立の中学校は今日が修了式だったので、通知表や調査書評定などをもらって帰ってきたのではないでしょうか。
ということで、その評定が公立高校入試の内申点にどうかかわってくるのかを説明します。
まず内申点について。
ご存知の方も多いと思いますが、昨年の入試までは「3年生の時の成績のみ」が内申点となっていましたが、平成29年度入試、つまり今年の入試からは内申点の算出方法が下記のように変更になっています。
平成29年度入試(今年)
2年生:3年生 = 1:3
平成30年度入試(来年)
1年生:2年生:3年生 = 1:1:3
つまり、次の4月から3年生になる子たちは、1・2年生の時の成績も内申点に含まれます。
具体的には、
「1年生の時の調査書評定 x 2」
+
「2年生の時の調査書評定 x 2」
+
「3年生の調査書評定 x 6」
の合計が高校入試の時の内申点のベースとなります。
評定は9教科5段階評価なので、最大で45。
1・2年の評定が45x2=90、3年が45x6=270、90+90+270=450点が満点として算出されます。
例えばお子様が1年生、調査書評定がオール3だったとしたら、
3x9x2=54
なので、90点満点中54点、というのが1年の内申点となるわけですね。
高校入試では、このようにして算出した内申点に各学校ごとの倍率(1.4倍、1.2倍、1.0倍、0.8倍、0.6倍)を掛け合わせた点数と、入学試験の成績(これも学校ごとに定められた倍率を掛け合わせた点数)を合計し900点満点で合否を判定していくことになります。
高校によって試験重視、内申重視と差はありますが、中学3年間の成績(テストだけではなく提出物がきちんと出せているか、授業での態度など)が、公立高校入試において大きなウエイトを占めていることが分かると思います。
中学1、2年の子どもたちからすれば高校入試なんて何の実感もないし、ピンと来るものは何もないという子がほとんどだと思います。
なので、3年になって、いざ受験!というときに後悔することの無いよう、大人たちがしっかりと受験の制度や仕組みについて伝えていってあげなければいけないですね(^^)
-----
今回の記事の情報ソースは下記より。
大阪府 公立高等学校入学者選抜
http://www.pref.osaka.lg.jp/kotogakko/gakuji-g3/
平成29年度選抜
↓
○中学1、2年生と保護者のみなさんへ
↓
入試での調査書評定の活用方法等について [PDF]
2017年
3月
22日
水
テストに対する評価の仕方
今日はテストの点数の見方について。
例えば「点数だけ見る」のと「平均点との比較で見る」のとでは、その評価が180度変わる場合もあるので、その例を紹介します。
なお、下の紹介例は実際の生徒の成績をベースにしたダミーです。
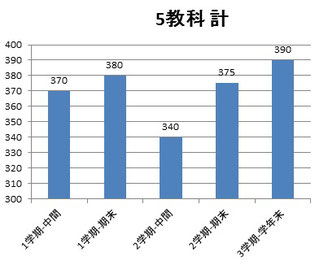
まず、5教科の合計点ですね。
点数だけだと、2学期の中間で大きく下げたように見えますね。
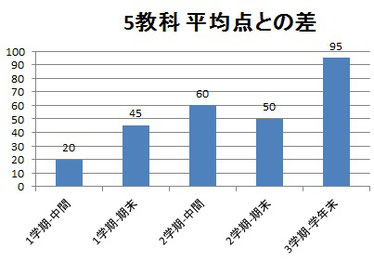
先ほどの成績を5教科の平均点と比較し、その差をグラフにしたものがこちらです。
大きく下げたと思われた2学期中間テストですが平均点との比較で見ると、実は前回よりも成績が伸びている、と評価することができます。
つまり、点数だけ見ると、1学期期末から40点下がっているが、全体の平均点の方がそれよりも多く55点も下がっているので、総合的に見れば成績が伸びているんですね。
もちろん「平均点」自体がそこまで信頼のおける指標ではないのですが、子どもの成績単体で評価するよりは、十分に子どもの努力を計ることができると思います。
「テストの成績単体ではなく平均点も考慮すること」
これが、子どもの勉強に対する評価をする指標として成績を見るときの大切なポイントですね。
あと、もう一つ。最も大切なポイントは、
「数字そのものではなく、そこから見える子どもの努力を評価すること」
だと、僕は考えています。
上の例なら、「全体が55点も下げてる中、40点ダウンで踏みとどまった」のは紛れもなくその子の努力の証です。
また、ココではあくまで成績から努力を読み取るときの話をしていますが、自分の努力がなかなか成績に反映されない子もたくさんいます。
もちろん成績から読み取れないだけで、その子なりに一生懸命努力している部分は少なからずあるはずです。
そういう場合は成績という数字ではなく、中身であったり、普段の勉強の様子、テスト前の勉強の様子から、その子の頑張りをちゃんと見つけて認めてあげることで、次へのやる気に繋げていくことが大切です。
テストの点数に対して怒ったり、否定するようなことをするとほとんどの場合、子どもの成績が伸びることは無い気がします。
もちろん、それをバネに頑張れる子もいるでしょうけど。
けれど、そういう子どもも含め、基本的に子どもというのは「親に認められたい」という欲求が強く、それが満たされることがなにより嬉しいし、また力へと変わります。
はい。
書いているうちに、あれもこれも言いたくなって、少しまとまりがなくなったかもしれませんが、お子さまの成績を伸ばしてあげたいのなら、ここで読んでいただいたことを参考に子どもへの声掛けを内容を変えてみて頂ければ幸いです(^^)
2017年
3月
21日
火
高校入試の結果(2017)
そういえばブログの方で書いていなかったので、今年の高校入試の実績報告です。
はい!
今年も当塾の受験生は全員合格しました!去年に引き続き、合格率100%です!!
[私立]
大阪学院大学高等学校(特進):1名
[公立]
吹田高校:1名
Congratulations!!
今年は受験生が一人という少しさみしい環境でしたが、コンスタントに努力を重ねてくれました。自分で選択し、自分の努力で勝ち取った進路を、4月から力いっぱい進んでいって欲しいと思います(^^)
さて、もうお気づきだと思いますが、今年の受験生は一人だけだったんですよね(^^;
母数が「1」の合格率100%!、これほどあてにならない100%もあまり無いような気がしますが、それでも合格は合格。
「ウチで勉強した生徒は、絶対に志望校に合格させます!」
受験者数が1人だろうが、10人だろうが。来年も再来年も。
今後もずっとこういうことを胸を張って言えるように、私自身が指導者としてもっともっと成長していきたいですね。
生徒たちが、
「この先生が言うんだったら、頑張ってみようかな」
って、そんな風に思ってもらえるような先生に、これからもっともっとそうなっていけるように努力していきます(^^)
2017年
3月
17日
金
春期講習、よくある質問
一昨日、春期講習のチラシを配ったのですが、さっそく数件のお問い合わせを頂きました。地道にポスティングで配っているのですが、割と反応良いですね。
新聞折込、無料新聞やフリーペーパーへの広告掲載など色々と宣伝を打ったりしてきましたが、実はポスティングが一番反応良かったりします(^^;
さて、その春期講習ですが、よくいただく質問があったのでブログでも答えておこうと思います。

Q:7日間の日程のうち何日かは予定があって行けないのですが大丈夫でしょうか?
A:はい。大丈夫です。一応この7日間を春期講習の枠として取っていますが、多少この枠をはみ出しても大丈夫です。期間内に来れない分は、3/27より前に何日か取ってもらってもいいですし、4/4以降に来てもらっても構いません。
Q:1日の授業時間はどのように設定されていますか?
A:生徒ごとに個別で指導と学習を進めていくので、学習スピードの違いによって増減がありますが、基本2時間の学習をベースに区切りのよいところまで、あるいは生徒のやる気や集中力が保てる範囲で頑張ってもらいます。
当塾の春期講習のゴールは、
「決められた回数だけ通塾して、決められた時間だけ勉強する」
ということではなくて、
「苦手だった単元がちゃんと分かるようになった!」
「次の学年で習う範囲の問題がばっちり解けるようになった!」
といった成果をしっかりと手に入れてもらうこと。
なので、期間や時間の枠から多少はみだすことは特に問題では無い、と考えています。
ですので通塾日や学習時間などで色々と制約がある場合でも、まずはお気軽にご相談いただければ幸いです(^^)
2017年
3月
16日
木
2016年度の実績
当塾でも春期講習生の募集など行っておりますが、この時期は新年度に向けた塾探しをしている親御さんも多いと思います。
塾を選ぶ際の基準はそれぞれあると思いますが、その中でも最低限の基準が、
「しっかりと成績が伸びること」
ではないでしょうか。
当塾では「成績よりも学力を伸ばす」ことを大切に考えています。ちゃんと学力を伸ばしてあげれば成績の方は自然と伸びるからです。
ですので教育の観点から言えば成績のみに固執することはしていません。ただ、生徒の勉強へのモチベーションを高める、ということにおいては別で、
「生徒に努力をさせた分だけ、絶対に成績は伸ばしてやろう!」
という想いで指導に当たっていますので、そういう意味で成績を伸ばすことは子どもの学力を伸ばすうえで非常に重要な要素であると考えています。
ということで、当塾の2016年度の生徒たちの成績がどの程度伸びたのか、ご紹介したいと思います。
なお、ご紹介する成績は「5教科の合計」ではなく、「5教科の合計と学年の平均点と差」を出しています。
例えばグラフの中で「136点」ということなら、「学年平均+136点」というのがその子の成績ということです
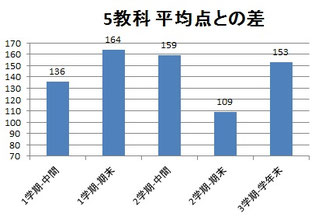
中1:Aさん
この子は小4の頃から週1で通っていたのですが、2学期になって成績が落ち込み、その後、通塾を週3に切り替え本格的に塾の方で学習を進め見事にV字回復を遂げてくれました(^^)
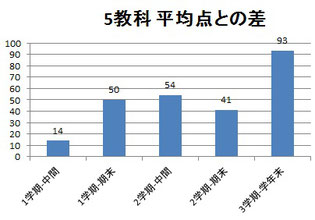
中1:Bくん
この子は小6の頃から週2で通っている子です。ケアレスミスが多いのと中学のテストに戸惑って少し伸び悩みましたが1年の終わりで実力を発揮してくれましたね(^^)
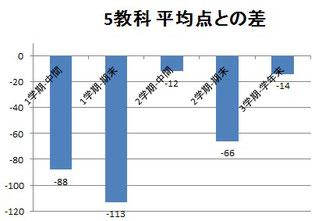
中1:Cくん
この子は中1の2学期からうちに来てくれた子です。2学期の期末は準備が足りず少し落としたものの、当塾に来る以前と比べると成績の差は一目瞭然。次は平均点を超えるのが目標ですね(^^)
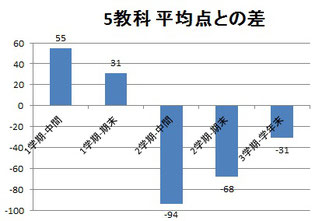
中1:Dくん
この子は2学期の中間で大きく成績を落として、そこからウチで勉強するようになって徐々に復活を遂げている最中です。この子も次の目標は平均点越えです(^^)
ということで、実績の全てということではないのですがいくつかご紹介させていただきました。
伸び幅の大小は様々ですが生徒の成績の方は全員、確実に伸ばすことが出来ています。
4月からの新年度に入って「絶対に成績を伸ばしてあげたい!」とお考えであればぜひ一度、当塾までご相談ください(^^)
2017年
3月
15日
水
春期講習の特典について
今年もギリギリになってしまいましたが、確定申告の書類も無事提出させていただきました。
この時期は学年末テストや高校入試のタイミングと重なるのでついつい後回しにしてしまうのですが、これで一安心といった感じです。
さて、今日は今年の春期講習の特典について書こうと思います。

チラシのこの部分ですね。
勉強ができない、勉強が苦手、そんな生徒たちを見ててつくづく思うのは、
「読書の習慣さえ身につけていれば、勉強がずっと楽になるのに」
ということ。
「本を読むことが大好きになって たくさん本を読むようになれば それだけで成績は上がっていく」というのが僕の持論です。
教科書や参考書、問題集、など勉強に必要なものは全て文字・文章で構成されているのだから読書力の有無で成績に差が出るのは必然ですよね。
読書と勉強の関係については、また別の機会に詳しく書きますが、とにかく子どもたちにはたくさん本を読んでほしいと思っています。
ということで今年の春期講習にこのような特典を付けさせていただきました。
で、小説本のプレゼントは前述の理屈から分かるけど、「何で映画も?」と思われるかもしれないので、その点についても答えておきたいと思います。
本を読んでほしい、けど、そもそも本を読む習慣がない子に本を読めと言ってもなかなか読むようにはならないですよね。
その要因の一つとして、「文章を読んでも表情や情景がイメージできない、だから読んでみても面白くないし、読みたいと思えない」ということがあるのかな、と思っています。
文章からイメージが作れないなら、先にイメージを用意しておけばいいんじゃないか、というのが特典に映画鑑賞をつけている理由です。
「文章からイメージを創る」より「文章とイメージを繋げる」だけの方がずっと難易度は下がるので、読書の面白さを感じやすくなると思っています。
ちなみに観たい映画は「小説本があるものなら何でもOK」です。
子どもにはなるべく楽しく勉強ができるようになって欲しい、という考えをお持ちでしたら、ぜひ一度ご相談に来てみてください(^^)
2017年
3月
14日
火
春期講習チラシのキャッチコピーについて
年が明けてから、3年生の高校入試、1・2年生はチャレンジテスト&実力テスト&学年末テストとテストラッシュでしたが、3年生の公立入試も終わりようやく落ち着いてきました。
とは言え、確定申告や春期講習と新年度に向けた準備など、やることは盛りだくさんなので、ますます頑張っていきたいと思います!
ということで、今回は春期講習のチラシに書いたキャッチについてです。

はい、こちら↑のチラシですね。
「正解」ではなく「理解」にこだわる学習指導だから、
成績アップだけでなく、「学び、考える力」が育ちます!
というキャッチコピーを書かせていただいています。
どういうことか?
まず「問題を解く」のは何のためにやっているのか?
「正解」することが目的ではありません。
教わったことをきちんと「理解」出来ているか、その確認のためです。
もちろん正しく「理解」していれば「正解」を得られます。
勉強をするうえで、その目的が「正解」か「理解」か、その姿勢のあり方は非常に重要なことです。
例えば、二択の問題があったとして、「A」と書いて不正解だったとします。「正解」することが目的、という姿勢であれば、何も考えずに残りの選択肢「B」を書きさえすれば学習は終了となります。
ただ、それは「勉強」ではなく、ただの「作業」です。
そこに「学び」や「成長」はありません。
「理解」することが目的ならば、その問題について「何が間違っていたのか」「何が正しいのか」と、色々と考えたり、調べたり、先生に質問したりして正しい「理解」を得ようとします。
その過程こそが「勉強」だと僕は考えています。
「正解」ではなく「理解」
それはつまり「作業」ではなく本当の「勉強」をしてもらうために、塾を開いてからずっと一貫した、僕の「学習指導におけるこだわり」なのです。
「正解」ではなく「理解」
「作業」ではなく「勉強」
「成績」ではなく「学力」
教育において、こういった考え方に共感いただける方はぜひ一度、当塾までご連絡頂ければ嬉しく思います(^^)
2016年
12月
05日
月
つきっきりの個別指導で成績は伸びるのか?
電話でお問い合わせを頂いた時に、「個別指導の内容が1対1や1対2など、先生がずっとついていてくれるタイプなのかどうか」、ということを確認してくる親御さんが割とおられます。
要は、
「先生がつきっきりで見てくれる」 = 「手厚い指導」
という誤ったイメージが強いようです。
はっきり言います。
こんなことをしていたら子どもの学力が伸びないどころか、ますます勉強ができなくなる可能性が高いです。
理由は明確で、子どもが先生に依存しすぎるから、です。
先生が教えれば教えるほど、子どもは自分で考えることをしなくなります。分からないことを、先生に教えてもらうことが「勉強すること」だと思い込んでいる子が本当に多い。
勉強の主役となるのは先生ではなく子どもたちです。
「先生が教える時間」よりも「子どもが自分で考えて試行錯誤する時間」が長ければ長いほど子どもの学力は伸びていきます。
先生が「教える」のは情報をインプットしているだけです。学校の授業、集団塾の講義、個別での指導、映像授業、参考書など全て情報のインプットです。
勉強とは、
それらのインプットされた情報を、自分の頭の中にある知識や言葉を使って自分なりの解釈に置き換えること(理解すること)。
「理解したと思う」ことを、問題を解いて実践することで「自分の理解が間違っていない」ことを確認すること。
大切なのはこの2つです。
こういうことはスポーツに置き換えると分かりやすいと思います。
例えば、サッカーでも野球でも何でもいいですが、コーチが言葉で説明したりお手本を見せるだけで子どもの技術が上達することはないですよね。
子ども自身が実践しなければ絶対に上達しません。
勉強も同じです。
子どもに必要な情報を的確に、かつ簡潔に指導し、あとは子どもたちがたっぷり時間をかけて教わったことを実践し、間違ったり上手くいったりを繰り返すことで学力は伸びていきます。
個別指導を選ぶ時のポイントは、
・子どもが自分で考え試行錯誤できる時間がたっぷりあるかどうか
・子どもの試行錯誤をちゃんと見守り、必要に応じて的確な指導をしてくれるかどうか
だと私は考えています。
こういった考え方を塾選びの際のポイントとして、頭の隅にでも置いて頂ければ幸いです(^^)
2016年
11月
29日
火
学力を伸ばす子どもの褒め方
当塾ではテストが終わるごとに生徒の親御さんに言っていることがあって、
それは、
「テストの成績だけを見ず、お子さんの頑張りをちゃんと見て褒めてあげて下さい」
ということ。
中学生くらいだと反抗期もあって、親の言葉を素直に受け止めることが難しい時期ではあるけれど、何だかんだ言っても親に褒められたり認められることは、子どもにとってとても嬉しいことです。
テスト前、一生懸命勉強している姿を見ていればそれだけで褒めることは出来ますし、テストの答案と問題にちゃんと目を通して「お、ここは頑張ったな!」と思えるところを探してあげて欲しいと思います。
ちなみに「子どもの褒め方」について、ちょうど何週か前の「林先生が驚く初耳学!」で紹介されていましたね。
「頭がいいね」と子どもの能力を褒めた場合と、「良く頑張ったね」と子どもの努力を褒めた場合、前者の子どもたちは段々と学習への意欲が失われ成績が低下したという結果が出たそうです。
子どもには勉強を通じて、目標に向け努力することを身につけ、その大切さを実感することができる。そんな指導をぜひ心がけて欲しいと思います(^^)
----------
「林先生が驚く初耳学!」で紹介された内容は ↓ のサイトに詳しくまとめてあったので興味があればご覧ください。
2016年
11月
28日
月
たった3週間だけで定期テストの成績は上がるのか?
気が付けば7/12からブログの更新が止まったまま。。。
あまり気負わず、のんびりと更新していけたらと思います。勉強でも何でも、大切なのは「継続すること」ですからね。
さて、時期的には期末テストが終わったり、今まさに期末テストの最中だったり、というタイミングですが、今回は前回の中間テストの結果について。
とりあえず既存の塾生はほぼ現状維持。300~450位の範囲でそれぞれ目標としている結果が出せています。
なのでこの辺りのことは置いておいて、9月の終わりくらいからウチの塾に通い始めた生徒のケースをご紹介します。
<通塾前>
1学期中間:約260点、期末:約220点
<通塾後>
2学期中間:約280点
テスト前、3週間ほどの学習で約60点アップを達成してくれました。
私の実感ですが、塾に通ってちゃんと勉強をしているなら、その期間がテスト前の3週間だけであったとしても、確実に成績は上がる、ということ。
ここで言う「ちゃんと勉強をしているなら」というのは、
・分からない所を分かるまで
・覚えるべきことを覚えるまで
勉強するということ。
塾側の視点で言うなら、この2点をきっちり押さえて指導することですね。
今現在、
・お子さまの成績低下に不安を感じている
・塾に通っているのに成績が伸びない
といったお悩みをお持ちでしたら、「成績の上がる勉強のやり方だけ教えて下さい!」なんてご相談だけでも大歓迎!
ぜひお気軽に当塾までご相談ください(^^)
2016年
7月
12日
火
期末テスト結果(2016年度 1学期)
遅くなりましたが生徒たちの頑張りを発表したいと思います。
発表対象はいつも通り「70点以上」とします。
中1(3名)
国語: 83点・71点
社会: 83点・70点・70点
数学: 87点・85点
理科: 98点・85点
英語: 97点・80点・71点
中3(2名)
国語: 86点
社会: 79点・77点
数学: 88点・70点
英語: 72点
5名中2名は平均点が下がっている中での成績アップ!、残り3名は点数自体は下がっていますが平均点の下げ幅より小さい範囲で収まっている、つまり平均点を比較の基準にして考えれば中間よりも成績アップしている!ということですね。
ウチの生徒たちはいつも本当によく頑張ってくれます。頑張った分、それがちゃんと成績に反映されることを実感として知っているからだと思います。
次の定期テストは夏休みの頑張りが大きなカギ!
テストで思うように結果が出せなくて苦しんでいる子がいれば、この夏はアチーブメントで「絶対に結果につながる勉強」をしに来ませんか?
さて、今回のテストも全員良く頑張りました!
Congratulations(^^)
2016年
7月
02日
土
期末テスト結果:速報(2016年度 1学期)
期末テストも終了し、ちらほら結果が返ってきています。一部ですが生徒たちの頑張りの成果を発表していきます。
発表対象はひとまず「70点以上」とします。
中1(3名)※内2名一部未返却
国語: 71点
社会: 70点
数学: 87点
理科: 85点
英語: 97点・80点・71点
中3(2名)※内1名未返却
国語: 86点
社会: 79点
数学: 88点
英語: 72点
期末テストは、ただでさえ内容が難しくなるのに加え、学習期間が中間テストから1ヶ月しかなく授業も駆け足で進むので学年平均も中間より下がるのが普通ですが、そんな中みんな良く頑張りました。
テストが終わった瞬間に次のテストの準備をスタートさせているので、それに沿ってコンスタントに頑張ってくれた結果ですね。
期末テストの頑張りの成果については、全員の結果が出そろい、また平均点などの情報を見てから改めて評価したいと思います。
テストの点数はさておき、今回のテストもウチの生徒は一人ひとりがそれぞれ自分のできる最大限の努力をしたことは間違いありません。
テスト勉強、本当によく頑張りました!
Congratulations(^^)
2016年
7月
02日
土
冠詞や単数複数の扱いについて
期末テストの英語で97点だった生徒の解答でこんな間違いがありました。
問題:次の日本語に合うように( )に適切な英単語を入れましょう。
あれはあなたの犬ですか。
Is that ( ) ( ) ?
この問いに ( your ) ( dogs ) と回答していたので、「何で複数形にしちゃったの?」と聞くと、「上の方の問題で I don't like dogs. という英文があって、それで dogs なのかなって思った」んだそうです。
ということで、この二つの文における dog の違いについて書いてみたいと思います。
まず、
あれはあなたの犬ですか。
Is that ( ) ( ) ?
この問題の答えは your dog ですね。主語が that で単数なので that が指す名詞 dog で単数になります。be動詞の文はbe動詞を挟んだ主語と名詞がイコールの関係になるんですよね。
次に、
I don't like dogs.
こちらは「私は犬が好きではありません」という意味の文ですね。犬が好きか嫌いか、という話題は普通はある一匹の犬を指して言っているのではなく、犬という生き物全般が好きか嫌いか、という話ですよね。なので dogs というように複数形で表現するんですね。
さて、ところで英語というのは名詞に a や the などの冠詞を付けるか付けないか、複数形にするかしないか、で大きくニュアンスが変わるのですが、中学生にはその区別が難しくてよく分からない子も多いと思います。
ですので少し例を挙げてみたいと思います。
I like dogs.「私は犬が好きです」
→犬という生き物全般が好きというときに使う言い方ですね。
I like a dog.「私は(ある一匹の)犬が好きです」
→犬という生き物全般が好き、というニュアンスは無くなって「この犬だけが好き」という感じ。
I like the dog.「私はその犬が好きです」
→この前にある特定の犬の話をしている流れで、その特定の犬を指して好き、という感じですね。
I like dog.「私は犬の肉が好きです」
→この文の dog のように、単数形の名詞の前に a や the の冠詞など何の限定詞もないと、それは必然的に「数えられないもの」を表すことになり、数えられない dog と言えば素材として意識されて「犬の肉」というニュアンスになるようです。なので「犬が好き」と言いたくて I like dog.
などと言ってしまうとネイティブの人は「犬の肉を食べるのか」と思ってかなりいやな顔をするかもしれません(^^;
パッと見、どれも同じように「犬が好き」と言っているように見えて、伝わる内容がかなり違ってくるのですね。
こうして冠詞の有無、複数形にするしない、でどんな変化があるのか、それが分かれば何となく冠詞や単数複数の扱い方も見えてくるのではないでしょうか(^^)
2016年
6月
02日
木
中間テスト結果(2016年度 1学期)
先週末で中間テストは全て終了し、テストの結果も全員出揃いましたので生徒たちの頑張りの成果を発表しておきます。
内容はシンプルに「70点以上」の結果のみとします。
中1(3名)
国語: 89点・70点
社会: 100点・82点
数学: 98点・83点・76点
理科: 96点・84点・79点
英語: 100点・98点・73点
中3(2名)
社会: 70点
数学: 84点・79点
1学期の中間テストは比較的簡単なのでしっかりと点数を取らせてあげられます。
特に1年生は中学最初のテストということで平均点が70前後になるくらい易しいので、しっかり準備を整えてあげることで良いスタートを切らせてあげることが出来ますね!
みんな、本当によく頑張りました!
Congratulations(^^)
2016年
3月
18日
金
公立入試の結果
今日は公立高校の合格発表の日。
ウチの生徒は全員(といっても今年は2人だけですが)公立が本命だったので、朝から気合を入れて待っていました。
10時を過ぎて直ぐに連絡があり、結果は、
全員合格!!
2人とも見事に自分が希望した進路を自分の力で勝ち取ってくれました!
2016年度の公立入試の結果です。
大阪市立汎愛高校(普通):1名
大阪市立西高校(情報科学):1名
毎日遅くまで受験勉強を頑張って、努力を重ねてきた結果です。
自分の力でつかみ取ったこの道を胸を張って歩いていってほしいと思います!
本当によく頑張りました!
二人とも、合格おめでとう!!!!
2016年
3月
01日
火
高校入試の英語長文読解のコツ ~実践編~
前回の続き。
実際に大阪公立入試2015年度後期A選択の問題を、
「読みながら解く」
「意味のカタマリごとに区切って前から順に読む」
の2つのポイントを押さえながら解いていってみたいと思います。
あとは、なるべく「中学生くらいの英語力だったら」ということも意識して書いてみますね。
--------------------------------------------------
では、□1 [II] の問題をやってみましょう。
まずは問題をひと通り確認します。
(1)~(4)は本文中に設問箇所がある問題、(5)~(6)は本文全体の内容を把握していないと難しそうです。
ということで、本文を見ていきましょう。
What is / your favorite Japanese coin?
何ですか / あなたのお気に入りの日本の硬貨
Jane's favorite coin / is the five yen coin.
ジェーンのお気に入りの硬貨は / 5円玉です
After her speech, / I [ ① ] interested / in
coins.
彼女のスピーチの後 / 私は興味を [ ① ] / 硬貨に
問(1)
「~に興味を持つ」は「become interested in ~」なので答えは「イ」の「became」ですね。熟語が分からなくても他の選択肢を見れば「asked 尋ねた」「found 見つけた」「took 取った」は当てはまらないので消去法で考えても答えは見つかりますね。
So, / I began / to learn / about
them.
そんなわけで / 私は始めた / 学ぶことを /
それらについて
In Japan, / six kinds of coins / are usually used.
日本では / 6種類の硬貨が / 通常使われている
Among (A) them, / the five yen coin / has a hole.
それらの中で / 5円玉は / 穴があいている
問(2)
「それら」が指しているものを直前の文から探せばいいですね。問題には「ひとつづきの英語4語」というヒントまで書いてくれているので、答えは直前の文の主語である「six kinds of coins」を抜き出せばOKです。
The fifty yen coin / has a hole, / too.
50円玉 / 穴があいている / ~も
[ ② ]
I think / there are some reasons / for that.
私は思う / いくつか理由がある / そのことには
問(3)
選択肢の英文が何を聞いているかを見ていくと、
ア:When did they begin to have holes? → いつ?
イ:How do people make holes in them? → どのように?
ウ:Who told people about holes? → 誰が?
エ:Why do they have holes? → なぜ?
とそれぞれ聞いていて、設問部の次の文で「理由がある」と言っているのだから「なぜか?」を訊ねる文が適切そうです。なので答えは「エ」の「それらにはなぜ穴があいているのか?」ですね。
For example, / if some coins have holes, / we can easily / tell coins with holes from coins without holes.
例えば / もしいくつかの硬貨に穴があれば / 私たちは出来る簡単に / 穴のあいた硬貨と穴のない硬貨とを区別する
※本文の後の(注)のところで「tell A from B」「AとBとを区別する」と書いてくれているので前置詞の前で区切らず tell 以降をまとめて訳します。
Coins / with holes / are used /
in some other countries, / too.
硬貨は / 穴のあいた / 使われている /
いくつかのほかの国々で / ~も
The designs / on coins / are very interesting.
デザインは / 硬貨の / とても興味深い
Do you know / that animals are often used / as the designs / on coins / in other countries?
あなたは知っていますか / 動物がしばしば使われた / デザインに / 硬貨の / 他の国々で
Jane gave me a coin.
ジェーンはくれた 私に 硬貨を
She brought it / from Canada.
彼女は持って来た それを / カナダから
A polar bear is used / as the designs / on it.
ホッキョクグマが使われていた / デザインに / それの
Also, / look / at this picture.
それに / 見て / この絵を
A tiger is / on a coin used / in India.
虎です / 硬貨に使われた / インドで
People are often used / as the design / on coins / in the world, / too.
人々はしばしば使われた / デザインに / 硬貨の / 世界で
/ ~も
How about Japanese coins?
どうだろう / 日本の硬貨については
Plants are often used / as the design / on Japanese coins.
植物がしばしば使われた / デザインに / 日本の硬貨の
For example, / a rice stalk is / on the five yen coin.
例えば / 稲穂は / 5円硬貨に
Cherry blossoms are / on the one hundred yen coin, / and that is my favorite
coin.
桜の花は / 100円硬貨に / そしてあれは私のお気に入りの硬貨です
And a young tree is / on the one yen coin.
そして若い木は / 1円硬貨に
That coin was first made / in 1955.
あの硬貨は初めて作られた / 1995年に
Its design has not changed / for about sixty years.
それのデザインは変更されていない / 約60年間
Plants are also / on many coins / in the world.
植物も同様です / 多くの硬貨で / 世界の
Look / at this picture.
見て / この絵を
It's a coin used / in the UK.
それは硬貨です使われた / イギリスで
You can see a flower / on it.
あなたは見ることができる花を / それの
What designs are used / on the other coins / in the world?
どんなデザインが使われているか / その他の硬化に / 世界の
I'm going to study / about (B) that.
私は勉強するつもりです / そのことについて
問(4)
これも直前の文を見て、前から順番に直訳したものを日本語らしく並べ替えればOKです。
なので答えは「世界のその他の硬貨にどんなデザインが使われているか、ということ」、こんな感じで書ければいいでしょう。
When we visit a different country, / we will see many different kins / of coins used
there.
私たちが訪れるとき 違う国を / 私たちは見るだろう 多くの違う種類の / 硬貨を 使った そこで
I may find interesting things / about different countries / by learning / about coins
/ in the world.
私は見つけるでしょう 興味深いことを / 違う国々についての / 学ぶことによって / 硬貨について / 世界の
問(5)
①What animals is used / as the design / on the coin / that Jane gave Shun?
何の動物が使われているか / デザインに / 硬貨の /
ジェーンが俊にあげた
ジェーンがくれた硬貨はカナダから持ってきたものでホッキョクグマが使われたデザインだった、と書いてありましたね。
なので答えは「It is a polar bear.」とか「A polar bear is.」とかでOKですね。
②Is the one hundred yen coin / Shun's favorite coin?
その100円硬貨は / 俊のお気に入りの硬貨ですか
桜の花が100円硬貨に使われていて、それは自分のお気に入りだ、といっているので答えは「Yes, it is.」ですね。
問(6)
選択肢を見ていきましょう。
ア:Coin with holes / are used only / in Japan.
穴のあいた硬貨は / 唯一使われている / 日本で
イ:People are not used / as the design / on coins / in the world.
人々は使われなかった / デザインとして / 硬貨の /
世界の
ウ:The one yen coin / was first made / in 1955, / and its design / was changed some years ago.
1円硬貨は / 初めて作られた / 1955年に /
そしてそれのデザインは / 数年前に変更された
エ:Shun thinks / that coins in the world / may tell him interesting things / about defferent countries.
俊は思う / 世界の硬貨が / 教えてくれるかもしれない 彼に 興味深いことを / 違う国々について
なので答えは「エ」ですね。
--------------------------------------------------
以上、実際に過去問を解いてみましたがどうでしたか?
文のカタマリごとに分ける、というのは英語の文の構造を学ぶ上で良い勉強になると思います。
慣れてくれば区切り方の基本ルールに囚われず上手に区切って読めるようになると思います。たとえば主語は前置詞を含んでいても区切らず丸ごと訳した方が分かりやすいな、とか色々考えながらやってみて下さい。
過去問5年分の英文を全部読み終えるころにはかなり長文読解の実力が付いていると思いますよ(^^)
2016年
2月
29日
月
高校入試の英語長文読解のコツ
英語の長文問題が苦手な受験生の為に、問題を解くコツについてです。
1. 問題の解き進め方 <読みながら解く>
まずは問題をひと通り確認した上で本文を頭から読んでいきます。あとは、
本文の設問箇所にぶつかったら問題を解く
↓
続きの本文を読み進める
の繰り返し。本文を読み終わったら問題も全部解けている、という感じです。
「先に本文を全部読む」や「設問の近辺だけを見て答えを推測する」というやり方よりもリスクの少ない良いやり方だと思います。
2. 本文の読み進め方 <意味のカタマリごとに区切って前から順に読む>
次に本文の読み方ですが、「意味のカタマリごとにスラッシュ( / )で区切って前から順番に読んでいく」やり方がおすすめ。
英語は基本的に、「誰が/何が(主語)」「どうした(述語)」があって、そのあとに「誰に/どこで/いつ」などが続くだけなので、このやり方でだいたい意味は取れると思います。
問題は「意味のカタマリごとに区切る」と言うけど、どこで区切ればいいの?、ということだと思いますが、基本的には、
①前置詞(in, on, of, for, with, to, by, …)の前で区切る
②接続詞(when, that, but, because, …)の前で区切る
③「, (カンマ)」の後で区切る
④主語が長い場合は主語の後で区切る
この4つくらいを頭に入れておけば大丈夫だと思います。
他にも色々と大事なことはあると思いますが、まずはこの2つだけ覚えて実践してみて下さい。
ということで次回は大阪公立入試の過去問を使って「実践編」を書いてみます(^^)
2016年
2月
29日
月
閏年
今日は4年ぶりの2月29日ですね。
閏年は4年に1回やってきますが、実は400の倍数を除く100の倍数の年には閏年がありません。
意外と知らない人は多いかもしれません。
なぜそのようなことになっているかを簡単に説明すると、
1年=365日
として暦は作られていますが、
地球が太陽の周りを1周するのにかかる日数=約365.2422日
なので、1年で約0.2422日ズレているわけですね。4年経てば約0.9688日と1日近いズレが生じるので、この誤差を補正するために4年ごとに閏年を作って366日にしているというわけです。
ただし、閏年で補正しても4年ごとに約-0.0312日のズレが残ります。400年後には約-3.12日の誤差になるので400年の間に3回「閏年じゃない年」を作るために「400の倍数を除く100の倍数の年」を閏年から外して、
2000年→閏年
2100年→閏年じゃない
2200年→閏年じゃない
2300年→閏年じゃない
2400年→閏年
というようにしているんですね。
ということで、2/29生まれの方、お誕生日おめでとうございます(^^)
2016年
2月
27日
土
Twitterの塾公式アカウントを作りました!
昨日、Twitterのアカウントを作り、今日から運用を開始しています。
Twitterでは主に近隣の中学生に向けて、勉強のやり方やコツ、勉強に対する姿勢や考え方、国数社理英のトピック、
といった勉強関連の内容はもちろん、勉強のこと以外にも、
子どもたちが生きていくうえで大切な何かだったり、子どもたちの心がほんのちょっぴり軽くなるような、明るくなるような、くだらない何かだったり、
そんな何かをゆる~く呟いていきますので、興味があればフォローしてみて下さい(^^)
2016年
2月
12日
金
私立入試の結果
今日は私立高校の合格発表がありました。
受験までにやるべきことは全てやったし、生徒たちの努力も知っています。絶対に大丈夫、と自信をもって送り出しました。
けれど結果を確認するまではやはり落ち着かないものですね。
夕方頃に全員(といっても今年の受験生は2人だけですが)の結果の確認が取れてホッとしています。
結果は、全員合格!!
合格の報告をしてくれる生徒たちの嬉しそうな声は、私にとっても最高のプレゼントです。
2016年度の私立入試の結果です。
大阪夕陽丘学園(特進 I):1名
大阪産業大学付属(進学):1名
とはいえ、ウチの生徒は全員公立が第一志望なので気を抜いてはいれません。
ひとまず私立受験を勝ち抜いたという成功体験を自信に変えて、慢心することなく公立受験に向けて努力を重ねていって欲しいと思います。
公立入試まであと約4週間!
がんばれ!受験生(^^)
2015年
10月
28日
水
入塾後の成績
定期テスト終了後は生徒の成績、頑張りの成果を当ブログでご紹介していますが、点数だけ見ても本当に成績が上がっているのかは判断が難しいと思います。
なので、今日は生徒が当塾に入塾してからの成績の変遷を紹介したいと思います。
◆生徒A
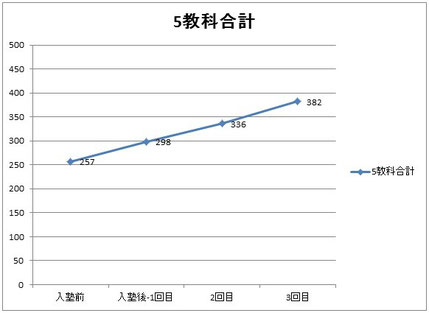
入塾前は257点まで落ち込んでいましたが、入塾後3回目の定期テストで125点アップ!
この子の次の目標は400点の壁を超えることですね!
◆生徒B
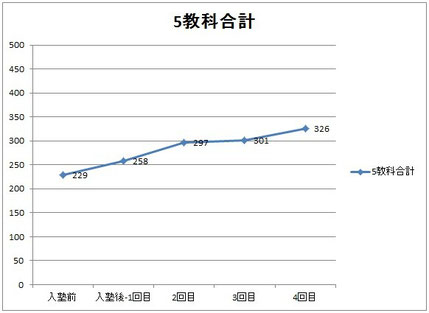
入塾前は229点まで落ち込んでいましたが、入塾後4回目の定期テストで97点アップ!
この子は英語と国語が苦手なので今後はその2教科の底上げが目標です。
◆生徒C
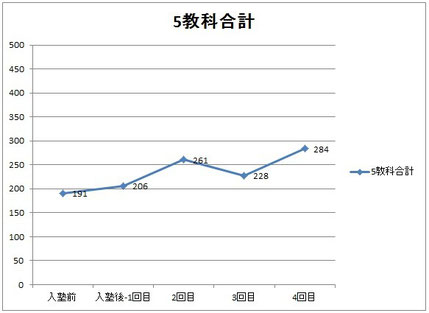
この子も入塾前は191点とかなり落ち込んでいましたが、入塾後4回目の定期テストで93点アップ!
次のテストでの目標は300点を超えることですね。
どの生徒も大体3~4回目の定期テストでプラス100点ほどの成績アップを実現できているのが分かるかと思います。
成績の悪い子どもたちは入塾した当初「自分が良い成績を取るなんて出来るわけない」と決めつけ、諦めてしまっている子が多いです。
自分は勉強しても無駄、と思ってしまっている。
だから始めは勉強することが嫌で仕方がない、ただ「やらされている」という感じにはなるのですが、それでもたくさん励ましながらとにかく勉強させることが大事です。
努力の前に結果だけを出すことは出来ません。
嫌々でもとにかく努力をさせればそれなりの結果が出てきます。
すると「頑張って勉強すれば自分だってちゃんと良い成績が取れるんだ」ということを実感として感じることができます。
そうなってくると子どもも自然に頑張って勉強するようになってくるんです。
ウチの生徒をみてても、3回目、4回目の定期テストの頃には1日5~6時間ほどの勉強でも、嫌な顔を見せたりせず進んで勉強に取り組むようになっています。
思いっきり頑張った後のテストの成績が楽しみで仕方がない、といった感じです。
これからも、もっともっとたくさんの子どもたちに「自分だってやればできるんだ!」ってことを実感させてあげたいですね(^^)
2015年
10月
27日
火
中間テスト結果、その2
先週末で中間テストは全て終了しましたね。
テストの結果も全員出揃いましたので生徒たちの頑張りの成果を発表しておきます。
内容はシンプルに「70点以上」と「10点以上UP」した結果のみとします。
中2、数学:79点
中2、理科:83点(15点UP)
中2、社会:73点(19点UP)
中2、数学:90点(13点UP)
中2、理科:88点
中2、社会:71点
中3、数学:83点
中3、国語:55点(12点UP)
中3、社会:55点(14点UP)
どの教科も入塾した当時は30~40点台でしたが皆どんどん成長してくれています!
今の生徒たちは英語が苦手な子が多いですが、もう少しで70くらいのところまでは来ているので、もうひと頑張りといった感じです。
次回のテストでは英語の成績もここで発表できるよう頑張っていきましょう!
本当によく頑張りました!
Congratulations(^^)
2015年
10月
09日
金
中間テスト結果、その1
近隣の中学校の中間テストはだいたい再来週ですね。
明日から本格的にテスト勉強を開始しますが、なかには既に中間テストがおわった子もいるので先行して成果報告しておきます。
内容はシンプルに「70点以上」と「10点以上UP」した結果のみとします。
中2、数学:79点
中2、理科:83点(15点UP)
中2、社会:73点(19点UP)
この子は英語と国語が苦手で、どちらも平均水準くらいまでは伸びてはきているものの、そこから伸び悩んでいる状況です。
ということで英国に課題はありますが、数理社はかなり伸びてきていますね。
本当によく頑張りました!
Congratulations(^^)
2015年
9月
11日
金
学力を伸ばす秘訣は、試験が終わった後にこそある
明後日、9月13日は五木模試の日ですね。
さて、その模擬試験ですが、ほとんどの子が試験を受けることだけが目的になっていて、試験が終わったらそれで終了!になっていて、テスト前は勉強しても、テスト後にしっかりと見直しをする、なんて子はほとんどいないようですね。
もちろん気持ちは分かるんですけどね。
テスト前は遊びたい気持ちを我慢して勉強を頑張っているのだろうから、テストが終わったらひとまず勉強から開放されたいというのも分かるし、一日に5教科の試験を受け終えたら体力も集中力も使い果たして疲れ切っていることだと思います。
けれど、模試を受けた後こそが自身の学力を伸ばす最良の学習タイミングです!
模試を受け終わったら解説付きの解答が配られ問題と一緒に持って帰ることができますね。
なので家に帰ったら必ず問題を解答を広げ見直しをしてください。
鉄は熱いうちに打て、の言葉通り、テストを受けたその日のうちに見直すのが最良です。
おそくとも2~3日中には必ず見直すようにしましょう。
見直しのポイントは3つです。
1. 間違えた問題、分からないところだけを見直す
見直しと言っても全ての問題を見直す必要はありません。
そもそもテストの目的は理解の棚卸しです。
基本的には、理解していることであれば問題は解けるし、理解できていなければ解けません。
なので間違えた問題だけど見直せばOKです。
ただ勘だとか、なんとなく解いたらなんとなく正解してたなど、ちゃんと理解しきれていない問題もあるとは思うので、正解していても本当に解っているか自信が無い問題も解説をしっかり読んで、「ああ、つまりこういうことか」と納得できるまで見直しましょう。
こういう問題はテストを受けた直後でないと、問題を解いたときにどう感じていたかを思い出せなくなってしまうので、テストが終わってすぐに見直す必要がありますね。
2. 見直した問題は必ず解き直す
解説を見て納得するだけで終わらない、というのも大事なポイントです。
問題の解き方を見ているのだから、その時は分かったと思えて当然です。(もちろん解説を読んでも分からない、なんてことは多々あると思いますが)
なので、見直しをして本当に理解できたのかどうかを確認する作業が「もう一度解き直す」ということになります。
テストの日は見直しだけをして、翌日に問題の解き直し、というように少し時間を置いてからチャレンジしましょう。
3. 反省点を挙げ改善策を考える
例えば数学のテストで時間が足りなかった、としましょう。
じゃあ、なぜ時間が足りなかったのかを考える。
例えば、
計算問題に手間取った
↓
何の計算に時間がかかったのか?
↓
分数の計算が苦手で時間がかかる
↓
分数の計算の演習問題をこなしてスピードアップを図る
文章問題に時間をかけすぎた
↓
残った問題は時間さえあれば解けたか?
↓
解けそうな問題だった
↓
問題を頭から順に解いていくことに囚われず、問題を見て難しいと感じたら後に回すようにする
など、上手くいかなかった原因を自問し、どうすれば次のテストで上手くいくか、自分に足りないものは何かをあぶり出し次のテストまでの勉強すべきポイントを明確にする、といったことを考え改善していくことが大切です。
ということで、せっかく模試を受けたのなら、模試の後に上記のような「もうひと頑張り」をすることで模試を120%活用し価値あるものにして欲しいと思います(^^)
2015年
8月
07日
金
肯定文での some と any の違い
前回 の続き。
今日は肯定文で使う some と any の違いについて書いていきます。
肯定文で使う any は「どんな~でも」というように後ろの名詞を強調します。
ex.) I like any Japanese movie.
私はどんな日本映画でも好きです。
some の場合は「いくつかの、多少の」という意味で、あとに続く人や物の数量を漠然と表わすときに使います。
ex.) I like some Japanese movies.
私はいくつかの日本映画が好きです。
さて、この例文、any の方は movie と単数形になっていますが、some の方は movies と複数形になっている点に注意が必要です。
some Japanese movies は「いくつかの日本映画」と言っているのだから複数形になるのは分かりますね
けど any の方は単数形になる理由は、調べてみてもいまいち納得のできる答えが見つかりません。
なので自分なりの解釈ですが、
any の方の「日本映画」は作品そのものではなく「日本映画というジャンル」を指しているから単数になる
のだと思います。
日本映画ならどんなものでも好きです、と読み替えたほうが分かりやすいかもしれません。日本映画の作品数でとらえているわけではないので単数形にしないといけないのでしょうね。
ということで some と any の違いをしっかりと押さえておいてください(^^)
2015年
8月
06日
木
疑問文での some と any の違い
先週書いた「some と any の使い分け」の続き。
中学生の英語では「some は肯定文」「any は疑問文や否定文」に使う、と習いますが、全てがそのルールに当てはまるわけではありません。
肯定文で使うことが多い some ですが、疑問文でも使えます。
疑問文に some を使うのは相手が Yes と答えることを期待/想定している場合。
ex.) Do you have some money?
お金、持っていますか?(いくらかは持っていますよね)
これが any だと、
ex.) Do you have any money?
お金、持っていますか?(持っていませんよね)
というように否定的なニュアンスになります。
ですので、疑問文に対する答えに Yes を期待/想定する場合は some を使うのですね。
あとは、人にものをすすめるときも、
ex.) Would you like some coffee?
コーヒーはいかがですか?
Yes を想定しているから some を使います。
some と any のイメージとして、
some → 「ある」ことを想定している
any → 「ない」ことを想定している
というニュアンスの違いがあることを覚えておきましょう。
次回は「肯定文での some と any の違い」について書いていきます(^^)
2015年
8月
05日
水
英語で「先生」って呼ぶには?
今日、小6の子がすららでこんな間違いをしていました。
問題:
彼らは山田(Yamada)先生の生徒ですか。 ※山田先生は男性
解答:
Are they Mr. Yamada teacher's students?
とても素敵な間違いです。
間違えたときこそ学びのチャンスですから!
ということで、今日は英語での「先生」の呼び方について書きたいと思います。
日本では、先生のことを名字+先生で「○○先生」と呼ぶか、単に「先生」と呼ぶか、大体はそのどちらかですね。
日本語の感覚のまま英語にすると、
「○○ teacher!」
とか
「teacher!」
ということになるのですが、英語ではこういう呼び方はしないようです。
英語で先生を呼ぶ時は、
「Mr. Yamazawa!」
というように、男性なら Mr. + ラストネーム、女性なら Ms. + ラストネームで呼ぶのが普通です。
(ラストネーム=名字のことです)
また、気さくな先生が「Please call me ○○(ファーストネーム). ○○と呼んでください」という感じで、ファーストネームで呼んでいいですよ、と言った場合は遠慮なくファーストネームで呼んでしまっていいようです。
(ファーストネーム=名前のことです)
日本では先生を名前で呼ぶことは基本的にしないし、させないので抵抗あるかもしれないですけど。
この辺りは日本語と英語の文化の違いですね。
日本では、
「相手との社会的距離を広げて相手を尊重する」
のが日本語の丁寧表現であるのに対し、
英語では、
「相手との社会的距離を縮めることによって丁寧さを表現する」
という丁寧表現が根付いているんですね。
ということで英語では「○○ teacher!」とは呼ばないようにしましょう(^^)
2015年
8月
04日
火
速さの学習における「距離」と「道のり」の違い
前回 の続き。
さて、「距離」と「道のり」の言葉の違いを勉強したところで、本来のテーマである、
『小・中学生の "速さ" の学習において、「距離」と「道のり」のどちらを用いるべきか』
について考えてみたいと思います。
まず私の考えは、「距離」を使う方が適切、だと感じます。
「速さ」の学習の中では「AとBという二点間の長さ」を考えることもあれば「池の周りだったり、家から学校までといった道の長さ」を考えることもあるわけです。
そのどちらでも使うことのできる「距離」で定義したほうが適切です。
「道のり」とは「道路の距離」に限定した言葉なのだから「AとBという二点間の長さ」というようなことを表わすのには不適切なんですよね。
けれども、どうも学校の教科書では「速さ、時間、道のり」で表記しているようです。
すべての教科書をもっているわけではないので各教科書会社の指導計画作成資料、
東京書籍
http://ten.tokyo-shoseki.co.jp/text/shou/sansu/program.htm
大日本図書
http://www.dainippon-tosho.co.jp/j_school/sansu/archive/guidance_plan.html#no01
学校図書
http://www.gakuto.co.jp/web/jun/junsansu/nenkan/
教育出版
http://www.kyoiku-shuppan.co.jp/view.rbz?cd=2562
啓林館
http://shinko.ee-book.com/h27textbook/math/curriculum/
日本文教出版
http://www.nichibun-g.co.jp/textbooks/sansu/sansu_dl/
を確認してみましたが、ほぼ全ての教科書で「道のり」を使っていました。東京書籍と啓林館のみ「距離」という言葉も使っているようですが、この2社も速さの公式を学ぶところからは全て「道のり」で表記されています。
また、手元に合った教科書「東京書籍:新編 新しい算数6」も確認してみました。
速さの単元はP108~P119で、そのうちP108~P111までは全て「きょり」で表記がされていますが、P112から唐突に「道のり」に変わります。ちょうど公式が登場するところからで、以降は全て「道のり」になっていました。
学校の教科書や準拠ワークなどをみても大体は「道のり」で統一されているようです。
これ、なんで「道のり」になったんでしょうね。「距離」の方が汎用性の高い言葉だと思うのですが。。。
その辺りの経緯なんかも知りたいものです。
さて、ということで結論。
距離と道のりの意味の違いは知っておくべきだが、速さの勉強をする上ではイコールと考えても問題はない
が私の出した答えです。
ここで学ばないといけないことは「速さに関わる数量の関係」を正しく理解すること。
速さと時間から導き出される長さのことを「距離」と「道のり」という記号のどちらで考えたとしても結果は変わらないですし、支障もないです。
なかには表記を統一しないと子どもたちが混乱する、ということをおっしゃる先生もいたりしますが、少なくとも私はその程度のことで混乱するとは思えませんし、そんなことで困っている子どもも見たことはありません。
もし二つの言葉の違いに戸惑う子がいれば、その時は先生が助けてあげればいいだけです。
先生はそういうときのためにいるんですから(^^)
2015年
8月
03日
月
「距離」と「道のり」の意味の違い
すらら導入塾のコミュニティでこんな議論がありました。
『小・中学生の "速さ" の学習において、「距離」と「道のり」のどちらを用いるべきか』
些細なことかもしれませんが、そんな疑問を突き詰めて考える、もっと深く知りたいという知的好奇心に突き動かされた自発的な行動こそが「勉強する」ということだと思っています。
色々と調べてたくさんのことを知ることができたのがとても楽しかったです♪
ということで今回は「距離」と「道のり」の意味の違いについて書きます。
まず、この二つの言葉は小学校3年生の算数ではこのように習います。
・まっすぐにはかった長さを「距離」
・道にそってはかった長さを「道のり」
次に、この二つの言葉の意味を大辞泉で調べてみました。
きょり【距離】
①二つの場所や物事の間の隔たり。
②人との関係で、相手に対する気持ちの上での隔たり。
③数学で、二点を結ぶ線分の長さ。
また、二つの図形上の点を結ぶ線分のうちの最短のものの長さ。
みちのり【道程】
ある地点から他の地点までの道の長さ。目的地までの道路の距離。どうてい。
さて、小3算数習う内容と実際の言葉の意味との間で大きな齟齬は無いように見えますが、決定的な違いが一つあります。
それは小3算数で習う「距離」の定義が「まっすぐな長さ」に限定されてしまっていること。
もちろん「まっすぐな長さ」も「距離」ではあるのだけれど、本来は「まっすぐではない長さ」もまた「距離」なのです。
小3算数で習う内容は、
二つの地点の間を測る方法として「まっすぐに測る方法」と「道に沿って測る方法」とがあるよ。まっすぐに測ったときの長さを「距離」、道に沿って測ったときの長さが「道のり」と区別して覚えよう。
ということです。
「まっすぐ測った長さ」を正しく区別し表現するなら「直線距離」を用いたほうが齟齬は生じないと私は思うのですが、小学3年生の学習ということで長さを測る二つの方法を分かりやすく区別するのに「距離」と「道のり」という言葉を使っているのかもしれません。
「直線距離」を単に「距離」というのも言葉の定義としては正しいですからね。
けれど「距離」と「道のり」の意味を正しく理解させたいなら、やはり「直線距離」という言葉も使って教えてあげたほうがいいような気がします。
ちなみに一応この言葉も大辞泉で調べておきました。
ちょくせんきょり【直線距離】
二点間を結ぶ直線の長さ。平面上の二点間の最短距離。
ということで、まとめると、
二点間の長さを表わす「距離」という大きな概念があり、その中に、「道のり(道路の距離)」や「直線距離(直線の距離)」という言葉がある。
ということだと私は理解しています。
次回は「速さの学習における「距離」と「道のり」の違い」について書こうと思います(^^)
2015年
7月
31日
金
夏休みの宿題より ~some と any の使い分け~
塾では生徒の「夏休みの宿題」の面倒(進捗管理と分からない所の指導)も見ているのですが、せっかくなので、生徒から質問があった問題や、多くの生徒がよく分かっていないポイントなんかを、このブログでも取り上げて解説してみたいと思います。
今日は英語の問題からです。
問題:
次の英文の( )内から適する語(句)を選ぼう。
Ken saw ( some / any ) birds. 健は数羽の鳥を見ました。
Emi didn't have ( some / any ) food. 絵美は少しも食べ物を食べませんでした。
この問題を間違えていた子がいたので取り上げてみたいと思います。
some も any も「いくらかの」という意味の形容詞で「some は肯定文」「any は疑問文や否定文」で使われることが多いです。
なので、上記の問題の解答は、
Ken saw some birds.
Emi didn't have any food.
が正解ですね。
また、否定文の not ~ any は「1つも~ない」と強い否定を表わしていて、同じ意味の形容詞 no と置き換えて、
Emi had no food.
と表現することも出来るので覚えておきましょう。
ということで学校の英語学習としては「some は肯定文」「any は疑問文や否定文」という使い方で覚えておきつつ、それ以外に、
・疑問文でも「人にものをすすめるとき」や「Yes と答えることを期待/想定」する場合は some を使う
・肯定文の any は「どんな~でも」という意味を表わす
という使い方を覚えれば良いと思います。
疑問文における some と any 、肯定文における some と any 、これらの詳しい話はまた次回以降に書いていきたいと思います(^^)
2015年
7月
30日
木
進路を決める上で一番大切なこと
前回 の続き。
進路を決めるにあたって一番大切なこと、それは、
自分で決断する
ということだと私は思っています。
人生とは決断の連続です。
その中でも「中学卒業後の進路」は子どもたちが生きてきた中で初めて迫られる大きな決断です。
こんな言い方をすると腰が引けてしまうかもしれませんが、「大きな」と言ってもこの先の人生で訪れるであろう決断に比べればまだまだ大したことではありません。
だからこそ「自分の頭で考え自分の意志で決断する」ということをちゃんと経験しておいて欲しいと思っています。
「学校の先生に言われたから、親に言われたから、この学校にする」
こんな風に自分の人生の決断を他人のせいにしていると必ず後悔します。
人生の決断に絶対的な正解などありません。
自分が決めた道の先で、その決断が正しかったんだと思える生き方をしてください。
あと、誤解がないように言っておくと「先生や親の言うことを聞くな」と言ってるわけではないですからね。そこは人生の大先輩が言うことなのだからしっかりと聞いて受け止めましょう。その上であくまで決断するのは自分だということ、ですよ。
「本当は A高校に行きたいけど、自分の学力ではいけないから B高校にする」
こんな風に学力が足りないことを言い訳にするのもやめましょう。
学力が足りないなら、その足りない学力を埋める努力をすればいいだけです。
やるだけやってダメなら諦めもつくでしょうが、挑戦することもせずに、やるべき努力もせずに言い訳だけをして逃げるような生き方はしないでください。
大人になった時に「あの時もっと勉強頑張ってれば」と必ず後悔します。
ということで、ここまで子どもたちが抱えているであろう進路の不安が少しでも軽くなればと色々書いてきました。
伝えたいことが上手く伝わるかは分かりませんが、少しでも進路に悩む中3生の励みになってくれれば幸いです(^^)
2015年
7月
29日
水
進路の決め方
前回 の続き。
進路に関して子どもたちが不安を感じたり悩むことといえば「どうやって決めればいいか分からない」ってこともあるんじゃないかなって思います。
なので今回は進路の決め方について書いていきます。
将来の夢、自分のやりたいことを考える
どんな仕事に就きたいのか、どこの大学に進みたいのか、やりたいスポーツはあるか、など自分の将来のヴィジョンについて考え明確なイメージができるなら、そこを軸に考えていくことになります。
けれどほとんどの子は自分の将来にそこまで具体的なイメージを持ってはいないでしょうから無ければ無いで構いません。
とりあえず高校に進んで将来やりたいことを見つける、という感じでも今は全然いいと思います。
学校の情報を集める
どこにどんな学校があるのか、自分のやりたい部活はあるのか、大学への進学実績はどうか、そもそも自分の学力で合格できるのか、など何も知らなければ選びようがありませんよね。
学校の情報は、今であればどこの学校でもホームページを持っているでしょうからネットで調べれば簡単に情報は手に入ります。
あとはオープンキャンパスや体験入学に参加して実際にその学校に行ってみましょう。
公立高校、体験入学一覧
私立高校、オープンキャンパス一覧
最後に「進路を決める上で一番大切なこと」を話しておきます、が、こちらはまた次回としますね(^^)
2015年
7月
28日
火
不安を軽くする方法
前回 の続き。
進路に関する不安は進路が確定するまでは消えないし、不安に思う気持ちがあるからこそ目標に向かって努力をすることができるのだから少しは抱えていた方が良い、と言う話をしました。
とは言え、大きすぎる不安は枷にしかなりません。
ということで今回は中3生向け「不安を軽くする方法」について書いてみます。
1.言葉にしてみよう
不安とは形の無いもの。
形が無いので捉えようがありません。
どう取り扱っていいのかも分からない。
だから、まずは自分の抱える不安を言葉にしてみて下さい。
ノートに自分の気持ちを書き出していってもいいし、親や先生に相談してみるのも良いでしょう。
書いたり、人に話すことで自分が何に不安を感じているのかが具体的になってくると思います。
不安の形が見えてくれば自分の取るべき行動も見えてきますよ。
2.周りを見てみよう
受験や進路のことで悩み、不安な気持ちを抱えているのは自分だけでしょうか。
そんなことはないですよね。
大小はあるでしょうが、同じ学年の友達もみな同様の悩みや不安を抱えているはずです。
他のみんなも、同じように悩みや不安を抱えながら一生懸命努力をしているということに気付くことができれば心はふっと軽くなると思います。
3.自分は他の誰より勉強している!と言い切れるくらい頑張ろう
色々書きましたが進路に関する不安、その根底にあるのは勉強に関する不安、というのが多いのではないでしょうか。
「入試の問題が難しくて全然解けなかったらどうしよう」
「自分以外の受験生が全員自分以上に成績の良い人ばかりだったらどうしよう」
など。
だったら解決するのは簡単。
他の誰より努力して、他の誰よりたくさん勉強すればいいだけですよね。
逆に、勉強せずにゲームしたりテレビを見たりしてダラダラと一日を過ごしてしまうと当然不安は大きく膨らんでいくことになります。
本気の努力は絶対に自分を裏切りません。
在りもしない未来の心配をする暇なんかないくらい受験勉強に没頭してみて下さい。
自分の抱えてた不安なんて気がつけば全部吹き飛んでしまいますから!
さて、進路に関する不安は何も勉強の事だけではないと思います。
「どの学校を選べばいいんだろう?」
そんな悩みも抱えていることでしょう。
ということで次回は「進路の決め方」について書いてみます(^^)
2015年
7月
27日
月
進路に対する不安
前回 の続き。
生徒の中には「最近、進路のことが不安で少し落ち着かない」というような子もいたりします。
ということで今回は子どもたちの進路に対する不安についての考えや対処について書いてみたいと思います。
不安は消せない
さて、結論から言うと実は現時点で不安を消すことは出来ません。
ここでいう不安とは進路のことですよね。
志望校に合格できなかったらどうしよう、とか。
この不安が消えるのは実際に受験が終わって合否の結果が出たときだけです。
だからそれまではこの不安が消えることはありません。
不安があるから頑張ることができる
どんなことでもバランスというものが大切です。
不安も同じ。
不安が大きすぎるのもダメですが、不安が全くないのもダメなものです。
人間は不安に思う気持ちがあるからこそ、その不安を解消するための努力をすることができるし、そんな不安に負けない自分へと成長していくことができるのだと思います。
つまり不安とは前に進むために、成長するために必要なもの。
そう考えれば「不安がある」という状態を深刻に考える必要はなくなりますよね。
不安とは、生きている限り常に付きまとうもの、大切なのはそんな不安とどう上手く付き合っていくか、ということです。
必要以上に不安を大きくしない
進路の不安、などのように不確定な未来に対する不安と言うのは、生きている限り、未来がある限り、そしてその未来を知りえない限り、必ず存在し消すことは出来ません。
どれだけ心配したところで未来が確定するまでは消えないのだから、それまでは気楽にその不安と付き合っていきましょう。
先ほど、不安とは荷物と同じようなもの、と言いましたよね。
旅行に行くとき、荷物のなかに必要なものが足りなければ旅先で困りますよね。だからといって何でもかんでも詰め込み過ぎれば重くなって大変です。
なので必要以上に不安を大きくしないことが大事です。
ということで、次回は「不安を軽くする方法」について書いてみたいと思います(^^)
2015年
7月
25日
土
模試の結果
昨日7/24は、7/12に受けた五木模試の成績表が発送される日、ということで結果を見て安心したり不安になったり、生徒の反応は色々あるのですが、今年の生徒は受験に対して不安を口にする子が多い気がします。
「模試の結果が悪かったらどうしよう」
「受験のことが不安で最近少し落ち着かない」
などなど。
この辺りの悩みに対する向き合い方、考え方について書いてみたいと思います。
まず、模試の結果について。
結果とは過去の事実。もう変えることは出来ません。
なので結果がどうであれ、その事実をまずは受け止めましょう。
けれど心配することは何もありません。まだ受験が終わったわけではなく、模試の結果が出ただけです。志望校の合格判定がE判定だったとしても不合格になったわけでもなんでもないです。現時点での自分の立ち位置が分かった、というだけのこと。
大切なのはその事実をどう捉え、どう行動に変えていくか、ということです。
仮に、模試の結果がE判定だった、とします。
①「もうダメだ、自分には無理だ」と「諦める」
②「受験まで半年ある、こんな判定ひっくり返してやる」と闘志を燃やし必死で「頑張る」
細かい選択肢をあげるとキリが無いので、大きく2つ。
E判定という結果を、諦める言い訳に使うのか、自分を奮い立たせ頑張る材料とするのか。
それは自分の捉え方次第です。
逆にA判定だったとしても、その結果に油断し努力を怠れば受験に失敗する可能性は高くなります。
自分が努力を怠っている間にも他の受験生は努力を続けているのだから当然ですよね。
ですので、模試の結果がどうであれ、大切なのはその結果を努力や行動につなげることです。
E判定?
上等です!
他の誰よりも、全国の中3生のなかで一番だって言えるくらいの努力をしてやりましょう!
次回は「進路に対する不安」について書きたいと思います(^^)
2015年
7月
24日
金
夏休みの宿題より ~I think that の否定文、続き~
塾では生徒の「夏休みの宿題」の面倒(進捗管理と分からない所の指導)も見ているのですが、せっかくなので、生徒から質問があった問題や、多くの生徒がよく分かっていないポイントなんかを、このブログでも取り上げて解説してみたいと思います。
今日は 前回 の続き。
「私はトムは忙しくないと思います」を英語で表現するときの書き方を、
I don't think that Tom is busy.(I don't think + 肯定文)
とするのではなく、
I think that Tom isn't busy.(I think + 否定文)
と表現しても大丈夫なの?、という疑問についてでしたね。
答えとしては「後者の表現も文法的には正しい、けれど英語ネイティブな人たちはほとんど使わない」みたいです。
この例文だと分かりにくいので別の例文を挙げて説明します。
① I think that he isn't kind.
② I don't think that he is kind.
① だと「彼は親切ではない」という印象が前面にでてしまい「彼」を非難するようなニュアンスになるようです。だけど「親切ではない」と感じているのはあくまで自分であって他の人はそう感じていないかもしれないですよね。だから ② のように「少なくとも私は~と思わない」というニュアンスの表現を用いるようです。
他にもこんな例文を見つけたので挙げておきます。こちらはディビット・セイン著『ニッポン人のヘンな英語』からの抜粋になります。
① I think you didn't give me the right change.
② I don't think you gave me the right change.
「お釣りはちゃんと渡したと思いますが」と主張する相手に対して、
① の表現だと「いや、君はお釣りをちゃんと渡していないと思うよ」と怒りを込めて言っている感じ、② は「お釣りをちゃんといただいていないような気がしますが」という感じで相手に気を使いながらこちらの気持ちを伝えるニュアンスになるようです。
同じような表現でも not の位置が違うだけで与える印象はずいぶん変わるのですね。
言葉って面白いですね(^^)
2015年
7月
23日
木
夏休みの宿題より ~I think that の否定文~
塾では生徒の「夏休みの宿題」の面倒(進捗管理と分からない所の指導)も見ているのですが、せっかくなので、生徒から質問があった問題や、多くの生徒がよく分かっていないポイントなんかを、このブログでも取り上げて解説してみたいと思います。
今日は英語の問題からです。
問題:
私はトムは忙しくないと思います。(Tom / think / is / I / busy / that / don't).
この問題を、
I think that Tom is don't busy. ※これは不正解
と書いていた生徒がいました。気持ちは凄く分かります。ですが不正解。
日本語の文だけをみると「私は思います」と「トムは忙しくない」という2つの文を接続詞 that でつなぐ形になるように思えます。
けれど単語の選択肢を見ると否定文の材料として don't を使わなくてはならないので、Tom is busy を否定文にして「トムは忙しくない」という文を作ることができません。
なので I think の方を否定して「私はトムは忙しいと思いません」という形にするんですね。
I don't think that Tom is busy. ※これが正解
日本語の文だけをみて考えるのではなく、文法の正しさもちゃんと考えないといけない問題ですね。
あとは「私はトムは忙しくないと思います」を「私はトムは忙しいと思いません」と読み替えられる国語力も必要になってくるかな。
さて、この問題。
単語の選択肢に don't があるから don't think で否定文にすると説明しましたね。
じゃあもし選択肢の制限がなければ I think that Tom isn't busy. と書いてもいいのか、という疑問が浮かんできませんか?
ということで 次回 はこの疑問について書きたいと思います(^^)
2015年
7月
22日
水
夏休みの宿題より ~○%増えた、減ったの考え方~
塾では生徒の「夏休みの宿題」の面倒(進捗管理と分からない所の指導)も見ているのですが、せっかくなので、生徒から質問があった問題や、多くの生徒がよく分かっていないポイントなんかを、このブログでも取り上げて解説してみたいと思います。
今日は数学の問題からです。
問題:
ある学校の昨年度の生徒数は、男女合わせて650人だったが、
今年度は、男子が3%、女子が4%増えたため、合わせて673人になった。
今年度の男子と女子の生徒数をそれぞれ求めなさい。
連立方程式の問題ですが、式を立てるときに「○%増えた」とか「○%引き」というのを x や y など代数をつかってあらわすのに、どういう式を立てればいいか分からない子が多いみたいです。
さて、この「○%増えた」の考え方ですが、「100人から5%増えた」として考えてみましょう。
100人いたところに100人の5%が増えたのだから、
100 + 100 × 0.05 = 105
これが基本的な考え方ですね。
でも実はもっと簡単な式が書けます。
「人数」ではなく「パーセンテージ」で考えると、元となる人数の100人は「100%」で、そこに「5%」を足すのだから合計で「105%」になるわけですよね。つまり「5%増える」ということは「元の人数の105%になる」ということ。
だからこんな風に計算すればいいわけです。
100 × 1.05 = 105
この考え方さえわかれば x や y などの代数に置き換えても簡単に式が立てられると思います。
ちなみに「○%減る」場合ですが、たとえば10%減ったのなら、100%から10%がなくなるのだから「90%になる」ということ。つまり元の数に0.9をかければいいですね。
ということで「○%増えた、減った」の考え方はしっかり理解しておきましょう(^^)
2015年
7月
21日
火
教育において最も大切なこと
先週、子どもに読書習慣を身につけさせる方法について書きました。
その1. 親が本を好きになろう
その2. 本棚と本を買おう
その3. 読書タイムを作ろう
この3つの共通点から見えてくる、教育において最もたいせつなことについて今日は書きたいと思います。
上にあげた3つ。
これらは「本を読まない子ども」を「本を読むことが好きな子ども」に変えることが目的なわけですが、どの方法も「子ども自身」を変えようとしてない、ということがお分かりになりますでしょうか。
一つ目は「親の行動」を変え、二つ目は「家の環境」を変え、三つ目は「家のルール」を変える内容になっています。
なぜか?
それは「他人を変えることはできない」という現実があるからです。
人が自由に変えることができるのは「自分」だけ。
そして他人に対してできるのは「影響をあたえること」だけです。
つまり、子どもに対して、
「本をたくさん読むようになってほしい」なら、
「子どもが本を読みたくなるような影響を与えられるように自分や自分の行動を変える」しかないんですね。
私が考える、教育において最もたいせつなこと、とは、
「相手を変えようとする」
のではなく、
「相手が変わりたいと思えるよう、自分自身が変わっていく」
ことなのだと思います。
子どもに対して、「~しなさい」という指示・命令を一切せずに、いかにして子どもの行動を変えさせるか。
そんなことに知恵と力を注ぎ、楽しみながら子の教育に取り組んでみて下さいね(^^)
2015年
7月
17日
金
夏休みを楽しむために
近隣の小中学校は大体が今日から夏休みに入ると思います。
子どもたちにとっては待ちに待った夏休み。
けれど親にとっては「子どもが勉強しない」ことへの不安やストレスが増大する期間でしかないことも多いと思います。
夏休みの終わりになって「ほとんど宿題が終わってない」なんてことにならないよう今から対策しておきましょう。
大切なのは一番初めにルールを決めてと学習計画を立てておくこと。
・ルールを決める
夏休みに何のルールも制限もなく子どもを放っておくと学習面だけでなく生活面も大きく乱れていきます。
そうならないためのルールを親子で話し合って決めましょう。
ポイントは親が一方的に決めないこと。
基本的には子どもが自分で考えて決めるようにして下さい。
親がするのは修正と承認だけです。
・学習計画を立てる
夏休みの宿題に取りかかる前に、まずは計画を立てさせましょう。
まずは、いつまでに終わらせるのか、目標を決める。
次にゴールまでの日数と宿題の量を把握、一日にクリアする量を計算して割り振っていきましょう。
あとは毎日進捗管理をして予定通り終わらせられなかった日があれば、すぐに修正、傷が浅いうちにリカバリさせること。
こちらも大事なのは「子どもが自分で考えて決める」ことですね。
夏休みを楽しみ尽くすためにも、自分で決めたルールの範囲内で、やるべきことをきちんとやったうえで、思う存分遊び倒しましょう(^^)
2015年
7月
16日
木
読書習慣が身につく3つの方法、その3
前回 の続き。
子どもに本を読む習慣を身につけさせるための方法、今日は「その3」についてです。
3. 読書タイムを作ろう
家族全員で本を読むためだけの時間を作りましょう。
例えば晩ごはんを食べた後、20:00~20:30は読書の時間にしてしまう。テレビも見ない、音楽も聞かない、ゲームもしない、スマホも触らない。本を読むためだけの時間です。
もちろん子どもだけじゃないですよ。
家族全員の読書タイムです。
とはいえ、本を読むこと自体は強要しないことです。
本を「読まされる」のではなく、あくまで自分の意思で「読もうかな」と思わせるように仕向けてください。
家族みんなが本を読んでいて、他にすること、できることは何もない。
本を読むしかない。
そんな状況であったとしても、誰かに「やらされる」ことと、自分で「する」ことでは意味合いが全く違います。
あと大切なのは継続すること。
三日坊主で終わっては意味がないですよね。
我が家の習慣として、この時間は家族みんなが本を読んでいて当たり前、というくらいに定着するまで頑張ってみて欲しいと思います(^^)
2015年
7月
15日
水
読書習慣が身につく3つの方法、その2
前回 の続き。
子どもに本を読む習慣を身につけさせるための方法、今日は「その2」について書いていきます。
2. 本棚と本を買おう
本を読まない子どもの家には本棚も、そもそも本自体が無い、なんてことも多いように感じます。
親からしてみれば「子どもは本を読まない」から「本をあまり買わない」ということなのでしょう。
でもそれは逆だと思います。
実際は、「本を買わない、家に本が無い」から「子どもは本を読まない」のです。
もちろん本があっても子どもは本を読まないかもしれません。
けれど、そもそも本がなければ子どもが本を読みたいと思っても読めないのですから、まずは家にたくさんの本がある、という環境を作ってあげることはとても大切です。
ということで、まずは子どもと一緒に本屋に行って本を買ってあげましょう。
本を買ってあげる上で大切なことは、
・子どもの読みたい本、気に入った本を買ってあげること
・せっかく買った本を読まなかったとしても気にしないこと
でしょうか。
本棚を子どもが好きな本でいっぱいにしてあげれば、嫌でも子どもは読書好きになりますよ!
さて、では次回、「読書習慣が身につく3つの方法、その3」に続きます(^^)
2015年
7月
14日
火
読書習慣が身につく3つの方法、その1
読書をすることは学力を伸ばす上でとても大切。
もちろん分かってはいるけれど、なかなか本を読むということに気持ちは向かないですよね。
ということで今回は子どもに本を読む習慣を身につけさせるための方法を3つ、提案してみたいと思います。
1. 親が本を好きになろう
自分が本を読みもしないのに、子どもに対して「本を読みなさい」と言ったところで読むようにはならないですよね。
子どもは親の言うことは聞きませんし、親の言う通りには育ちません。
子どもは親のしていることを見て、親のしている通りに育っていくものです。
ですので、子どもに本を読ませようとするのではなく、子どもに読書の習慣を身につけさせたいならまずは自分自身、親の方が本を好きになること、読書家になることです。
子どもを変えようとするのではなく、子どもが変わりたいと思えるような影響を与えてあげることを心がけてみてください。
本を読むのが好きで読書を楽しんでいる親の姿を見ているうちに、子どもの中に「僕も本読みたいな~」っていう気持ちがきっと芽生えてくると思いますよ!
自分自身の教養を高め成長することにも繋がるので、ぜひ試してみてください。
さて、では次回、「読書習慣が身につく3つの方法、その2」に続きます(^^)
2015年
7月
13日
月
勉強の土台になる力
前回 の続き。
たくさんの読書によって培われる、勉強の土台になる力、が「読む力」です。
勉強ができるようになるためには、この「読む力」がとても重要になってきます。
なぜか?
答は簡単です。
どんな教科であれ、問題も、解説も、すべて日本語で書かれていて、問題を解くにも、分からないところを理解するためにも、まずはそれらを読まなければ始まらないからです。
例えば、勉強のできない子、というのは、とにかく「読む」ことをしないし、できません。
「先生、この問題わからん~」と言う子のほとんどはロクに問題を読みもしないまま質問をしてきます。
そして半分くらいの子は問題をちゃんと読ませるだけで解けたりすることも多いです。
また、間違えたときにちゃんと解説を読もうとしないので、同じような問題の繰り返しなのにいつまでたっても解けるようにならないのですが、これも解説をちゃんと読ませるだけで大半の生徒が解けるようになっていきます。
つまり勉強が苦手というようなお子様でも、「読む力」さえあれば大抵の問題はクリアできるはずなんです。
勉強とは、
1. インプット(読む、聴く)
2. 考える、理解する
3. アウトプット(書く、答える)
の繰り返しです。
1. ができずにつまづいていては、当然 2. や 3. に進めるはずがありません。
だから「読む力」というのは勉強をするうえでとても大切になってきます。
そして「読む力」を育てるのに最も有効なのが読書です。
お子様が「勉強ができる子」へと成長して欲しいと願うなら、なにはなくとも読書の習慣が身につくような環境作りに力を注ぐこと。
読書によって勉強の土台となる読む力が身についていれば、あとはやる気の分だけ学力は伸びていきますよ(^^)
2015年
7月
10日
金
読書好き=勉強できる、は本当か
今日は読書と勉強の関係性についてです。
「読書が好きで本をたくさん読む子は勉強ができる」
というイメージを持っている人は多いと思います。これって本当でしょうか?
答えはノーです。
読書と勉強の関係性を正確に表現すると、
「読書が好きで本をたくさん読む子は勉強するための土台となる力が身につく」
ということになります。
つまり、たくさん本を読んだ子は勉強をするための準備ができている、ということ。
読書をしているだけでは、まだ勉強ができるようにはなりません。
勉強ができるようになるためには、あたりまえのことですが、勉強をしなければいけません。
では、勉強をするためには必要なものとは何でしょうか。
ひとつは「勉強をしよう!」という気持ちです。これがなければ始まりませんよね。
そしてもうひとつが勉強するための土台となる力です。
ということで次回は「勉強の土台になる力」についてお話します(^^)
2015年
7月
09日
木
ズルに対する指導、その2
前回 の続き。
③子ども自身に考えさせる
何のためにドリルの問題を解いているのか。
ネットで調べたり、答えを写したり、そんなことで得られるものはあるのか。
自分のやっていることの本質を子ども自身に考えさせること。
たとえば目的が「ドリルを終わらせること」であれば「答えを写す」という行為はとても効率的といえるかもしれません。
けれど本来ドリルを解いていくのは「理解の確認と定着」のため。
だとすれば「答えを写す」ことは全く無意味でデメリットしかもたらさないことは明白です。
なぜこのようなズルをしてはいけないのか?
子どもに対して問いかけ、正しい考えに導いてあげることが大切です。
ということで、子どもがちょっとズルいことをした時の指導についての考えを3つ挙げさせていただきました。参考になれば幸いです。
ズルして楽をする、のではなく、楽をする努力ができる人間に育って欲しいものですね(^^)
2015年
7月
08日
水
ズルに対する指導、その1
前回 の続き。
例えば、英語のドリルを解くのにこっそり翻訳サイトを使ったり、ワークの問題を終わらせるのに解答を見ちゃったり。
そんな「ズルいこと」をした時の指導について、いくつか注意点も含め挙げていきます。
①怒る、きつく叱る
ダメなものはダメときつく叱ることは大切です。
けれど頭ごなしに叱るだけでは、下手をすると逆効果になる可能性もあると思っています。
例えば、すべての生徒の、すべてのズルをひとつ残さず見つけられるでしょうか。
他の子もやっているのに自分だけが怒られた。
今までは気づかれなかったのに今回は見つかったから怒られた。
こういうことがあると「バレなければいい」という歪な考えに至ることも考えられるので、叱り方には注意が必要ですね。
②そもそもズルができないようにする
人間なら誰しも楽ができるなら楽をしたいもの。
問題の答えが手元にあったら、弱い心に負けてつい見てしまうものです。
なら始めからそういう選択肢がなければいいわけです。
パソコンなら学習に必要なサイト以外へのアクセスが出来ないように設定を入れておく、ワークなどの解答は全て親や先生が管理する、など。
ただ、一人で学習を進めるうえでの効率面や利便性の面ではデメリットもでてきますし、ズルが出来ない環境を常に用意できるならそれでいいですが、いざ、ズルができてしまう環境に置かれたときにどうなるか、という心配も残ります。
長くなってきたので、続きは次回「ズルに対する指導、その2」で書いていきます(^^)
2015年
7月
07日
火
ズル
生徒が学習している間、私のやっていることは2つ。
・教室をうろうろしながら、生徒の学習の様子を見て回る
・自席ですらら管理画面から学習の様子をチェックする
そうやって生徒の学習の中身をしっかり把握し、ココが分かってないな、ってポイントを分析して一人ひとり指導しています。
そんな感じで、生徒の周りと自席とをウロウロしながら指導をしているのですが、たまに自席から不意をついて生徒の様子を見に行くとズルをしている子がいたりします。
例えば、昨日は英語のドリルを翻訳サイトを使いながらやっていたりとか(^^;
まぁ、それ自体はそんな大層なことではないですよね。ちょっとズルいことをしてしまうことは誰だってあるでしょう。
けれどズルをする生き方を自分で自分に認めてしまうと、それが癖になってしまい、繰り返しているうちに自分で考える力がどんどん失われてしまいます。
だから大切なのは小さな「ズル」をちゃんと見つけてあげること、そして正しく指導してあげることだと思っています。
ということで、次回は「ズルに対する指導」について書いてみたいと思います(^^)
2015年
7月
06日
月
「角川まんが学習シリーズ 日本の歴史」を買いました

発売前から気になっていて、楽しみにしていた本です。
先日発売されたので早速買ってきました!
私のお気に入りポイントは2つです。
ひとつは、「ケロロ軍曹」の吉崎観音(よしざきみね)、「DEATH NOTE」の小畑 健(おばたたけし)といった有名な漫画家がカバーイラストを手掛けている、ということ。
些細なことかもしれませんが、これらの漫画を知っているだけで「この本ちょっと読んでみようかな」と思わせるきっかけになってくれるかもしれませんよね。
もうひとつは、東京大学 山本博文教授の監修で「歴史の大きな流れをつかむ」ことに重点をおいて構成されている、ということ。
歴史の勉強をするうえで、大きな流れをしっかりと押さえておくのは大事なポイントですね。
まだ全巻は読んでいませんが、小中学生の歴史の勉強には大いに役立つと思います(^^)
2015年
7月
04日
土
国語力の伸ばし方
前回 の続き。
国語力とは「聴く」「読む」「話す」「書く」の4つの力のことです。
では、どうすればこれらを伸ばすことができるのか。
親御さんの多くが、国語のテストの成績をあげること、作文を書けるようになること、に力を注いでいるのではないでしょうか。
けれど、それは間違いだと思っています。
国語のテストの成績も、作文も、どちらも日本語のアウトプットです。
仕事でもテストでも何でもそうですが、結果を出すためにはしっかりとした勉強や情報収集が必要ですよね。
国語力を伸ばすにも、まずはインプットから始めないといけません。
日本語のインプット。
つまり、国語力をちゃんと伸ばしたいならまずは「読み聞かせ」や「読書」から始めてみてください。
遠回りなように感じるかもしれませんが、地頭の基礎がつくられる10才くらいまではとにかくたくさん読書量を積み上げておくことが大切です。
読書量という「学力の土台」がしっかりできてさえいれば、かならず勉強が出来る子に育ちますから(^^)
2015年
7月
03日
金
期末テスト結果
1学期の期末テストの結果が大体出そろったので、ウチの生徒たちの戦績をいくつか紹介したいと思います。
内容はシンプルに「70点以上」と「10点以上UP」した結果のみとします。
中2、英語:47点(12点UP)
中3、英語:59点(25点UP)
中2、英語:73点
中2、数学:79点
中2、数学:77点
中3、数学:82点
中2、理科:80点(28点UP)
中2、社会:83点(23点UP)
今回も成績が上がらなかった生徒は一人もいません!
みな本当によく頑張りました!
Congratulations(^^)
2015年
7月
02日
木
国語力
今日は国語力についてのお話。
たぶん子どもの教育において最も多い悩みが「うちの子は国語が苦手で...」ということではないでしょうか?
お子様の国語力を伸ばしたいと考えている親御さんは多いと思います。
では国語力とはなんでしょう。
私の考える国語力は、
・聴く
・読む
・話す
・書く
この4つの力のことで、この4つがしっかりと身についていることが「国語力が高い」ということだと考えています。
ではどうすれば国語力が身につくのか?
こちらはまた次回。「国語力の伸ばし方」でお話したいと思います(^^)
2015年
7月
01日
水
心機一転
今日から7月、2015年もあっというまに半分が過ぎ去り、下半期のスタートです。
ということで心機一転、さぼりがちだったブログの更新を再開します!
がんばります!
ブログのテーマも「子育て&学力アップの応援ブログ」に変更し気持ちだけプチリニューアルしています。
今後はこのテーマにそって、有益な情報をたくさん発信しいく予定ですので、暇なときにでものんびりお付き合いいただけると幸いです(^^)
2015年
6月
03日
水
中間テスト結果
1学期の中間テストの結果が出そろったので、ウチの生徒たちの戦績をいくつか紹介したいと思います。
内容はシンプルに「70点以上」と「10点以上UP」した結果のみとします。
中3、国語:70点(14点UP)
中2、数学:74点(27点UP)
中2、数学:93点(36点UP)
中3、数学:78点(18点UP)
中2、理科:73点(27点UP)
中3、理科:55点(11点UP)
中3、社会:47点(14点UP)
今回も成績が上がらなかった生徒は一人もいません!
みな本当によく頑張りました!
Congratulations(^^)
2015年
3月
04日
水
テスト勉強を終えて
今日で学年末テストのテスト対策カリキュラムは全て終了。
約1週間という短い期間で、全ての生徒が20~25時間もの時間をテスト勉強に費やしてくれました!
とても印象に残ったのは、テスト勉強を全てやり終えて帰るときの生徒たちの顔でした。
勉強をしている間は、しんどい、、、辛い、、、といった表情をのぞかせながら、けれど途中で諦めたりせず最後まで頑張り抜いたからでしょう。
テスト勉強をやり終えたあとは全員が「やりきった」っていう本当にいい笑顔をみせてくれました。
その笑顔を見たとき、生徒たちにはテストの成績なんてものよりずっと大切な経験を積ませてあげることができたと感じました。
それは、
「しんどいこと、辛いこと、嫌なことから逃げずに、こんなにも頑張ることができるんだ!」
という実感です。
このことは、子どもたちの自信となり大きな力となっていきます。
ただし気をつけないといけないのはテストの結果が返ってきたときです。
自分の頑張りに比べて成績が良くなかったり、そのことで親に怒られたりすると、
「あれだけ頑張っても無駄なんだ」「頑張っても結局怒られるんだ」
と心を閉ざし頑張ることを無意味なことと捉えるようになってしまいます。
ですので、テストの成績だけに囚われずに、子どもの頑張りをちゃんと認め、また次のテストのときも同じように頑張り抜くことができるような言葉をかけて、「頑張る力」を育ててあげて欲しいと思います。
「頑張る力」がちゃんと身につけば成績はあとから勝手についてくるのですから。
2015年
2月
22日
日
おうぎ形の面積の求め方
この土日は学年末テスト前ということで教室の方も臨時開校!
生徒たちは全員が4~5時間ほど勉強してくれて、クタクタになりながらも充実感に満ちた表情で帰っていきました(^^)
さて、そのテスト勉強をしている中で、ある生徒がおうぎ形の面積を求める公式について疑問をぶつけてきてくれたので、今日はその疑問を解決してみたいと思います。
おうぎ形の面積は、
「母線の長さ × 弧の長さ ÷ 2」
という公式で求めることが出来るのですが、その生徒は
「確かこう教わった気がする。あれ?こうじゃなかったっけ?わからん。けどなんとなくこの計算でやってた。」
という感じで、それが正しいかどうかの確証すらないまま使っていたようです(^^;
で、その生徒の疑問というのは、なんで母線の長さと弧の長さを掛けて 2 で割ると面積になるの?、ということでしたので解説してみます。

まず、扇形の 「面積」 や 「弧の長さ」 を求める考え方ですが、「母線 x を半径とする円の面積 or 円周」 から 「おうぎ形の中心角の割合」 を掛けることで求めることができます。
母線 x と中心角 θ が分かっている場合、おうぎ形の弧の長さを求める式は次のようになります。
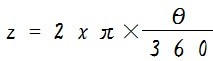
この式を利用して、母線 x と弧の長さ z が分かっていて中心角 θ を求める式を作ると次のようになります。
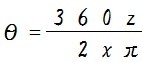
で、扇形の面積は、母線 x と中心角 θ が分かっている場合、式で表すと次のようになります。
(おうぎ形の面積を A とします)
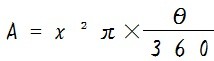
ですが、この式では中心角が分からないと面積は求められないですよね。
けれど、母線 x と弧の長さ z が分かっていれば中心角 θ を求める式が作れましたよね?
なので、これを面積を求める式に代入してみます。
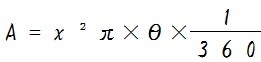

これで中心角が分からなくても母線 x と弧の長さ z さえわかればおうぎ形の面積を求められます。あとはこの式を整理すると、、、
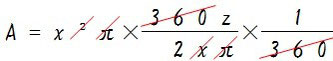
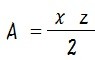
よって、おうぎ形の面積は 「母線の長さ × 弧の長さ ÷ 2」 で求めることができるというわけですね。
2015年
2月
19日
木
円錐の表面積の求め方
今日、生徒が苦戦していた円錐の表面積の求め方について簡単に書いてみたいと思います。

x と y の長さが分かっていて表面積を求めなさい、っていう問題ですね。
立体図形の表面積を求める問題は、立体を平面に、平面を立体に、その図形のイメージを正しく捉えられるか、っていうのが一つのポイントだと思います。
円錐の場合、展開すると、

こんな感じで、おうぎ形と円がくっついた形になります。
それぞれの面積を求めて足せばいいですね。
円の方は 「半径×半径×π」 なので 「y²π」 となります。
おうぎ形の方は、「おうぎ形の弧の長さ」 ÷ 「母線 x を半径とする円の円周」 で円に対するおうぎ形の割合を計算し、円全体の面積からその割合分の面積を求めます。
ちなみに 「おうぎ形の弧の長さ」 は 「半径 y の円の円周」 と同じ長さなのでそこから計算します。
あとはこの二つを足せば円錐の表面積を求めることが出来る、というのが考え方ですね。
さて、ではここで一歩進んで 「もっと楽に求める方法」 について考えてみましょう(^^)
まずは上記の考え方を x と y を使って一つの式として書き出します。(円錐の表面積を A としてます)
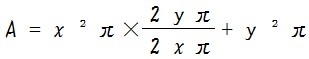
この式を整理すると、
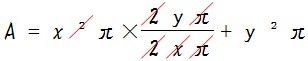
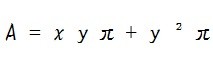
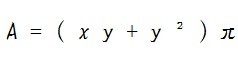
実はこんなに簡単に円錐の表面積を求めることが出来るんですね。
中学一年生の一学期に習った代数の計算を利用すれば複雑な計算も楽に解けてしまうわけです(^^)
とはいえ、この公式を生徒に教えることはしません。
テストの成績を伸ばすことだけが目的ならそれでいいかもせれませんが、本当に伸ばさないといけないのは学ぶ力、考える力です。
子どもたちには、何も考えずただ公式に当てはめて計算をするだけではなく、元となる考え方をきちんと理解してほしいと思っています。
2015年
2月
18日
水
テスト前、1週間の個別カリキュラム
今日から蒲生中学と桜宮中学の学年末テスト1週間前に入りました。
今までは生徒の自主性を重んじ自習による学習を軽くサポートするだけでしたが、今回から一人ひとりの「今日までの学習進捗」「テスト範囲」「目標」を踏まえたうえでテスト対策学習カリキュラムを作成、必要な授業時間数を見積もって追加授業の提案をしています。
生徒にはすこぶる不評ですが(^^;
お母さんには好評です(^^)
テスト前でも家ではほとんど勉強を頑張らないから、、、なんでしょうね。
なにはともあれテストまでのたった1週間の間だけです!
自分のための努力を積み重ねていってほしいと思います!
がんばっていきましょう(^^)
2014年
9月
04日
木
iTunesカードのラインナップって1,500円~なんですね

生徒たちのやる気アップ企画としてやっている「すららレース」の賞品、iTunesカードを買ってきました。
金額は1,000円です。
で、買いに行って初めて気づいたんですがiTunesカードのラインナップって1,500円、3,000円、5,000円、10,000円の4種類で、1,000円のカードって売ってないんですね。
知りませんでした(^^;
で、どうしよう、と思っていたらイオンの携帯ショップで1,000円のカードが3枚入ったマルチパックってのを見つけたのでそちらを購入。
その場で開けて1枚ずつカードをラッピングしてもらいました♪
そのうち1枚を すららレース 1st run 優勝の D君にプレゼント!
生徒たちには、塾内イベントに積極的に参加して残りのカードもどんどん持って帰ってもらいたいと思っています(^^)
2014年
9月
04日
木
[LINE-Log] すらら英語 Stage3 Lesson17
LINEのグループチャットで生徒たちに向け、すららの学習内容をUNIT毎に3~4行程度に要約し発信しています。
その内容をLesson単位でまとめて当ブログに転記しています。
---------------------------------
■S-3 L-17 U-62
「今 何時?」時間の聞き方と答え方
・聞き方
What time is it now? 今、何時ですか?
・答え方
It's five o'clock. 5時です。 / It's ten forty-five. 10時45分です。
答えるときは it を主語にして、It is の後に時間を数字で言う。o'clock は「○時ちょうど」の時に使い、省略しても構いません。
・20以上の数字
21~29は twenty (20) の後に - (ハイフン) と数字 1~9 の単語を付けるだけ。30 以上も同じように作ればいい。
thirty (30)
forty (40)
fifty (50)
sixty (60)
■S-3 L-17 U-63
「今日は何曜日?」曜日の聞き方と答え方
・聞き方
What day is it today? 今日は何曜日ですか?
What day of the week is it today? 今日は(その週の)何曜日ですか?
・答え方
It's Friday. 金曜日です。
答えるときは it を主語にして、It is の後に曜日を言えばいい。
Monday (月曜日)
Tuesday (火曜日)
Wednesday (水曜日)
Thursday (木曜日)
Friday (金曜日)
Saturday (土曜日)
Sunday (日曜日)
■S-3 L-17 U-64
「今日は何日?」日にちの聞き方と答え方
・聞き方
What day of the month is it today? 今日は(その月の)何日ですか?
What's the date today? 今日は何日ですか?
・答え方
It's June 10. 6月10日です。 / It's September twenty-first. 9月21日です。
答えるときは it を主語にして、It is の後に「月」と「日にち」を言えばいい。
Junuary (1月)
February (2月)
March (3月)
April (4月)
May (5月)
June (6月)
July (7月)
August (8月)
September (9月)
October (10月)
November (11月)
December (12月)
「日にち」を言うときは序数 (~番目の) というカタチにしないといけない
first (1番目の)
second (2番目の)
third (3番目の)
fourth (4番目の)
fifth (5番目の)
sixth (6番目の)
seventh (7番目の)
eighth (8番目の)
ninth (9番目の)
tenth (10番目の)
eleventh (11番目の)
twelfth (12番目の)
thirteenth (13番目の)
fourteenth (14番目の)
fifteenth (15番目の)
sixteenth (16番目の)
seventeenth (17番目の)
eighteenth (18番目の)
nineteenth (19番目の)
twentieth (20番目の)
thirtieth (30番目の)
21~29は twenty (20) の後に - (ハイフン) と序数 1~9 の単語を付けるだけ。30 以上も同じように作ればいい。
例) twenty-first 、twenty-fifth など
2014年
9月
03日
水
誕生日☆0830☆
アチーブメントでは生徒の誕生日に心ばかりのプレゼントを贈ります。

中学生の女の子、ということで LUSH の「みつばちマーチ」 を買ってきました。思わず食べてしまいそうになるくらい甘い香りの石鹸です♪
毎日 勉強を頑張っている子どもたちへのささやかなご褒美です♪
Mさん!
誕生日おめでとう!!
2014年
9月
03日
水
[LINE-Log] すらら英語 Stage3 Lesson16 (その3)
LINEのグループチャットで生徒たちに向け、すららの学習内容をUNIT毎に3~4行程度に要約し発信しています。
その内容をLesson単位でまとめて当ブログに転記しています。
---------------------------------
■S-3 L-16 U-58
助動詞 must を置き換える表現
[語順] ( 主語 + must + 動詞の原形 + ~. )「~しなければならない」
↓
[語順] ( 主語 + have to + 動詞の原形 + ~. )「~しなければならない」
"must" は "have to" に置き換えられる。主語が3人称単数の場合は "has to" になる点に注意!
例) He has to take this medicine. 彼はこの薬を飲まなければならない。
否定文/疑問文は一般動詞の文と同じルールで作ればいいよ (ただし否定文は訳の意味が変わってくるので注意!詳しくは次のunitで勉強するよ~)
例) Does he have to take this medicine? - Yes, he does. / No, he doesn't hove to.
■S-3 L-16 U-59
助動詞 must の否定文を置き換える表現 (must not ≠ dont't have to)
[語順] ( 主語 + must not + 動詞の原形 + ~. )「~してはいけない」
[語順] ( 主語 + don't have to + 動詞の原形 + ~. )「~する必要はない」「~しなくてもよい」
→主語の人称によって don't と doesn't は使い分けること!
例) You don't have to speak Japanese. あなたは日本語を話す必要はない。
■S-3 L-16 U-60
助動詞 shall の文 (Shall I ~ / Shall we ~ の2つの疑問文だけ覚えればいいよ)
[語順] ( Shall I + 動詞の原形 + ~. )「~しましょうか」→相手に申し出る表現
例) Shall I open the window? 窓をあけましょうか?
- はい、お願いします。 Yes, please.
- いいえ、結構です。 No, thank you.
[語順] ( Shall we + 動詞の原形 + ~. )「~しませんか」→相手を誘う表現
例) Shall we play tennis? テニスをしませんか?
- ええ、しましょう。 Yes, let's.
- いいえ、やめておきます。 No, let's not.
■S-3 L-16 U-61
助動詞の表現を2つ組み合わせた文の作り方
【助動詞のルール】助動詞は2つ続けて使うことができない!
「~することができるでしょう」
→will can ~ という使い方は NG なので、「will ~でしょう」+ can と同じ意味の「be able to ~できる」を組み合わせる
例) You will be able to speak English well. 君は上手に英語を話せるようになるでしょう。
「~しなければならないでしょう」
→will must ~ という使い方は NG なので、「will ~でしょう」+ must と同じ意味の「have to ~しなければならない」を組み合わせる
例) You will have to do your homework. 君は宿題をしなければならないでしょう。