生徒たちの「分からない」を取り上げて考えていきます。

解き方が分からない前提で「どんな風に考えて解いていくか」という過程を書いていくので、ぜひご自身でも解き方を考えながら読み進めてみてください。


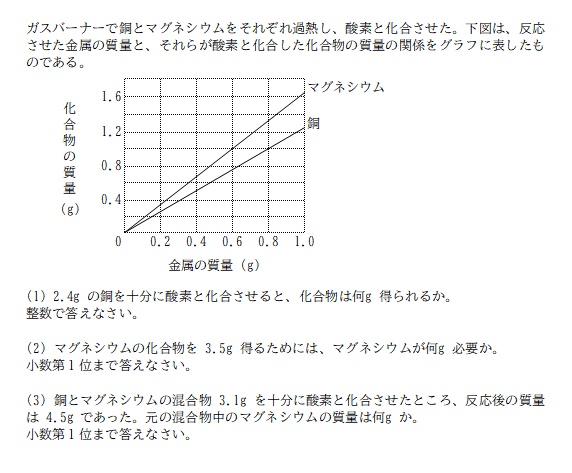
今回は、とある中学の授業で出されたプリントからの出題、理科(2年、化学) の問題です。

 

 

昨日の記事（「分からない」を考えよう！ #11）を読んで「分かった！」と思えたなら解ける問題です。

 

勉強は「分かった！」と思っただけでは終わりではありません。「分かった！」と思ったなら、それが本当なのかどうかを確認し「分かった！、ということを証明する」ところまでやってはじめて勉強したといえます。

 

本当に「分かった！」のか、「分かった気になった」だけなのか、その確認のためにもぜひチャレンジしてみてください。

 

 

(1)

 

グラフから必要な情報を読み取ります。

縦線と横線の交点を銅のグラフが通る場所を探すと、金属の質量 0.8g / 化合物の質量 1.0g の点を通っていることが分かる。

 

銅 0.8g が酸化し、酸化銅 1.0g ができているので、この値を整数の比に整理する。酸素の質量については特に考える必要はない。

 

　銅：酸化銅 = 0.8：1.0

　　　　　　 = 8：10

　　　　　　 = 4：5

 

この比率を利用して銅 2.4g に対する酸化銅の質量を求めれば良い。

 

　銅：酸化銅

　4：5 = 2.4：x

　4x = 12

　x = 3

 

A. (1) 3.0g

 

 

(2)

 

これも先の問題同様、グラフから必要な情報を読み取ります。

縦線と横線の交点をマグネシウムのグラフが通る場所を探すと、金属の質量 0.6g / 化合物の質量 1.0g の点を通っていることが分かる。

 

マグネシウム 0.6g が酸化し、酸化マグネシウム 1.0g ができているので、この値を整数の比に整理する。酸素の質量については特に考える必要はない。

 

　マグネシウム：酸化マグネシウム = 0.6：1.0

　　　　　　　　　　　　　　　　 = 6：10

　　　　　　　　　　　　　　　　 = 3：5

 

この比率を利用して酸化マグネシウム 3.5g の元になったマグネシウムの質量を求めれば良い。

 

　マグネシウム：酸化マグネシウム

　3：5 = x：3.5

　5x = 10.5

　x = 2.1

 

A. (2) 2.1g

 

 

(3)

 

銅と酸化銅、マグネシウムと酸化マグネシウム、それぞれの比率を元に考える。

 

　銅：酸化銅 = 4：5

　マグネシウム：酸化マグネシウム = 3：5

 

酸素については「十分に酸素と化合させ」と記載があるので、特に考える必要はないです。上記比率をそのまま質量と考え、銅とマグネシウムの混合物が 3.1g、酸化銅と酸化マグネシウムの混合物が 4.5g になるように考える。

 

ここからは分かりやすいように、

 

　銅とマグネシウムの混合物 3.1g → 31g

　酸化銅と酸化マグネシウムの混合物 4.5g → 45g

 

というように 10倍した値で考ることにします。

 

銅+マグネシウムが 31g (奇数) ということは、銅 (偶数) + マグネシウム (偶数) という組み合わせにはならないことが分かる。銅「4」は何倍しても偶数なので、マグネシウム「3」の方を奇数にするよう考える。

 

銅：酸化銅、マグネシウム：酸化マグネシウム、の比率をそのまま質量として、銅とマグネシウムの混合物 31g、酸化銅と酸化マグネシウムの混合物 45g になる組み合わせを探していく。

 

　マグネシウム：酸化マグネシウム = 3g：5g

 

　　11倍すると 33g：55g → どちらも問題文にある値を超えるので NG

 

　　9倍すると 27g：45g → これだと酸化マグネシウムが問題文にある値を超えるので NG　

 

　　7倍すると 21g：35g

　　　→ (銅：酸化銅 = 4g：5g) を 2.5倍した (10g：12.5g) を混ぜ合わせると

　　　　31g：47.5g となるので NG

 

　　5倍すると 15g：25g

　　　→ (銅：酸化銅 = 4g：5g) を 4倍した (16g：20g) を混ぜ合わせると

　　　　31g：45g となるのでこの割合で混ぜ合わせるのが正解！

 

となり問題文と合致する質量を求めることができましたね。31g と 45g は本来の質量を考えやすいように 10倍にした値なので、

 

　銅：酸化銅 = 1.6g：2.0g

　マグネシウム：酸化マグネシウム = 1.5g：2.5g

 

で混ざり合っていると考えることができる。よって元の混合物中のマグネシウムの質量は、

 

A. (3) 1.5g

 

 

いかがでしたか？

 

 

前回の記事を読んで、その問題を解く考え方をちゃんと理解できていたなら、今回の問題も解くことができるはずです。

 

解くことができないということは、残念ながら前回の記事の問題を「ちゃんと理解できていなかった」可能性が高い、ということになります。

 

最初にも書きましたが、「分かったと思う」ことがひとつの勉強のゴールではないです。「分かったと思ったことを、本当に分かったのか確認し証明する」ことまでやってはじめてひとつの勉強のゴールだと言えるのです。

 

問題が解けて分かったと思えたなら、必ずその類題を探してチャレンジするようにしてくださいね！

 

 

-----

 

問題を解けば終わり、答えが分かれば終わり、ではなく、問題を解く過程でたくさんの「なんだろう？」っていう疑問を見つけて、それを理解していく努力が勉強です。

そしてその「なんだろう？」を解き明かしたときの達成感を味わうのが勉強の醍醐味です！

ぜひたくさんの「分からない」を見つけて、それを「分かった！」に変えていく努力をしていってくださいね！

 

 
以上です。お疲れさまでした！
(*ᴗˬᴗ)⁾⁾