生徒たちの「分からない」を取り上げて考えていきます。

解き方が分からない前提で「どんな風に考えて解いていくか」という過程を書いていくので、ぜひご自身でも解き方を考えながら読み進めてみてください。

 

今回は、とある中学の「3年 1学期 実力テスト」で出題された、数学の問題です。

 

 

 

(1) は簡単ですね。平均値とは、値の合計を値の数で割ったものです。なので、

 

(186+182+178+172+168)÷5

=886÷5

=177.2

 

　A. (1) 177.2 cm

 

 

となります。ここは簡単。

 

 

さて、質問があったのは (2) ですね。この問題は解を考えるときに見落としやすいポイントがある、のかもしれないですね。考えてみてください。

 

Let's think!

 

まず、問題文の中にある「メジアン」という言葉。

これは「中央値」のことですね。

 

 

ちなみに、なぜ「平均値」は日本語の言葉を使うのに、「中央値」は日本語ではなく英語の言葉を使うのか、が個人的には疑問だったりするのですが、何か理由があるのかな？

 

まぁ、それは別にいいとして。

 

 

中央値 (メジアン) ：値を小さい順に並べて、ちょうど中央にある値のこと。

 

 

具体例、まずは値の数が奇数のとき。

 

次は値の数が偶数のとき。

 

と、中央値はこのように求めます。では中央値について理解したところで問題について考えていきましょう。

 

 

 

d の体重が分からないので、他の 4人の体重を並べてみます。

 

　64 , 72 , 75 , 80

 

ここのどこかに d の体重 x kg が入るわけですが、x がどこに入ったとしても両端の 64 と 80 が中央値になることはなさそうですね。

中央値となる可能性があるのは 72 か 75、あとは d の体重 x の 3 パターン。

 

実際に x に色々と数値を当てはめて見ていきましょう。

 

このように、

 

「x が 72 以下ならどこに入ったとしても中央値は 72」

「x が 75 以上ならどこに入ったとしても中央値は 75」

 

であることが分かりますね。あとは、

 

「x が 72 より大きく 75 未満で中央値は x」

 

となるパターンです。

 

よって、中央値として考えられるのは「72 , 75 , x」の 3通り！と考えてしまうと不正解になるので、ここが気を付けなければいけないポイントかな、と思います。

 

せっかくなので、答えが 3通りだと思ってしまった人は、ここで一度考えてみましょう。

 

Let's think!

 

中央値 x を考えるときに気を付けなければいけないポイント、それは、x が取りうる値はひとつだけか？、ということですね。

 

「x が中央値になる場合」

 

で考えを止めず、

 

「x が中央値になる場合、x に当てはまる値は何があるか」

 

まで考えないとダメですね。

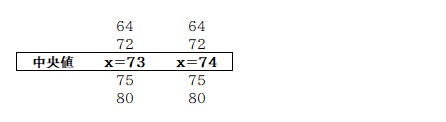
このように x が中央値になる場合、x に当てはまる値は 73 と 74 の 2通りが考えられます。

 

よって中央値として考えられるのは「72 , 75 , x (73 , 74)」の 4通りとなります。

 

　A. (2) 4通り

 

 

分からないと質問があったのはこの問題だけですが、せっかくなのでここでは最後の (3) も考えてみましょう。

 

Let's think!

 

まずは、誤った値のままの場合の中央値と、正しい値に基づき修正された中央値 (182) について考えてみます。

 

 

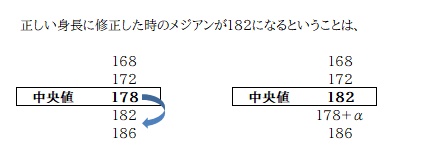
修正前の中央値は 178 で、修正後 182 になったということは、

 

「168/172/178 のいずれか (おそらく178) が誤りで、正しい数値は 182 より大きい」

 

ということが考えられますね。

 

 

では次に平均値について考えてみます。

 

(1) の解より 5人の身長の平均値は 177.2 だがこれが誤りで、正しい数値に基づく 5人の身長の平均値は 178.2 となる。

 

平均値(誤) と 平均値(正) の差は 178.2-177.2=1 なので、5人の平均が 1cm 増えたということは、身長の合計が 5cm 増えたということ。

 

5人の身長のうち、5cm 増えることで 182 より大きくなるのは、と考えれば答えが分かりますね。

 

　A. (3) 誤っている値 178 cm / 正しい値 183 cm

 

 

 

ちなみに補足。

上記で、誤った値を 168/172/178 のうち 178 がおそらくそうであると考えた理由。

分かりますか？

 

もし 168 が誤りで正しい数値が 182 より大きくなる場合を考えると、168 だけでなく 172 と 178 も正しい数値が 182 より大きくなる可能性が出てきて、168/172/178 のうちどれが誤った値なのかを特定することができなくなります。

 

なので正しい平均値から具体的に何 cm 変化があったのかの計算をする前に、誤った値はおそらく 178 かな、と考えたということです。

 

 

問題をただ解くだけでなく、問題を解く過程でこんな風にいろいろ考えることが論理的な思考力を養っていくことにつながります。

少しでも楽に解くにはどうすればいいか、だとか、ちょっとの疑問でもトコトン考える！そういう勉強を心がけてください。

 

-----

 

問題を解けば終わり、答えが分かれば終わり、ではなく、問題を解く過程でたくさんの「なんだろう？」っていう疑問を見つけて、それを理解していく努力が勉強です。

そしてその「なんだろう？」を解き明かしたときの達成感を味わうのが勉強の醍醐味です！

ぜひたくさんの「分からない」を見つけて、それを「分かった！」に変えていく努力をしていってくださいね！

 

以上です。お疲れさまでした！
(*ᴗˬᴗ)⁾⁾