生徒たちの「分からない」を取り上げて考えていきます。

解き方が分からない前提で「どんな風に考えて解いていくか」という過程を書いていくので、ぜひご自身でも解き方を考えながら読み進めてみてください。

今回は、とある中学のワークからの出題、数学(2年 連立方程式) の問題です。

連立方程式の文章問題。特別難しいというわけではありませんが、割合の計算、その考え方をきちんと理解していないと解けません。

この記事の投稿時はちょうど１学期の期末テスト前なので、２年生はしっかり勉強してテストに備えておきましょう！

あと、この問題は連立方程式の問題として出題されていますが、一次方程式でも解くことができます。なので１年生もぜひチャレンジしてみてください。

Let's think!

解ける子はすぐ解けたと思います。

分からない！って子は一緒に考えていきましょう。

文章問題を解くコツは、提示された情報をきちんと整理して考えること。

整理すべき情報はまず３つ。

「男子の数」「女子の数」「全体の数」

これら３つの情報をさらに、

「昨年度」「今年度」

の２つの軸でそれぞれ考える必要がありますね。

私が教えるときは次のように書いて考えさせます。

こういう感じの簡単な表に、問題文に書かれている情報、何を x や y といった文字に置き換えるか、を書き込みながら整理していきましょう。

Let's think!

問題文から分かっていること。

・昨年度の生徒数は、男女合わせて 650人

・今年度は、昨年度と比べて、

　　- 男子が 4%減った

　　- 女子が 6%増えた

　　- 全体で 4人増えた

これを表に書き込みます。

このように整理することができます。

なので昨年度の男子と女子の数を文字に置き換えて考えるのが良さそうですね。

昨年度の男子の数を「x」、女子の数を「y」としましょう。

では次に今年度のところを考えていきます。

合計は 650人から 4人増えた、ということなので 654人ですね。

問題は男子の数と女子の数。

ここを文字を使った数式に置き換えましょう。

Let's think!

ここから少し「問題を解く」という本筋から逸れますが、「問題を解く」ために必要な考え方を学ぶために寄り道しましょう。

割合の計算について。

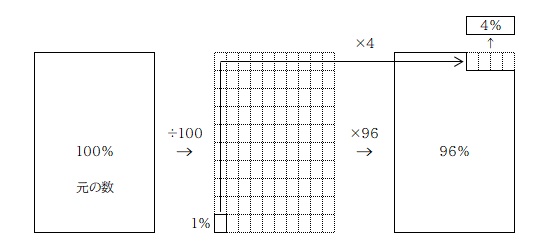
これが問題文にある「4%減った」の考え方。

「4%減る」ということは「96%になった」と言い換えることができるので、「100 を 96 にする」という考え方がひとつ。

計算の仕方は次の通り。

もうひとつは「100 の中の 4 を求めて、元の数から引く」という考え方。

計算の仕方は次の通り。

二通りの考え方、その違いは、

前者は、百分率の状態で 100% から 4% を引いて考えていて、

後者は、元の数の 4% の数を求めて実際の数を引いている、

つまり 4% を減らす計算を「百分率の状態でする」か「実際の数でする」かという違いですね。考え方としては両方理解しつつ、計算については前者の方法を身につけましょう。そのほうが簡単だし扱いやすいです。

ここまでの説明の「元の数」を「1200円」として例を挙げておきます。

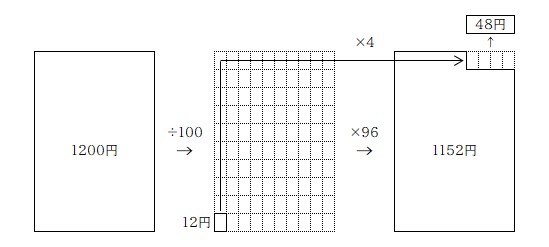
1200円の 4%：　1200×0.04=48円

1200円の 4%減（96%）：　1200×0.96=1152円

スーパーでよく見る「20%OFF」とか「4割引き(40%引き)」なんかも同じように計算できますので、いろいろ試してみてください。

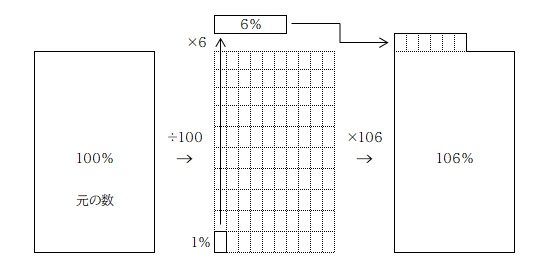
今度は問題文にある「6%増えた」の考え方。

「6%増える」ということは「106%になった」と言い換えることができるので、「100 を 106 にする」という考え方がひとつ。

計算の仕方は次の通り。

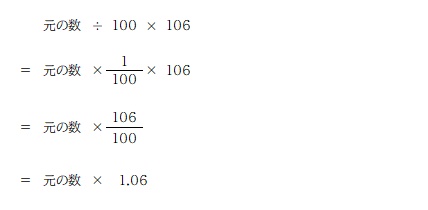
もうひとつは「100 の中の 6 を求めて、元の数に足す」という考え方。

計算の仕方は次の通り。

二通りの考え方、その違いは、

前者は、百分率の状態で 100% に 6% を足して考えていて、

後者は、元の数の 6% の数を求めて実際の数を足している、

つまり 6% を増やす計算を「百分率の状態でする」か「実際の数でする」かという違いですね。考え方としては両方理解しつつ、計算については前者の方法を身につけましょう。そのほうが簡単だし扱いやすいです。

ここまでの説明の「元の数」を「1200円」として例を挙げておきます。

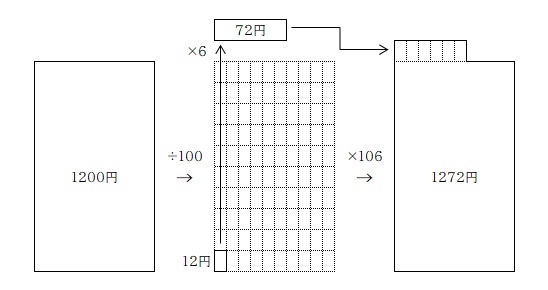
1200円の 6%：　1200×0.06=72円

1200円の 6%増（106%）：　1200×1.06=1272円

身近なものなら消費税が同じように計算できますので、いろいろ試してみてください。

さぁ！割合の計算について「なるほど！」って思える勉強はできましたか？

理解できたと思えたなら問題の続きにチャレンジしてみましょう。

今年度の男子と女子の数を文字を使った数式で表してみましょう。

Let's think!

昨年度の男子の人数が x人で今年度は 4%減ということは、昨年度の人数を 100% としたときに今年度の人数は 96% になった、ということ。

x人の 100分の 96 なので、0.96x と表すことができます。

昨年度の女子の人数が y人で今年度は 6%増ということは、昨年度の人数を 100% としたときに今年度の人数は 106% になった、ということ。

y人の 100分の 106 なので、1.06y と表すことができます。

最後に、男子と女子の数の和が合計になるので、

これで方程式がふたつ完成したので連立方程式で解くことができますね。あとは計算だけですが、せっかくなのでやってみてください。

Let's think!

計算の途中で、計算を楽にするポイントもあったりするので説明していきます。

加減法で解いていきます。まずは②の式を100倍して少数をなくします。

次に①の式を 96倍して、②´の式と x の項を揃えます。

ここで計算をちょっと楽にする方法を。

　650×96

ここの計算、生徒のノートを見るとたいていは真面目に筆算で計算しているのだけれど少し工夫すると暗算で簡単にできちゃいます。

96 をそのまま使うのではなく 96 = (100-4) に変形して計算してみましょう。

そうすれば、

　650×96

　　↓

　650×100=65000

　650×4=2600

　65000-2600=62400

というように暗算でもできる簡単な計算３つで終わらせることができます。650 と 96 の掛け算を暗算でするのはちょっとしんどいですよね。

ぜひ取り入れて実践してみてください。

さて、計算の続き。②´の式から①´の式を引いて y を求める。

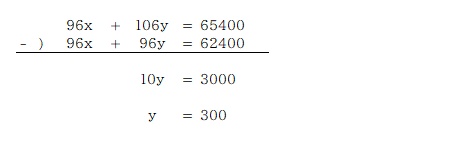
y を①の式に代入し x を求める。

　A. 昨年度の男子：350人、女子：300人

数学の文章問題って苦手な子が多いけど、提示された情報をきちんと整理し理詰めで考えれば実はそこまで難しことではないと思っています。

この問題の場合、割合の計算が分からない、なんて子も多いかもしれませんが、そこもきちんと理解し、何度も実践して自在に扱えるようにしてしまえば何てことはありません。

分からないことをほったらかして逃げずに、ちゃんと分かるまで考えて自分のものにしようとする努力をしていきましょう。

----

最後におまけ。連立方程式を使わず解く考え方について。

連立方程式ではないので使う記号はひとつだけ。昨年度男子の数を x とします。男女の合計が 650人だから女子の数を 650-x というように表すことができますね。あとはそれらの数式から今年度の人数を表す数式を書いてあげれば完成。方程式③を解くだけです。

ちなみにこれって、

式① x+y=650 を変形、y=650-x とし、式②に代入している

ということ。つまり連立方程式を代入法で解いているのと同じことなんですよね。違いは、式をふたつ作ってから代入するか、式を作るときに代入した形のものを作るか。

そう考えると実は１年生の方程式の問題を解いているときすでに、連立方程式の代入法のようなことをやって問題を解いていたんですね。

色々考えてみると新しい発見が見つかって面白いかもしれませんね。

問題を解けば終わり、答えが分かれば終わり、ではなく、問題を解く過程でたくさんの「なんだろう？」っていう疑問を見つけて、それを理解していく努力が勉強です。

そしてその「なんだろう？」を解き明かしたときの達成感を味わうのが勉強の醍醐味です！

ぜひたくさんの「分からない」を見つけて、それを「分かった！」に変えていく努力をしていってくださいね！

以上です。お疲れさまでした！
(*ᴗˬᴗ)⁾⁾