
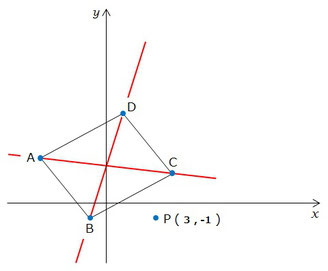
右の図のように、
直線①:y=x/2
双曲線②:xy=6 (x>0)
2点 A(-4,3) B(-1,-1)
がある。
また、四角形ABCDが平行四辺形となるように、2点 C , D をそれぞれ①、②の上にとる。次の問いに答えなさい。
(1) 2点 C , D の座標をそれぞれ求めなさい。
(2) 点P (3,-1) を通る直線n で、平行四辺形ABCDの面積を2等分したい。
直線n の式を求めよ。
--------------------------------------------------
前回は、
「平行四辺形ABCD の中心(対角線の交点)を軸にして、点P と点対称になる点」
について考え、その点と 点P を結ぶ直線を求めました。
ちなみに、
「この直線がどうして 平行四辺形ABCD の面積を二等分する線になるのか?」というと、
点対称になる点同士を結ぶ
↓
点対称の中心を通る
↓
点対称の中心は、平行四辺形ABCD の中心(対角線の交点)
となり、「平行四辺形の中心を通るから」が答えですね。
平行四辺形を二等分する直線 = その平行四辺形の中心(対角線の交点)を通る直線
今回はこの考え方で問題を解いていきたいと思います。
まずは 平行四辺形ABCD の対角線の式を求めていきます。
(1) の問題を解いていれば 点A ~ 点D の座標は全部分かっているはずなので、
点A と 点C の座標から 直線AC の式を求める
点B と 点D の座標から 直線BD の式を求める
一次関数の式 y=ax+b にそれぞれの座標を代入して連立方程式で解けば良いですね。

直線AC と 直線BD の交点の座標を求める
この座標が対角線の交点、つまり 平行四辺形ABCD の中心ですね。

最後に、
平行四辺形ABCD の中心の点 と 点P を結ぶ 直線n の式を求める
となります。
前回の解き方よりかなり手順が多いですね。全部で連立方程式を4回も解かないといけません。と、考えると面倒なだけのように思うかもしれませんが、「入試に向け連立方程式の計算の復習も出来る」と捉えればこちらの解き方を選ぶことにも価値が生まれますね。
全ては捉え方次第。
ぜひ色々な考え方で問題を解き数学を楽しんでください(^^)







