生徒たちの「分からない」を取り上げて考えていきます。

 

解き方が分からない前提で「どんな風に考えて解いていくか」という過程を書いていくので、ぜひご自身でも解き方を考えながら読み進めてみてください。

 

 

今回は、とある中学の「2年 1学期 期末テスト」で出題された、数学 (連立方程式) の問題です。

 

 

 

これもそんなに難しい問題ではないですね。それでも、数学を「解き方」でしか考えられない場合、当然「解き方」を知らなければ解けない、どうすればいいか分からない、となってしまいます。

 

数学の文章問題は「解き方」なんて知らなくても「文章を読んで、情報を整理し、考える」ことさえできれば解くことができるので、仮にこの問題の「解き方」を知っていたとしても、それは一旦横に置いておいて、自分で考えて解いてみてくださいね。

 

 

-----

ではまず、問題文で提示されている情報を整理してみましょう。

 

　・100円玉が何枚かある。枚数は不明。金額は 枚数×100 で表すことができる。

　・500円玉も何枚かある。枚数は不明。金額は 枚数×500 で表すことができる。

　・これら全部合わせると 4800円になる。

 

そのお金を両替した。

　・100円 1枚 → 50円 2枚に、つまり枚数は 2倍になる。

　・500円 1枚 → 100円 5枚に、つまり枚数は 5倍になる。

　・両替後の 100円玉の枚数は、両替後の 50円玉の枚数より、9枚多い。

　　言い換えると「100円玉の枚数」引く「50円玉の枚数」が「9枚」ということ。

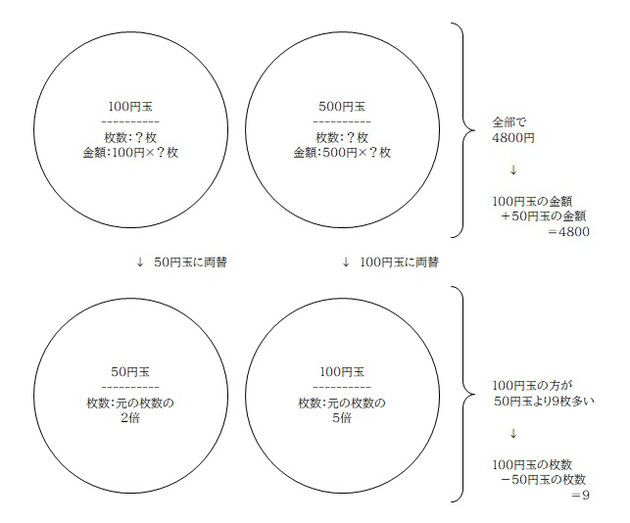
こんな感じでしょうか。これを数式にするために分からない値を記号に置いて考えます。問題の (1) で「x枚の 100円玉」と記述があるので、

 

元の 100円玉の枚数：x枚

元の 500円玉の枚数：y枚

 

とし、整理します。

 

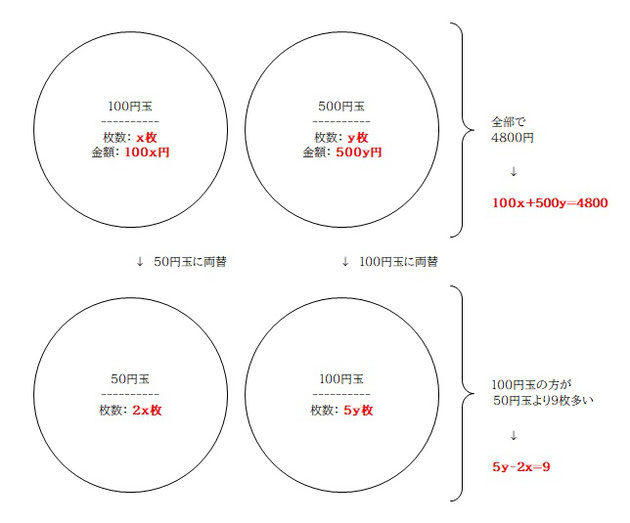
ここまで整理すればあとはただの計算問題ですね。

 

 

-----

 

(1)

 

この問題の肝は両替後の枚数をきちんと数式で表すことができるかどうか。わざわざ小問でそこの確認をさせてくれています。

 

問題文を読んで情報の整理をしっかりとしていればすでに答えは出ていますね。

 

A. (1) 2x

 

 

-----

 

(2)

 

この問題も、すでに方程式ふたつ完成しているのであとは解くだけ。

 

元の 100円玉の枚数：x枚

元の 500円玉の枚数：y枚

 

としているので x , y の値を求めればそれがそのまま答えですね。

 

　100x+500y=4800 ･･･ ①

　5y-2x=9 ･･･ ②

 

解き方は色々、どう解くのも自由ですが、なるべく大きい数字は扱わないほうが楽なので、まずは①の式を 100 で割って、

 

　x+5y=48

 

これを 2倍します。

 

　2x+10y=96 ･･･ ①´

 

②の式は x と y の項の並びが逆なので、これも整理して、

 

　-2x+5y=9 ･･･ ②´

 

x の項がプラスとマイナスなので①´と②´を足して連立方程式を解きます。

 

　2x+10y=96

　-2x+5y=9

 

　15y=105

　y=7

 

これを①´に代入。

 

　2x+70=96

　2x=26

　x=13

 

A. (2) 100円玉：13枚、500円玉：7枚

 

 

 

そういえば文章問題って答えが正しいかどうか、確認することもできます。求めた答えで問題文の通りになるかを確認するだけ。

 

　100円玉 13枚 → 1300円、500円玉 7枚 → 3500円

　金額を合計すると 4800円

 

　100円玉 13枚を 50円玉に両替 → 26枚、500円玉 7枚を 100円玉に両替 → 35枚、

　35-29＝9 で、両替後の 100円玉の方が 9枚多い

 

すべて問題文の条件を満たしていますね。

 

求めた解に自信がなければ、こうやって確認するといいですよ！

 

 

-----

問題を解けば終わり、答えが分かれば終わり、ではなく、問題を解く過程でたくさんの「なんだろう？」っていう疑問を見つけて、それを理解していく努力が勉強です。

 

そしてその「なんだろう？」を解き明かしたときの達成感を味わうのが勉強の醍醐味です！

 

ぜひたくさんの「分からない」を見つけて、それを「分かった！」に変えていく努力をしていってくださいね！

 

 

以上です。お疲れさまでした！
(*ᴗˬᴗ)⁾⁾