生徒たちの「分からない」を取り上げて考えていきます。

解き方が分からない前提で「どんな風に考えて解いていくか」という過程を書いていくので、ぜひご自身でも解き方を考えながら読み進めてみてください。

今回は、とある中学の「2年 1学期 期末テスト」で出題された、数学 (連立方程式) の問題です。

「速さ」の計算は苦手な子が多いイメージですが、いろんな単元の文章問題に登場してくるので、分からなかったり不正解になったときにきっちり見直しをして理解しておくようにしましょう。

数学だけでなく理科でも速さの計算はたびたび登場するので、きちんと理解しておくと様々な場面で勉強が楽になると思いますよ。

-----

ということで、まずは問題を解く前に速さの計算について。

中学生なら「みはじ」などで公式を覚えるのではなく、それぞれの計算の意味を理解しておきましょう。

「速さ」は、単位時間あたりに進む距離を表しています。

つまり、1分あたり何メートル進む、だとか、1時間あたり何キロメートル進む、といった感じですね。

例えば、350m 進むのに 7分かかった場合、350 を 7 で割れば 1分あたり何メートル進むのかを求めることができます。

「距離」は、速さと時間が分かっていれば求めることができます。

例えば、分速50m の速さで 7分歩いたとする。1分で 50m 進む速さで 7分歩く、つまり 1分の 7倍の時間歩くのだから、1分で進む距離の 7倍の距離を進めるということ。

なので、1分で進む距離 50m × 7 で進んだ距離を求めることができますね。

「時間」を求める計算、距離÷速さ、は一番分かりにくいかもしれないですね。

これは「速さ」を、「1分あたり 50m 進む」ではなく「50m 進むのに 1分かかる」と考えると分かりやすいのかもしれません。

350m の距離を分速50m で進む場合、350ｍ の中に 50m がいくつあるかを考える。それが「距離÷速さ」350÷50 で、50ｍ が 7つあるから 350m 進むのに 7分かかるということ。

速さ、距離、時間、に関係とそれぞれの計算の意味もきちんと理解して、公式を覚えてないと計算できない、なんていうことの無いようにしておきましょう。

では、問題を解いていきましょう。まずは情報の整理から。

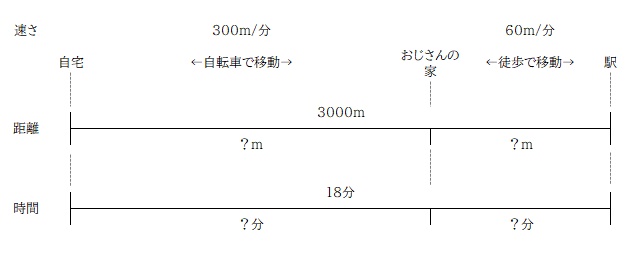
問題で問われているのは「自転車で走った道のり」なので、距離をそれぞれ x , y とおいて式を立てるのが良さそうですね。

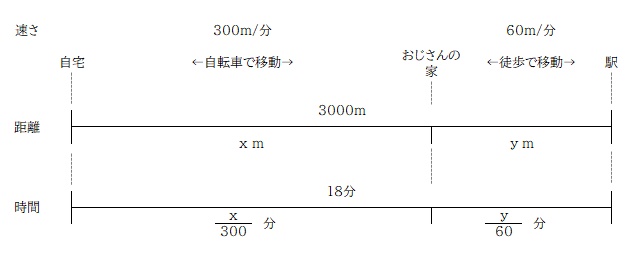
自転車で走った距離を x とすると、自転車で走った時間を 距離÷速さ で表すことができます。歩いた距離を y とし、こちらも同様に時間を y を使って表します。

距離の合計が 3000m、時間の合計が 18分なので、方程式をふたつ立てることができるので、あとは連立方程式で解くだけ。

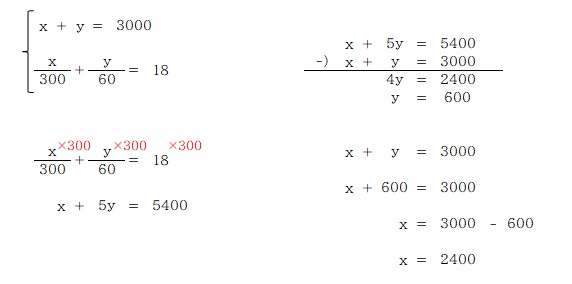
A. 2400m

先の解き方では、距離を x , y とおいて式を立てましたが、時間の方を x , y としても当然解くことができます。

問題の解き方を覚えただけ、ではあまり意味がないので文章問題の指導をするときは子どもたちに大抵の場合こう言います。

「じゃあ次は時間の方を x , y とおいて解いてみて！」と。

ということで別解。

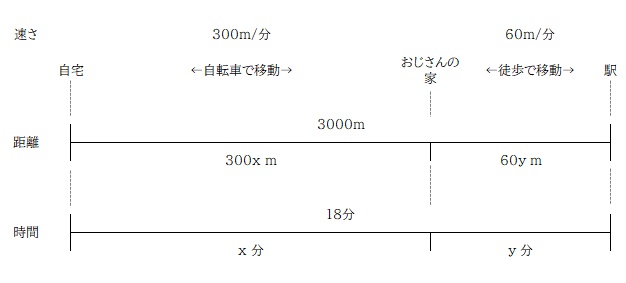
自転車で走った時間を x とすると、自転車で走った距離を 速さ×時間 で表すことができます。歩いた時間を y とし、こちらも同様に距離を y を使って表します。

時間の合計が 18分、距離の合計が 3000m なので、方程式をふたつ立てることができるので、あとは連立方程式で解くだけ。

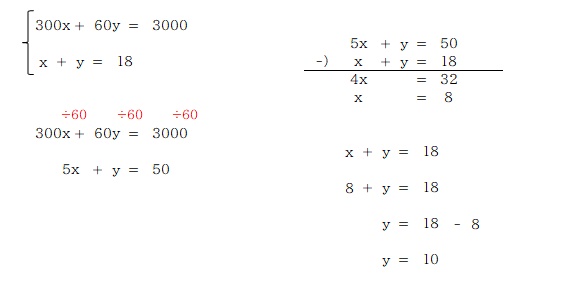
ということで x と y を求めることができましたが、もちろんこれは答えではありません。問われているのは「走った道のり」で、計算で求めた x , y の値は「走った時間」と「歩いた時間」です。

数学の文章問題を「解き方」でしか覚えない子はこういうところで躓きます。式の意味、計算の意味、何を文字において、計算の結果何を求めたのか、をきちんと考えながら問題を解く癖をつけましょう！

計算の結果、「x」、つまり走った時間が 8分だと分かりました。分速 300m で 8分間走ったのだから、走った距離は 300×8 で 2400m が解となります。

また、走った時間を x とした時、走った距離は 300x と表しているのだから、そこに x=8 を代入して、300×8 で 2400m と考えても良いですね。

A. 2400m

問題の解き方を覚える。そういう勉強をしている子は応用が利きません。問題で問う内容を一部だけ、ほんの少し変えるだけで正解できなくなったりします。

例えば、この問題だとちょっと意地悪して「走った道のりは何km ですか？」と少しだけ求める答えの単位を変えるだけで正解できなくなったりします。

理由は「覚えた解き方」のなかに「求めた解の単位を変える」という工程が含まれていないから。

逆に「覚えた解き方」のなかに「求めた解の単位を変える」という工程が含まれていた場合、類題を解くときに、する必要のない「単位を変える計算」をして不正解になるパターンもあったりします。

問題を解く過程、その計算の意味を理解しようとしないと、このように全く応用が利かなくなるということが多々あります。

問題を解くための計算の仕方を覚える勉強ではなく、問題を解くための計算の意味を一つひとつきちんと理解しようとする、そういう勉強をしていって欲しいものですね。

-----

問題を解けば終わり、答えが分かれば終わり、ではなく、問題を解く過程でたくさんの「なんだろう？」っていう疑問を見つけて、それを理解していく努力が勉強です。

そしてその「なんだろう？」を解き明かしたときの達成感を味わうのが勉強の醍醐味です！

ぜひたくさんの「分からない」を見つけて、それを「分かった！」に変えていく努力をしていってくださいね！

以上です。お疲れさまでした！
(*ᴗˬᴗ)⁾⁾