子育て&学力アップの応援ブログ ~数学~
2023年
4月
30日
日
「分からない」を考えよう! #22
生徒たちの「分からない」を取り上げて考えていきます。
解き方が分からない前提で「どんな風に考えて解いていくか」という過程を書いていくので、ぜひご自身でも解き方を考えながら読み進めてみてください。
今回は、中学3年の数学「因数分解」からの出題。塾の教材にあった問題2問、ネットで見つけた問題1問です。新年度最初の中間テストの範囲になるのでしっかり理解して自由自在に扱えるよう勉強しておきましょう!
問題
(1)
x+y=5 , xy=-6 であるとき、( x - y )² の値を求めよ。
(2)
x+y=-4 , xy=3 であるとき、x² + 3xy + y² の値を求めよ。
(3)
a-b=3 , ab=3 であるとき、2a² + 2b² の値を求めよ。
平方完成という考え方を利用して解く問題ですね。
まずは、問題(1) を見ていきましょう。
問題を解くための考え方は、
「( x - y )² の値を求めよ」とあるけど、提示されている値は「x+y=5」となっている。ということは問題の「( x - y )²」が「( x + y )²」だったら値を代入して解けるよね。
となります。
そして、「( x - y )²」を「( x + y )²」に変形させるために平方完成の考え方を使います。
-----
ということで平方完成について説明します。
例えば、「x² + y²」という式があり、これを平方の形、つまり因数分解して「( x + y )²」に変形を完成させるための考え方が平方完成です。
x² + y²
↓
( x + y )²
このように因数分解できるようにしたい。それを考えるために、まずは下の式を展開してみましょう。
x² + y²
↓
x² + 2xy + y²
こうしてみると、和の平方で因数分解するためには「+2xy」が足りないことが分かりますね。ここで必要な考え方はふたつ。
①足りなければ足してあげれば良い
②元の式とイコールの関係を維持するため、勝手に足した式と同じものを引けば良い
つまり①の操作は、
x² + y² ≠ x² + y² + 2xy
右の式になるが、これでは元の式とイコールではなくなってしまうので、
②の操作をして、
x² + y² = x² + y² + 2xy - 2xy
このようにしてあげる。これで「+ 2xy - 2xy」の部分を計算したら元の式「x² + y²」とイコールですよね。この状態で、
x² + y² = ( x² + y² + 2xy ) - 2xy
この部分を因数分解してあげると、
x² + y² = ( x² + 2xy + y² ) - 2xy
x² + y² = ( x + y )² - 2xy
このように、平方プラスα という形に変形させるのが平方完成の考え方です。
では、問題の解説↓
問題(1)
x+y=5 , xy=-6 であるとき、( x - y )² の値を求めよ。

「( x - y )²」の値を求めたい。けど、与えられた値は「x+y=5」となっている。
もし「( x - y )²」が「( x + y )²」だったら「x+y=5」を代入できるのに。
じゃあ「( x - y )²」を「( x + y )²」に変えちゃおう!
ということで、この考え方を実現させるのに使うのが平方完成ですね。具体的な解き方は上記の通りです!
ここまで、なんとなくでも理解できたかな。
しっかり考えて理解できたと思ったら問題(2)(3)は自力で解いてみてください。
解説は↓
問題(2)
x+y=-4 , xy=3 であるとき、x² + 3xy + y² の値を求めよ。

問題(3)
a-b=3 , ab=3 であるとき、2a² + 2b² の値を求めよ。

平方完成についてしっかりと理解し扱えるように勉強してみてください。
ところで、この 問題(1) ですが、生徒が「平方完成を使って解く」ことが出来なかったので取り上げたのですが、この生徒は全く別のアプローチで問題自体は解いています。
私はその考え方をしなかったので凄いなと感心しました。ということで別解。
-----
問題(1)
x+y=5 , xy=-6 であるとき、( x - y )² の値を求めよ。
-----
生徒が目を付けたのは「x+y=5 , xy=-6」このふたつの式。
足して「5」、掛けて「-6」になる x , y の値を考え、
x=(-1) , y=6
を導き出し、( x - y )² に代入して解く。
問題の解き方はひとつじゃないです。ひとつの解き方だけに捉われない柔軟な思考を大切に育てていきたいと思わされました。
ちなみに、この別解のアプローチ。
問題(2) も同様に解くことができますが、問題(3) は厳しいかもしれないですね。少なくとも x, y の値をパッと割り出すことはできそうにないです。
学校の勉強において、基本的に問題の答えは「ひとつ」として用意されているものですが、その答えにたどり着く方法はひとつとは限らないので、自由な発想で解にたどり着くその過程を楽しんでみてくださいね!
以上です。お疲れさまでした!
(*ᴗˬᴗ)⁾⁾
2023年
4月
22日
土
「分からない」を考えよう! #21
生徒たちの「分からない」を取り上げて考えていきます。
解き方が分からない前提で「どんな風に考えて解いていくか」という過程を書いていくので、ぜひご自身でも解き方を考えながら読み進めてみてください。
今回は、中学3年の数学「因数分解」からの出題。高校入試の過去問からですが、少し数字はいじっています。新年度最初の中間テストのテスト範囲になるのでしっかり理解して自由自在に扱えるよう勉強しておきましょう!
問題
次の計算をしなさい。
2023³ - 2023² × 2022 - 2022²
この問題を解こうと思ったら、やり方はふたつあって、
1.力づくで全部計算して解く
2.楽に解ける工夫を考えて解く
なんだけど、こういう問題って基本的には考えて工夫することで楽に解けるように作られています。なので色々工夫して解く努力をしてみましょう。
がんばって考えても「全然分からない」ってなったら解答/解説を見てみましょう。もちろん、それを写して終わりにしちゃだめですよ。それを見たうえで、そこからヒントをつかんで問題を解く糸口にしましょう。
ということで、この問題の解説を見てみます。
-----
与式 = 2023²×(2023-2022)-2022²
-----
はじめの一行だけ見てみると、このように書いてある。私であれば見るのはここだけ。何をどうして、どういう考え方で、式を変形しているのか、「何でこうなるんだろう?」をまずは理解できるように考えます。
たとえば、
①数字の値を「文字」に置き換える。
2023=A , 2022=B とする。
2023³-2023²×2022-2022²
=A³-A²B-B²
このように文字式にすると、式の前半「A³-A²B」を共通因数「A²」で括るのか、っていうことに、気付きやすいのではないかと思います。
ほかにも、
②累乗の表記を全て掛け算に直す。
2023³-2023²×2022-2022²
=(2023×2023×2023)-(2023×2023×2022)-(2022×2022)
このように書いてみても、前半ふたつの式の中に共通因数「2023×2023」があることに気付きやすくなるかもしれないですね。あまりスマートではないですけどね。
問題を解くうえで大切なことは、その過程にある考え方をきちんと理解すること。理解するため、であれば解答/解説を見ながら考えることは全然アリですよ!
それでは私の解答を。↓

なかなか解きごたえのある面白い問題でしたね。
何のために問題を解くのか。宿題や課題が何のために出されるのか。
終わらせることが目的になってしまうと、その努力はただの作業です。
理解することが目的となった努力が「勉強する」ということです。
問題を解く過程の、いろいろな考え方を理解していくことは、その問題だけでなく様々な問題を解くための武器となるので、「分かろう!」っていう勉強を、がんばってくださいね!
以上です。お疲れさまでした!
(*ᴗˬᴗ)⁾⁾
2023年
4月
15日
土
「分からない」を考えよう! #20
生徒たちの「分からない」を取り上げて考えていきます。
解き方が分からない前提で「どんな風に考えて解いていくか」という過程を書いていくので、ぜひご自身でも解き方を考えながら読み進めてみてください。
今回は、中学3年の数学「式の展開」からの出題。いくつかの教材から問題をピックアップしてきました。新年度最初の中間テストのテスト範囲になるのでしっかり理解して自由自在に扱えるよう勉強しておきましょう!
問題
次の式を展開せよ。
(1)
( x + y - 6 ) ( x + y - 8 )
(2)
( x - y + 5 ) ( x - y - 5 )
(3)
( x + 3y - 2 ) ( x + y - 2 )
(4)
( a + b - 3 ) ( a - b - 3 )
(5)
( a + b - 2 ) ( a - b + 2 )
ここで学んでおきたい考え方は、文字の置き換え、です。
もちろん、そんなことをせずに一つひとつ丁寧に計算して解いてもいいんだけど、もっと複雑な問題だとその計算も大変になるかもしれません。
問題を解くうえで色々な考え方を知っていれば、計算がとても楽になるケースもたくさんあるので、ぜひ身に付けておきましょう。
(1) と (2) は基本的な置き換えのパターン。
(3) と (4) は置き換える式がまとまっていないのでちょっとだけ分かりにくいパターン。特に (4) の方は置き換える部分を間違いやすいです。
(5) はそのままでは置き換えができないので符号の操作が必要なパターン。この中では一番難易度が高い問題ですね。
中学3年生は、解説を見る前に自分で解けるかチャレンジしてみてください!
では解説。
↓
問題(1)

置き換えの基本問題その1。x+y=M と置き換えることで、
乗法公式 (x+a)(x+b)=x²+(a+b)x+ab
が利用できる形にりますね。公式の x , a , b の値はそれぞれ M , -6 , -8 となるので、この値で展開。置き換えた M を元に戻します。最後に、
乗法公式・和の平方 (x+a)²=x²+2ax+a²
分配法則 a(b+c)=ab+ac
といった復習も踏まえつつ展開すれば解となります。
問題(2)

置き換えの基本問題その2。x-y=M と置き換えることで、
乗法公式・和と差の積 (x+a)(x-a)=x²-a²
が利用できる形にりますね。公式の x , a の値はそれぞれ M , 5 となるので、この値で展開。置き換えた M を元に戻します。最後に、
乗法公式・差の平方 (x-a)²=x²-2ax+a²
の復習も踏まえつつ展開すれば解となります。
ちょうど (1) (2) を解く過程で乗法公式4つ全部登場するので良い復習になりますね。これらの公式をきちんと扱えないのであればここで勉強しなおしておきましょう。
問題(3)

置き換えに使う共通の値 x , -2 が並びで置いてない、っていうだけ。頭の中できちんと処理できるならそのまま置き換えればいいけれど、自信がないなら一旦並べ替えてから置き換えるのが良いかもしれないですね。
あとは、置き換えて展開、戻して展開、するだけです。
最後に出来上がった多項式の式の並びを整理していますが、これはしてもしなくても大丈夫だと思います。この問題の解答では並べ直していたので、それに倣っています。
並べ方の作法は大まかに、
①次数の大きなものから
②アルファベット順
だけ押さえておけばいいと思います。この問題であれば、
x²=xx , 4xy , 3y²=3yy → 文字2つなので次数は2
-4x , -8y → 文字1つなので次数は1
4 → 文字無しなので次数は0
ということで上のような順に並べています。
個人的にはキレイに並んでいる方が気持ちいいですし、例えば「先生が採点しやすくなれば良いな!」なんて考える優しさがあると素敵だな、って思います。
問題(4)

この問題の間違いやすいポイントは、パッと見て b-3 を置き換えてしまう点。確かにどちらの式にも b-3 が含まれていますが、これは誤り。結構ここ分かっていない子は多いです。
よく見誤るポイントなので気を付けましょう。
この式の値を整理すると、
左側:( a+b-3 ) → a , b , -3
右側:( a-b-3 ) → a , -b , -3
となります。なので b-3 を同じものとしては扱えないということ。共通部分は a-3 となります。あとはこれを別の文字に置き換えて展開、文字を戻して展開すれば解となります。
ちなみのこの問題の解答は展開後の式のままで、特に並べ直しはされていませんでした。そんな感じで「キレイに並べないとダメ」と言ったルールはなく結構アバウトです。並べ直すなら、
a²-b²-6a+9
でしょうか。なのでこの辺りは気楽に考えましょう。
問題(5)

この問題はこのままでは置き換えが使えません。式の値を整理すると、
左側:( a+b-2 ) → a , b , -2
右側:( a-b+2 ) → a , -b , 2
ここで注目する点は b , 2 の符号があべこべになっていること。つまり左側の b , -2 の符号をひっくり返せば -b , 2 となり右側の式と揃えられます。その逆もまた然り。
そこでそのためのテクニックが符号の操作。-1 で括る、という考え方が分かりやすいかな。そうすることで置き換えが使える形に整えることが可能です。
例1: -a+b = -(a-b)
例2: -a-b = -(a+b)
ここさえわかれば、あとは置き換えて展開、戻して展開のいつも通りの処理で解を出せます。
最後に気を付けるポイントは、(b-2)² を展開したときの式を括弧の中に入れておくこと。
-(b-2)² は (-1)×(b-2)² っていう掛け算だから
っていう説明でなんとなく理解できるだろうか。ミスしやすいポイントなので気をつけましょうね。
さて、この問題、ちゃんと理解できたでしょうか?今回の解説では右側の式の -b+2 を括って符号操作したけれど、当然左側の式をいじって解くことも可能です。
ということで、ここまでちゃんと理解できた!と思えたなら、ぜひ左側の式の b-2 の方を符号操作して解くことにチャレンジしてみてください!こんな感じで自分の中の理解を確認することは大切ですよ!
解説は↓
問題(5) 別解

文字に置き換えるときに分かりやすいよう右側の式も整理しています。文字式の計算、符号の扱い、その辺りきちんと理解していれば大丈夫なはず。
よく分からないことが、きちんと分かるようになると楽しいですよね。
勉強がんばって!そして楽しんでください!
最後に。式の置き換えに使用した文字、今回は「M」でしたが、これじゃなきゃダメってことではなくどんな文字を使っても ok です!
問題を見てると「A」や「X」なんかも使ったりしていますが、大文字を使う理由は、式にあるもともとの文字と区別しやすいように、ということだと思います。
小文字の「x」がある問題で置き換えに大文字の「X」を使うと紛らわしいから避けた方がいいかも、とか、いろいろ考えて好きな文字を使って解いてください。
ちなみに、こういった置き換えで「M」をよく使う理由は、
modify 修正する/変更する
の頭文字をとって「M」をよく使う、そういう慣習がある、という感じのようです。
式の展開を置き換えを活用して解く、という本題からはズレた事柄ですが、勉強ってこういう寄り道の方が楽しかったりしますよね。
以上です。お疲れさまでした!
(*ᴗˬᴗ)⁾⁾
2022年
7月
13日
水
「分からない」を考えよう! #19
生徒たちの「分からない」を取り上げて考えていきます。
解き方が分からない前提で「どんな風に考えて解いていくか」という過程を書いていくので、ぜひご自身でも解き方を考えながら読み進めてみてください。
今回は、とある中学の「2年 1学期 期末テスト」で出題された、数学 (連立方程式) の問題です。
問題

この学校の期末テスト (2年 数学) の問題の中では、これが一番難しかったんじゃないかな、と思います。式を立てて連立方程式で解いて x , y を求める、といったシンプルな構成の問題ではないですね。
けど、やってみると意外と簡単に解けてしまいます。
-----
まずは情報の整理から。
①「n」は 3ケタの自然数、一の位は 8 である。
②「n」は "百の位の数" と "十の位の数" と "一の位の数" の和の 28倍と等しい。
この条件を満たす「n」を求めればいいわけですね。また、わざわざ問題文に「すべて」と記載し下線で強調していることから「n」は複数ある可能性が高いです。
ということで、上記 2点から数式を書いていきます。
自然数「n」の 3ケタの数字のうち "百の位の数" と "十の位の数"が分からないので、
百の位の数 → x とする
十の位の数 → y とする
①「n」は 3ケタの自然数、一の位は 8 である。
n = 100x + 10y + 8 ・・・ ①
②「n」は "百の位の数" と "十の位の数" と "一の位の数" の和の 28倍と等しい。
n = (x + y + 8) × 28 ・・・ ②
このように、問題文の記述から 2つの方程式を書くことができる。この時点でそれぞれの方程式に含まれる文字は 3つずつあるので、このままでは解くことはできません。けれど、どちらも「n」を表した式なので①の右辺を②の左辺に代入し一つにまとめることにします。
100x + 10y + 8 = (x + y + 8) × 28 ・・・ ③
これで式に含まれる文字を一つ減らすことができました。それでもこの式を解いて x , y を求めることはできません。
けれどもし x , y のうちどちらかの値が決まってしまえば、残りの文字の値も求めることができますね。だったら決めてしまえばいい、というのがこの問題を解くカギになります。
x と y に当てはまる可能性のある数字について考えます。
それぞれ 3ケタの整数の "百の位の数" と "十の位の数"を表している、ということは当てはまる可能性があるのはどちらも「ひとケタの整数」ということになります。
また、"百の位の数"の方には「0」は当てはまらない (たとえば「018」だと 2ケタの自然数になってしまうから) ということも分かります。
つまり、
x = 1,2,3,4,5,6,7,8,9
y = 0,1,2,3,4,5,6,7,8,9
それぞれの解はこれらの数字だけに絞ることができる、ということ。
あとは式③に順に代入し条件に当てはまる組み合わせを探れば解くことができそうです。たとえば、x=1 のときの y の値を求める、x=2 のときの y の値を求める、といった感じです。
そこでまずは式③を整理します。
100x + 10y + 8 = (x + y + 8) × 28
100x + 10y + 8 = 28x + 28y + 224
50x + 5y + 4 = 14x + 14y + 112
50x - 14x + 4 -112 = 14y - 5y
36x - 108 = 9y
4x - 12 = y
y = 4 ( x - 3 ) ・・・ ③´
この式に x の値を代入し、条件に合う組み合わせを考えます。
まず ( x - 3 ) ですが、この計算がマイナスになる x の値は NG になります。理由は y の値がマイナスになるから。
ということで x = 1,2 は除外。考えるのは x = 3 からで良さそうです。ということで計算していくと、
x = 3 のとき y = 0
x = 4 のとき y = 4
x = 5 のとき y = 8
これ以降は y の値が 2ケタとなり条件に合わなくなるため、文字の値として適当なのはこの 3通りだけということになります。
よって求める解、3ケタの自然数 n は、
A. n = 308, 448, 588
いかがでしたでしょうか。一見、解き方も分からない難しそうな問題かもしれませんが、一つひとつ順に考えていけば意外と簡単に解くことができます。
問題を見て「難しい」「分からない」と思ったとしても、とりあえず分かるところからやってみる、とりあえず問題文から式を考え立ててみる。頭の中で考えるだけではなく、まずはできることから、とりあえずペンを持ちノートを広げて手を動かす!
こういう問題を自分で考えて解くことができるようになってくると、きっと数学が面白く感じるようになるんじゃないかな。ぜひ、チャレンジしてみれください!
-----
問題を解けば終わり、答えが分かれば終わり、ではなく、問題を解く過程でたくさんの「なんだろう?」っていう疑問を見つけて、それを理解していく努力が勉強です。
そしてその「なんだろう?」を解き明かしたときの達成感を味わうのが勉強の醍醐味です!
ぜひたくさんの「分からない」を見つけて、それを「分かった!」に変えていく努力をしていってくださいね!
以上です。お疲れさまでした!
(*ᴗˬᴗ)⁾⁾
2022年
7月
12日
火
「分からない」を考えよう! #18
生徒たちの「分からない」を取り上げて考えていきます。
解き方が分からない前提で「どんな風に考えて解いていくか」という過程を書いていくので、ぜひご自身でも解き方を考えながら読み進めてみてください。
今回は、とある中学の「2年 1学期 期末テスト」で出題された、数学 (連立方程式) の問題です。
問題

これもそんなに難しい問題ではないですね。それでも、数学を「解き方」でしか考えられない場合、当然「解き方」を知らなければ解けない、どうすればいいか分からない、となってしまいます。
数学の文章問題は「解き方」なんて知らなくても「文章を読んで、情報を整理し、考える」ことさえできれば解くことができるので、仮にこの問題の「解き方」を知っていたとしても、それは一旦横に置いておいて、自分で考えて解いてみてくださいね。
-----
ではまず、問題文で提示されている情報を整理してみましょう。
・100円玉が何枚かある。枚数は不明。金額は 枚数×100 で表すことができる。
・500円玉も何枚かある。枚数は不明。金額は 枚数×500 で表すことができる。
・これら全部合わせると 4800円になる。
そのお金を両替した。
・100円 1枚 → 50円 2枚に、つまり枚数は 2倍になる。
・500円 1枚 → 100円 5枚に、つまり枚数は 5倍になる。
・両替後の 100円玉の枚数は、両替後の 50円玉の枚数より、9枚多い。
言い換えると「100円玉の枚数」引く「50円玉の枚数」が「9枚」ということ。
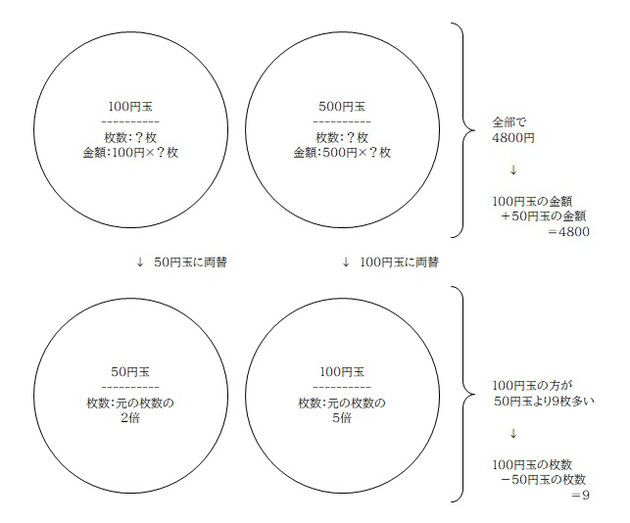
こんな感じでしょうか。これを数式にするために分からない値を記号に置いて考えます。問題の (1) で「x枚の 100円玉」と記述があるので、
元の 100円玉の枚数:x枚
元の 500円玉の枚数:y枚
とし、整理します。
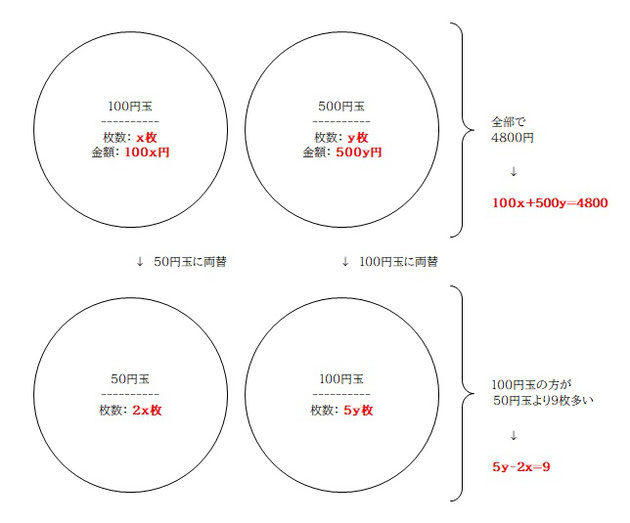
ここまで整理すればあとはただの計算問題ですね。
-----
(1)
この問題の肝は両替後の枚数をきちんと数式で表すことができるかどうか。わざわざ小問でそこの確認をさせてくれています。
問題文を読んで情報の整理をしっかりとしていればすでに答えは出ていますね。
A. (1) 2x
-----
(2)
この問題も、すでに方程式ふたつ完成しているのであとは解くだけ。
元の 100円玉の枚数:x枚
元の 500円玉の枚数:y枚
としているので x , y の値を求めればそれがそのまま答えですね。
100x+500y=4800 ・・・ ①
5y-2x=9 ・・・ ②
解き方は色々、どう解くのも自由ですが、なるべく大きい数字は扱わないほうが楽なので、まずは①の式を 100 で割って、
x+5y=48
これを 2倍します。
2x+10y=96 ・・・ ①´
②の式は x と y の項の並びが逆なので、これも整理して、
-2x+5y=9 ・・・ ②´
x の項がプラスとマイナスなので①´と②´を足して連立方程式を解きます。
2x+10y=96
-2x+5y=9
15y=105
y=7
これを①´に代入。
2x+70=96
2x=26
x=13
A. (2) 100円玉:13枚、500円玉:7枚
そういえば文章問題って答えが正しいかどうか、確認することもできます。求めた答えで問題文の通りになるかを確認するだけ。
100円玉 13枚 → 1300円、500円玉 7枚 → 3500円
金額を合計すると 4800円
100円玉 13枚を 50円玉に両替 → 26枚、500円玉 7枚を 100円玉に両替 → 35枚、
35-29=9 で、両替後の 100円玉の方が 9枚多い
すべて問題文の条件を満たしていますね。
求めた解に自信がなければ、こうやって確認するといいですよ!
-----
問題を解けば終わり、答えが分かれば終わり、ではなく、問題を解く過程でたくさんの「なんだろう?」っていう疑問を見つけて、それを理解していく努力が勉強です。
そしてその「なんだろう?」を解き明かしたときの達成感を味わうのが勉強の醍醐味です!
ぜひたくさんの「分からない」を見つけて、それを「分かった!」に変えていく努力をしていってくださいね!
以上です。お疲れさまでした!
(*ᴗˬᴗ)⁾⁾
2022年
7月
11日
月
「分からない」を考えよう! #17
生徒たちの「分からない」を取り上げて考えていきます。
解き方が分からない前提で「どんな風に考えて解いていくか」という過程を書いていくので、ぜひご自身でも解き方を考えながら読み進めてみてください。
今回は、とある中学の「2年 1学期 期末テスト」で出題された、数学 (連立方程式) の問題です。
問題

この問題は、「2つの連立方程式の解は同じ」、これの意味をきちんと理解できるかどうか、がポイントかな。そこさえ分かれば、あとは、
1. 連立方程式を解き x , y を求める。
2. x , y を代入、方程式を解き a を求める。
3. x , y を代入、方程式を解き b を求める。
これだけなので簡単ですね。では解いていきます。
まずは「2つの連立方程式の解は同じ」ということについて。解が同じになるということは、4つの方程式のうち、連立方程式をどの組み合わせで解いても x , y の値が同じになるということ。
連立方程式の勉強をしている時点では、次の単元である一次関数は当然習っていないのだけれど、「2つの連立方程式の解は同じ」ということがどういうことかを簡単に理解するために一次関数のグラフで考えてみます。
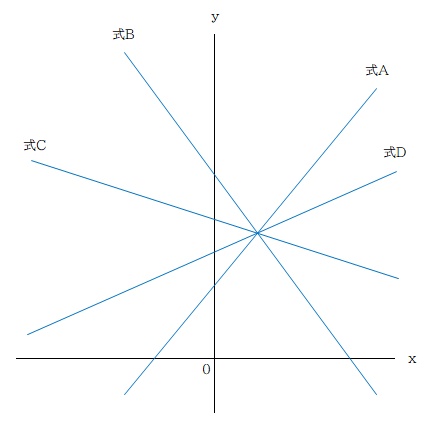
グラフにするとこんなイメージかな。
すべての解は同じ → x , y が同じ → すべての式 (直線) の交点が同じ
っていう感じ。どの式の組み合わせで連立方程式を解いても良いということになります。
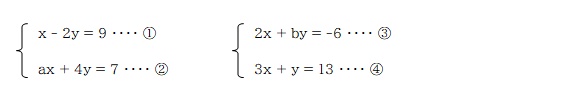
ひとつの方程式のなかに文字 (分からない値) が3つ含まれている式②③は使えないので、式①④を連立方程式で解けば良い、ということですね。
ここさえ理解できればあとはただの計算問題です。
x - 2y = 9 ・・・ ①
3x + y = 13 ・・・ ④
①を 3倍して、
3x - 6y = 27 ・・・ ①´
①´から④を引く
3x - 6y = 27
3x + y = 13
-7y = 14
y = -2
y の値を①に代入
x - 2y = 9
x + 4 = 9
x = 5
x=5 , y=-2 を式②③に代入し a , b を求める
ax + 4y = 7
5a - 8 = 7
5a = 15
a = 3
2x + by = -6
10 - 2b = -6
-2b = -16
b = 8
A. a=3 , b=8
この問題は、最初に式①②と式③④がセットで提示されているので、「解が同じ」の意味をちゃんと考えられないと、「式②③で連立方程式で解けばいいんだ!」という発想に至らないのかもしれないですね。
一次方程式も連立方程式も、他のどんな単元の文章問題もすべて同じですが、問題を解くために必要な情報は全て問題文の中に用意されています。
大切なのは与えられた情報をちゃんと読み解くこと。
ちなみに勉強ができない子は「問題文を読んで考える」のではなく「問題文を見て解き方を知ってる問題かどうかを判断している」だけのことが多い。
なので、そういう子の「先生、この問題分かりません」という質問は「先生、この問題の解き方を知りません」ということが大半です。
文章問題を解けるようになりたいなら、まずは問題文をちゃんと読んで考えること!
勉強頑張ってくださいね!
----
問題を解けば終わり、答えが分かれば終わり、ではなく、問題を解く過程でたくさんの「なんだろう?」っていう疑問を見つけて、それを理解していく努力が勉強です。
そしてその「なんだろう?」を解き明かしたときの達成感を味わうのが勉強の醍醐味です!
ぜひたくさんの「分からない」を見つけて、それを「分かった!」に変えていく努力をしていってください。
以上です。お疲れさまでした!
(*ᴗˬᴗ)⁾⁾
2022年
7月
08日
金
「分からない」を考えよう! #16
生徒たちの「分からない」を取り上げて考えていきます。
解き方が分からない前提で「どんな風に考えて解いていくか」という過程を書いていくので、ぜひご自身でも解き方を考えながら読み進めてみてください。
今回は、とある中学の「2年 1学期 期末テスト」で出題された、数学 (式の計算) の問題です。
問題

文章から式を立てて解くのではなく、式を立てて等式変形する問題。解き方を覚える勉強をしている子は、こういう変化球に弱いです。
早速解いていきましょう。まずは情報の整理。
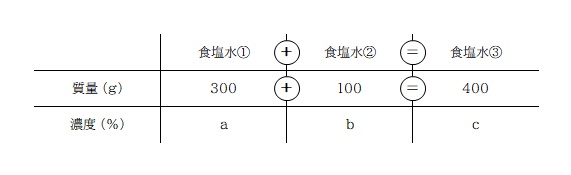
食塩水の質量は足して式にすることができるけど、濃度の方はそのまま足せるものではないですね。なので、食塩水の質量と濃度から、食塩水に含まれる食塩の質量を文字式で表しましょう。それであれば足して方程式にすることが可能です。
濃度の計算は、例えば食塩水① の場合、300g を 100個 とした時の a個分が食塩の量になります。なので、300g の a/100 で表すことができますね。
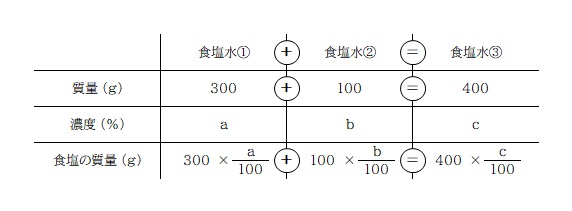
あとは、食塩の質量で作った方程式を整理し c= の形にするだけ。
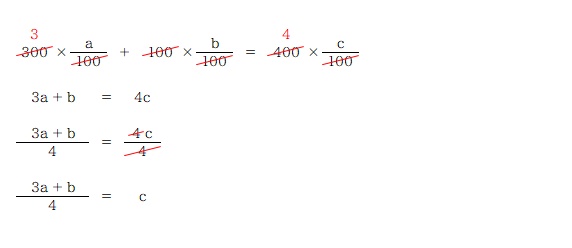

特に難しい問題というわけではないですが、普通に式を解いて質量やら濃度を求める問題の解き方を覚える勉強をしていると、こういう風に少し捻った出題をするだけで「分からない!」ってなって思考停止してしまいます。
文章問題は「覚えた解き方通りに解く」のではなく、「問題文を読んで考えて解く」よう意識して勉強してください。
-----
問題を解けば終わり、答えが分かれば終わり、ではなく、問題を解く過程でたくさんの「なんだろう?」っていう疑問を見つけて、それを理解していく努力が勉強です。
そしてその「なんだろう?」を解き明かしたときの達成感を味わうのが勉強の醍醐味です!
ぜひたくさんの「分からない」を見つけて、それを「分かった!」に変えていく努力をしていってくださいね!
以上です。お疲れさまでした!
(*ᴗˬᴗ)⁾⁾
2022年
7月
07日
木
「分からない」を考えよう! #15
生徒たちの「分からない」を取り上げて考えていきます。
解き方が分からない前提で「どんな風に考えて解いていくか」という過程を書いていくので、ぜひご自身でも解き方を考えながら読み進めてみてください。
今回は、とある中学の「2年 1学期 期末テスト」で出題された、数学 (連立方程式) の問題です。
問題

「速さ」の計算は苦手な子が多いイメージですが、いろんな単元の文章問題に登場してくるので、分からなかったり不正解になったときにきっちり見直しをして理解しておくようにしましょう。
数学だけでなく理科でも速さの計算はたびたび登場するので、きちんと理解しておくと様々な場面で勉強が楽になると思いますよ。
-----
ということで、まずは問題を解く前に速さの計算について。
中学生なら「みはじ」などで公式を覚えるのではなく、それぞれの計算の意味を理解しておきましょう。
「速さ」は、単位時間あたりに進む距離を表しています。
つまり、1分あたり何メートル進む、だとか、1時間あたり何キロメートル進む、といった感じですね。
例えば、350m 進むのに 7分かかった場合、350 を 7 で割れば 1分あたり何メートル進むのかを求めることができます。

「距離」は、速さと時間が分かっていれば求めることができます。
例えば、分速50m の速さで 7分歩いたとする。1分で 50m 進む速さで 7分歩く、つまり 1分の 7倍の時間歩くのだから、1分で進む距離の 7倍の距離を進めるということ。
なので、1分で進む距離 50m × 7 で進んだ距離を求めることができますね。

「時間」を求める計算、距離÷速さ、は一番分かりにくいかもしれないですね。
これは「速さ」を、「1分あたり 50m 進む」ではなく「50m 進むのに 1分かかる」と考えると分かりやすいのかもしれません。
350m の距離を分速50m で進む場合、350m の中に 50m がいくつあるかを考える。それが「距離÷速さ」350÷50 で、50m が 7つあるから 350m 進むのに 7分かかるということ。

速さ、距離、時間、に関係とそれぞれの計算の意味もきちんと理解して、公式を覚えてないと計算できない、なんていうことの無いようにしておきましょう。
では、問題を解いていきましょう。まずは情報の整理から。
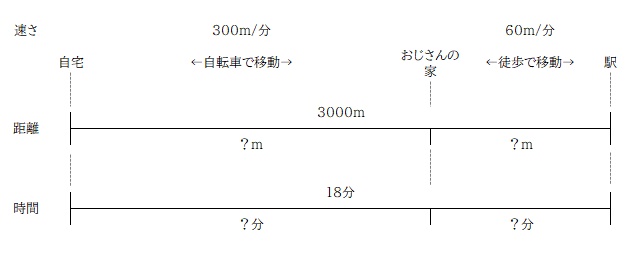
問題で問われているのは「自転車で走った道のり」なので、距離をそれぞれ x , y とおいて式を立てるのが良さそうですね。
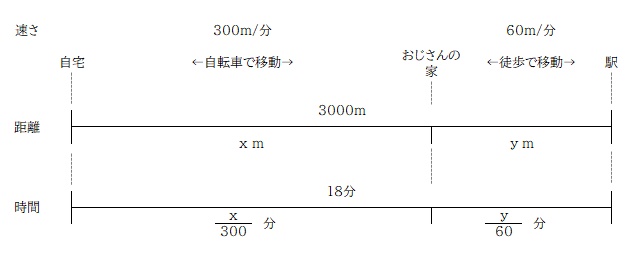
自転車で走った距離を x とすると、自転車で走った時間を 距離÷速さ で表すことができます。歩いた距離を y とし、こちらも同様に時間を y を使って表します。
距離の合計が 3000m、時間の合計が 18分なので、方程式をふたつ立てることができるので、あとは連立方程式で解くだけ。
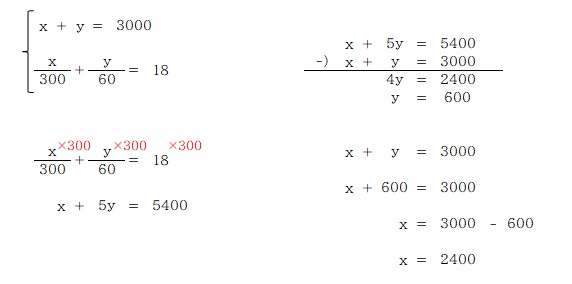
A. 2400m
先の解き方では、距離を x , y とおいて式を立てましたが、時間の方を x , y としても当然解くことができます。
問題の解き方を覚えただけ、ではあまり意味がないので文章問題の指導をするときは子どもたちに大抵の場合こう言います。
「じゃあ次は時間の方を x , y とおいて解いてみて!」と。
ということで別解。
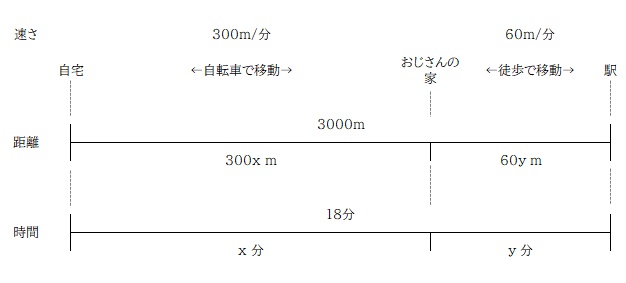
自転車で走った時間を x とすると、自転車で走った距離を 速さ×時間 で表すことができます。歩いた時間を y とし、こちらも同様に距離を y を使って表します。
時間の合計が 18分、距離の合計が 3000m なので、方程式をふたつ立てることができるので、あとは連立方程式で解くだけ。
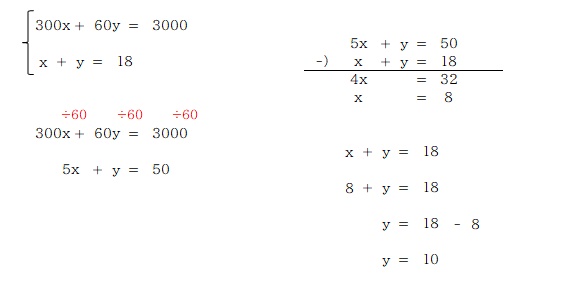
ということで x と y を求めることができましたが、もちろんこれは答えではありません。問われているのは「走った道のり」で、計算で求めた x , y の値は「走った時間」と「歩いた時間」です。
数学の文章問題を「解き方」でしか覚えない子はこういうところで躓きます。式の意味、計算の意味、何を文字において、計算の結果何を求めたのか、をきちんと考えながら問題を解く癖をつけましょう!
計算の結果、「x」、つまり走った時間が 8分だと分かりました。分速 300m で 8分間走ったのだから、走った距離は 300×8 で 2400m が解となります。
また、走った時間を x とした時、走った距離は 300x と表しているのだから、そこに x=8 を代入して、300×8 で 2400m と考えても良いですね。
A. 2400m
問題の解き方を覚える。そういう勉強をしている子は応用が利きません。問題で問う内容を一部だけ、ほんの少し変えるだけで正解できなくなったりします。
例えば、この問題だとちょっと意地悪して「走った道のりは何km ですか?」と少しだけ求める答えの単位を変えるだけで正解できなくなったりします。
理由は「覚えた解き方」のなかに「求めた解の単位を変える」という工程が含まれていないから。
逆に「覚えた解き方」のなかに「求めた解の単位を変える」という工程が含まれていた場合、類題を解くときに、する必要のない「単位を変える計算」をして不正解になるパターンもあったりします。
問題を解く過程、その計算の意味を理解しようとしないと、このように全く応用が利かなくなるということが多々あります。
問題を解くための計算の仕方を覚える勉強ではなく、問題を解くための計算の意味を一つひとつきちんと理解しようとする、そういう勉強をしていって欲しいものですね。
-----
問題を解けば終わり、答えが分かれば終わり、ではなく、問題を解く過程でたくさんの「なんだろう?」っていう疑問を見つけて、それを理解していく努力が勉強です。
そしてその「なんだろう?」を解き明かしたときの達成感を味わうのが勉強の醍醐味です!
ぜひたくさんの「分からない」を見つけて、それを「分かった!」に変えていく努力をしていってくださいね!
以上です。お疲れさまでした!
(*ᴗˬᴗ)⁾⁾
2022年
7月
06日
水
「分からない」を考えよう! #14
生徒たちの「分からない」を取り上げて考えていきます。
解き方が分からない前提で「どんな風に考えて解いていくか」という過程を書いていくので、ぜひご自身でも解き方を考えながら読み進めてみてください。
今回は、とある中学の「2年 1学期 期末テスト」で出題された、数学(式の計算) の問題です。
問題
次の計算をしなさい。

これだけ?そうです。たったこれだけの基本的な計算問題です。
けれど、子どもたちがよく間違えるポイントがふたつもあるので、その点も踏まえてみていきたいと思います。
-----
◆間違いやすいポイント、その1:方程式の計算と混同している。

このように、12 をかけて分数の分母を処理しようとして間違うパターン。これは方程式の勉強をしてきた中学2年生の子がよくやる間違い。
方程式の場合は「両辺に同じ数をかける」から左辺と右辺のイコールの関係が崩れず成り立つのであって、文字式の場合はこのまま計算しただけでは正解することはできないです。

式に 12 をかける、ということは、イコールの向こう側にある「この計算の解」も 12倍されることになるからですね。そのことをきちんと理解していればこの方法で解くことも可能です。それは後ほど。
-----
◆間違いやすいポイント、その2:符号ミス。

マイナスの分数で分子が多項式になっているとき、その多項式中の + や - の符号ミスが多いです。これは文字式でも方程式でも同じ。
計算の仕方をきちんと理解していないと本当によく間違うポイントのひとつですね。
では、解いていきます。
この計算式は方程式ではないので、基本の解き方としては通分して分母を揃え計算を進めていきます。
通分した後、x の項と y の項をそれぞれ計算するため、
「12 分の 2x-8y」を
「12 分の 2x」と「12 分の 8y」に分けるときの符号に注意です。
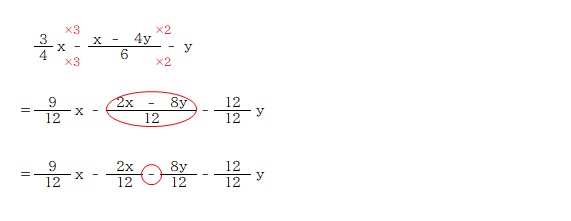
このように「マイナス」にしてしまうのは不正解です。
この計算は「2x から 8y を引いたものを前の数から引いている」のであって、「2x と 8y 両方を前の数から引いている」のではないからですね。
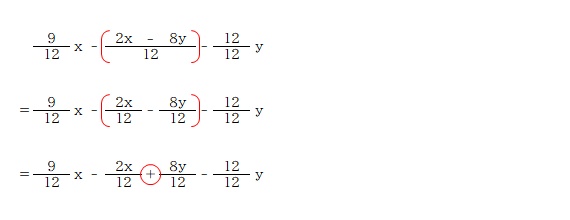
このように括弧を書いて計算すると間違いにくくなると思います。
あとは普通に計算するだけ。

次は、方程式のように分母を処理する方法での計算について。

この計算方法でも同じようにこの部分で符号ミスが多いです。なので先ほどの通武運の計算のとき同様、括弧を付けて考えると間違いにくくなります。
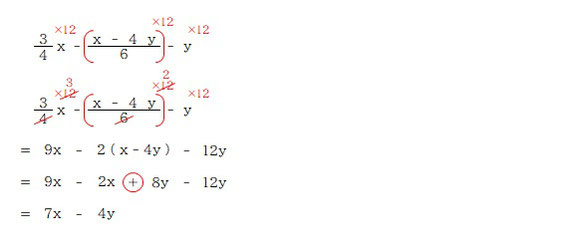
このように符号は + が正解。間違えないように気を付けましょう。
そして最後に、この計算方法は式を 12倍しています。ということは、そこから求められた答えも 12倍されているということ。
つまりここでの解「7x-4y」は本来の答えを 12倍したもの、ということになります。
言い換えると「7x-4y」を 12分の 1 にすれば本来の解になるということ。

一つひとつの計算の意味をきちんと理解していれば、どちらの解き方でも問題なく解くことができます。
しっかり理解して自由自在に扱えるように勉強頑張ってください!
問題を解けば終わり、答えが分かれば終わり、ではなく、問題を解く過程でたくさんの「なんだろう?」っていう疑問を見つけて、それを理解していく努力が勉強です。
そしてその「なんだろう?」を解き明かしたときの達成感を味わうのが勉強の醍醐味です!
ぜひたくさんの「分からない」を見つけて、それを「分かった!」に変えていく努力をしていってくださいね!
以上です。お疲れさまでした!
(*ᴗˬᴗ)⁾⁾
2022年
6月
19日
日
「分からない」を考えよう! #10
生徒たちの「分からない」を取り上げて考えていきます。
解き方が分からない前提で「どんな風に考えて解いていくか」という過程を書いていくので、ぜひご自身でも解き方を考えながら読み進めてみてください。
今回は、塾にあるワークからの出題、数学(2年 連立方程式) の問題です。
問題

今回は、昨日の記事(「分からない」を考えよう! #9)で解いた問題と同じ、割合の計算を含む連立方程式の文章問題です。
なので、昨日の記事を読んでしっかりと勉強をした子なら簡単に解ける問題!
そのはず、なんだけど。
解くことはできる、なのに、正解できない。
そんなトラップが仕掛けられた問題です。ホントはトラップなんていう大層なものではないのだけれど、「昨日の問題を解いている」ということで引っかかる子、気づけない子は多いです。
正解を出せるかどうか、ぜひチャレンジしてみてください。
Let's think!
問題文から分かっていること。
・去年の生徒数は、男女合わせて 480人
・今年は、去年と比べて、
- 男子が 10%減った
- 女子が 4%増えた
- 全体で 13人減った
これを昨日と同じように表に書き込みます。

去年の男子と女子の数が分からないので x , y として考えます。

男子は去年 x人いて、今年はそこから 10%減った、
つまり去年を 100%としたとき今年は 90%になった。なので 0.9 を掛ければいい。
女子は去年 y人いて、今年はそこから 4%増えた、
つまり去年を 100%としたとき今年は 106%になった。なので 1.06 を掛ければいい。
合計は去年の人数から減った分を引けばいいですね。

男子と女子の和が合計なので、

これで2つ式ができたので、あとは連立方程式で解けばいいですね。
-----
②の式に 100を掛けて小数をなくす。

①の式に 90を掛けて、x の項を②´の式と揃える。
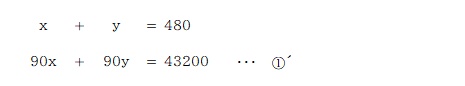
②´の式から①´の式を引いて y を求める。
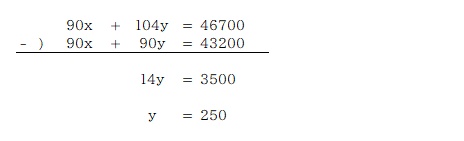
①の式に y の値を代入、x を求める。

ということで、
男子の人数 230人、女子の人数 250人
なのですが!
これが答えだと思った子は残念ながら不正解です。
なぜでしょう。たてた式は正しいです。計算も間違っていません。x と y の値も間違っていません。けど正解ではありません。
なんでなのか?考えてみてください。
Let's think!
なんで正解にならないのか、分かりましたか?
不正解を言い渡し見直しをさせると、生徒は必ずノートを見直します。式が間違っていないか、計算が間違っていないか、けどどちらも間違っていません。
なかなか不正解になった理由に気付けません。
それもそのはず。見直すべきは式や計算といった問題を解く過程ではないからですね。そもそもの前提が間違っています。
なので見直すべきは「問題文」です。
よく読んでみましょう。最後の一文です。
「今年の男子、女子それぞれの生徒数を求めよ。」
求めるのは去年の人数ではなく、今年の人数なんですね。なのでこの解き方で x , y を求めるだけだと不正解になってしまうのです。
とても簡単なことですが、この手の問題を解いたことがあって、表面的な問題の解き方だけを覚える勉強に慣れてしまっている子、なんかはホントによく引っ掛かります。

ということで、この問題の解を求めるには連立方程式で解いた x , y の値を、今年の人数である、男子:0.9x と、女子:1.04y に代入して解としないといけないというわけ。
今年の男子の人数:
0.9x = 0.9×230 = 207人
今年の女子の人数:
1.04y = 1.04×250 = 260人
A. 今年の男子:207人、女子:260人
となります。
-----
ちなみに連立方程式の解がそのまま正解にならないのは、「去年の人数を x , y 」としているからです。
なので「今年の人数を x , y」として解けば、その解がそのままこたえになりますね。
せっかくなので考えてみてください。
難しいポイントは、10%減った/4%増えた、というのが「去年の人数」の対する割合だということ。そこの計算をどうするかですね。
ヒントは税込みの値段を、税込み前の元の値段に戻す計算、を考えればいいですね。
Let's think!
今年の人数を x , y としたとき、去年の人数を x , y を使った数式で表さないといけません。
よくある間違いで、
去年→今年:10%減った、今年→去年:10%増やせばいい
去年→今年:4%増えた、今年→去年:4%減らせばいい
と考えてしまう子もいたりしますが、
10%減った/4%増えた、というのはあくまで「去年の人数」の対する割合なので、これでは不正解。
考え方は、
男子の人数は、去年を 100% としたとき、今年は 90% なのだから、
今年を 90% と考え、それを 100% に戻せば去年の人数になる。
女子の人数は、去年を 100% としたとき、今年は 104% なのだから、
今年を 104% と考え、それを 100% に戻せば去年の人数になる。
という感じ。
もっとシンプルに考えるなら、
たとえば、5倍した数を元の数に戻したいなら?
→5 で割ればいいよね。
というだけの話。
つまり、
男子、去年の人数に 0.9 を掛けたのが今年の人数、ということは
→今年の人数を 0.9 で割れば去年の人数になる。
女子、去年の人数に 1.04 を掛けたのが今年の人数、ということは
→今年の人数を 1.04 で割れば去年の人数になる。

なので、式にするとこんな感じ。割合の考え方、その計算、しっかりと理解して使いこなせるようにしておきましょうね。
あとは、計算していくだけ。
ただ計算は、去年を x , y としたときよりも少しめんどくさくなります。
-----
まずは③の式を連立方程式で解きやすい形に変形していきます。

④の式に 90を掛けて、x の項を③´の式と揃える。
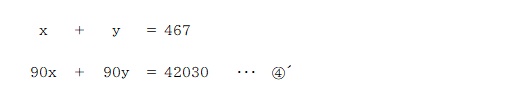
③´の式から④´の式を引いて y を求める。
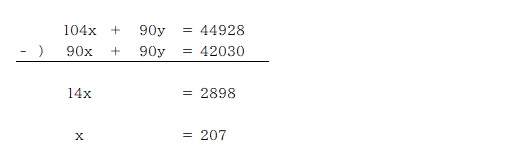
④の式に y の値を代入、x を求める。

先ほどの正解と同じ解を得ることができましたね。
問題の解き方はひとつではありません。
問題を解けば終わり、答えが分かれば終わり、ではなく、問題を解く過程でたくさんの「なんだろう?」っていう疑問を見つけて、それを理解していく努力が勉強です。
そしてその「なんだろう?」を解き明かしたときの達成感を味わうのが勉強の醍醐味です!
ぜひたくさんの「分からない」を見つけて、それを「分かった!」に変えていく努力をしていってくださいね!
以上です。お疲れさまでした!
(*ᴗˬᴗ)⁾⁾
2022年
6月
18日
土
「分からない」を考えよう! #9
生徒たちの「分からない」を取り上げて考えていきます。
解き方が分からない前提で「どんな風に考えて解いていくか」という過程を書いていくので、ぜひご自身でも解き方を考えながら読み進めてみてください。
今回は、とある中学のワークからの出題、数学(2年 連立方程式) の問題です。
問題

連立方程式の文章問題。特別難しいというわけではありませんが、割合の計算、その考え方をきちんと理解していないと解けません。
この記事の投稿時はちょうど1学期の期末テスト前なので、2年生はしっかり勉強してテストに備えておきましょう!
あと、この問題は連立方程式の問題として出題されていますが、一次方程式でも解くことができます。なので1年生もぜひチャレンジしてみてください。
Let's think!
解ける子はすぐ解けたと思います。
分からない!って子は一緒に考えていきましょう。
文章問題を解くコツは、提示された情報をきちんと整理して考えること。
整理すべき情報はまず3つ。
「男子の数」「女子の数」「全体の数」
これら3つの情報をさらに、
「昨年度」「今年度」
の2つの軸でそれぞれ考える必要がありますね。
私が教えるときは次のように書いて考えさせます。

こういう感じの簡単な表に、問題文に書かれている情報、何を x や y といった文字に置き換えるか、を書き込みながら整理していきましょう。
Let's think!
問題文から分かっていること。
・昨年度の生徒数は、男女合わせて 650人
・今年度は、昨年度と比べて、
- 男子が 4%減った
- 女子が 6%増えた
- 全体で 4人増えた
これを表に書き込みます。

このように整理することができます。
なので昨年度の男子と女子の数を文字に置き換えて考えるのが良さそうですね。
昨年度の男子の数を「x」、女子の数を「y」としましょう。

では次に今年度のところを考えていきます。
合計は 650人から 4人増えた、ということなので 654人ですね。
問題は男子の数と女子の数。
ここを文字を使った数式に置き換えましょう。
Let's think!
ここから少し「問題を解く」という本筋から逸れますが、「問題を解く」ために必要な考え方を学ぶために寄り道しましょう。
割合の計算について。
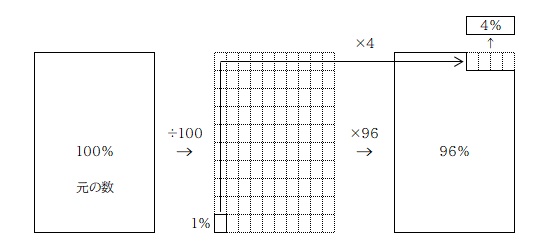
これが問題文にある「4%減った」の考え方。
「4%減る」ということは「96%になった」と言い換えることができるので、「100 を 96 にする」という考え方がひとつ。
計算の仕方は次の通り。

もうひとつは「100 の中の 4 を求めて、元の数から引く」という考え方。
計算の仕方は次の通り。

二通りの考え方、その違いは、
前者は、百分率の状態で 100% から 4% を引いて考えていて、
後者は、元の数の 4% の数を求めて実際の数を引いている、
つまり 4% を減らす計算を「百分率の状態でする」か「実際の数でする」かという違いですね。考え方としては両方理解しつつ、計算については前者の方法を身につけましょう。そのほうが簡単だし扱いやすいです。
ここまでの説明の「元の数」を「1200円」として例を挙げておきます。
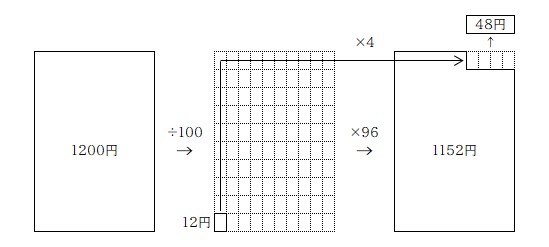
1200円の 4%: 1200×0.04=48円
1200円の 4%減(96%): 1200×0.96=1152円
スーパーでよく見る「20%OFF」とか「4割引き(40%引き)」なんかも同じように計算できますので、いろいろ試してみてください。
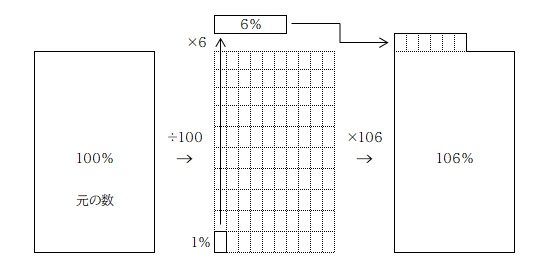
今度は問題文にある「6%増えた」の考え方。
「6%増える」ということは「106%になった」と言い換えることができるので、「100 を 106 にする」という考え方がひとつ。
計算の仕方は次の通り。
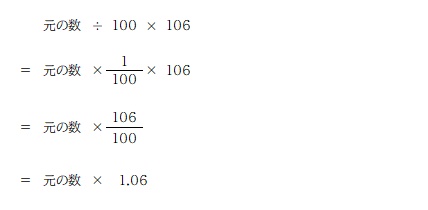
もうひとつは「100 の中の 6 を求めて、元の数に足す」という考え方。
計算の仕方は次の通り。

二通りの考え方、その違いは、
前者は、百分率の状態で 100% に 6% を足して考えていて、
後者は、元の数の 6% の数を求めて実際の数を足している、
つまり 6% を増やす計算を「百分率の状態でする」か「実際の数でする」かという違いですね。考え方としては両方理解しつつ、計算については前者の方法を身につけましょう。そのほうが簡単だし扱いやすいです。
ここまでの説明の「元の数」を「1200円」として例を挙げておきます。
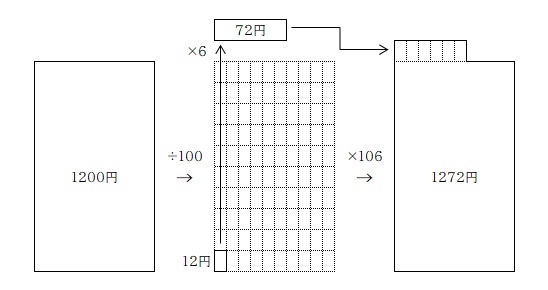
1200円の 6%: 1200×0.06=72円
1200円の 6%増(106%): 1200×1.06=1272円
身近なものなら消費税が同じように計算できますので、いろいろ試してみてください。
さぁ!割合の計算について「なるほど!」って思える勉強はできましたか?
理解できたと思えたなら問題の続きにチャレンジしてみましょう。

今年度の男子と女子の数を文字を使った数式で表してみましょう。
Let's think!
昨年度の男子の人数が x人で今年度は 4%減ということは、昨年度の人数を 100% としたときに今年度の人数は 96% になった、ということ。
x人の 100分の 96 なので、0.96x と表すことができます。
昨年度の女子の人数が y人で今年度は 6%増ということは、昨年度の人数を 100% としたときに今年度の人数は 106% になった、ということ。
y人の 100分の 106 なので、1.06y と表すことができます。

最後に、男子と女子の数の和が合計になるので、

これで方程式がふたつ完成したので連立方程式で解くことができますね。あとは計算だけですが、せっかくなのでやってみてください。
Let's think!
計算の途中で、計算を楽にするポイントもあったりするので説明していきます。

加減法で解いていきます。まずは②の式を100倍して少数をなくします。

次に①の式を 96倍して、②´の式と x の項を揃えます。

ここで計算をちょっと楽にする方法を。
650×96
ここの計算、生徒のノートを見るとたいていは真面目に筆算で計算しているのだけれど少し工夫すると暗算で簡単にできちゃいます。
96 をそのまま使うのではなく 96 = (100-4) に変形して計算してみましょう。
そうすれば、
650×96
↓
650×100=65000
650×4=2600
65000-2600=62400
というように暗算でもできる簡単な計算3つで終わらせることができます。650 と 96 の掛け算を暗算でするのはちょっとしんどいですよね。
ぜひ取り入れて実践してみてください。
さて、計算の続き。②´の式から①´の式を引いて y を求める。
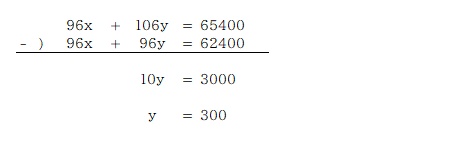
y を①の式に代入し x を求める。

A. 昨年度の男子:350人、女子:300人
数学の文章問題って苦手な子が多いけど、提示された情報をきちんと整理し理詰めで考えれば実はそこまで難しことではないと思っています。
この問題の場合、割合の計算が分からない、なんて子も多いかもしれませんが、そこもきちんと理解し、何度も実践して自在に扱えるようにしてしまえば何てことはありません。
分からないことをほったらかして逃げずに、ちゃんと分かるまで考えて自分のものにしようとする努力をしていきましょう。
----
最後におまけ。連立方程式を使わず解く考え方について。

連立方程式ではないので使う記号はひとつだけ。昨年度男子の数を x とします。男女の合計が 650人だから女子の数を 650-x というように表すことができますね。あとはそれらの数式から今年度の人数を表す数式を書いてあげれば完成。方程式③を解くだけです。
ちなみにこれって、
式① x+y=650 を変形、y=650-x とし、式②に代入している
ということ。つまり連立方程式を代入法で解いているのと同じことなんですよね。違いは、式をふたつ作ってから代入するか、式を作るときに代入した形のものを作るか。
そう考えると実は1年生の方程式の問題を解いているときすでに、連立方程式の代入法のようなことをやって問題を解いていたんですね。
色々考えてみると新しい発見が見つかって面白いかもしれませんね。
問題を解けば終わり、答えが分かれば終わり、ではなく、問題を解く過程でたくさんの「なんだろう?」っていう疑問を見つけて、それを理解していく努力が勉強です。
そしてその「なんだろう?」を解き明かしたときの達成感を味わうのが勉強の醍醐味です!
ぜひたくさんの「分からない」を見つけて、それを「分かった!」に変えていく努力をしていってくださいね!
以上です。お疲れさまでした!
(*ᴗˬᴗ)⁾⁾
2022年
6月
17日
金
「分からない」を考えよう! #8
生徒たちの「分からない」を取り上げて考えていきます。
解き方が分からない前提で「どんな風に考えて解いていくか」という過程を書いていくので、ぜひご自身でも解き方を考えながら読み進めてみてください。
今回は、とある中学のワークからの出題、数学(2年 連立方程式) の問題です。
問題

この問題は、連立方程式の章の中で出題されていた問題です。問題の中にある「解が無数にある」と「解なし」を理解するのにどうすればいいかを色々と考えていました。
多分、それを理解しようとするなら一次関数のグラフに式の線を書いて考えるのが分かりやすいのではないか、と思うのですが、この問題が出題された時点では当然まだ一次関数を学んではいないので、「解・無数」と「解・なし」を理解するのはなかなか難しいかもしれませんね。
まぁ、それは一旦置いておいて、まずはチャレンジ!
Let's think!
さて、どういうふうに進めるか。
いろいろ考えたのだけれど、とりあえず解答・解説を見てみましょうか。
解答・解説

この解説を読んで理解できるかどうか、です。
問題を解くときに「解答を見る」というのはダメなこと、悪いこと、そういうイメージがあるかもしれないですが、きちんと理解するためのアプローチとしては「解答を見る」のは全然アリです。
「解答を見る」ことがダメなのではなく、
「解答を見て、答えを写して終わらせる」ことがダメなのです。
解答を見てからが勉強です。
解答を見て、問題を解く考え方を理解しようする努力をしているかどうか。
勉強ができる子と、できない子の差が付くポイントのひとつです。
勉強ができる側に立ちたい!と思うのならぜひ実践してください。
さて、言いたいこと言うのに話が逸れましたね。
正直私はこの解説を読んできちんと理解できる子は、あんまりいないんじゃないかなぁ、と思います。
けれど、とりあえずは考えてみてください。
Let's think!
それでは、連立方程式の「解・無数」と「解・なし」について、どういうことなのか。どう理解すればいいのか、考えていきましょう。
少しズルい気もしますが、連立方程式の勉強をしている時点ではまだ勉強していない一次関数の知識を使って解説していきたいと思います。
なので、この記事を読んでいる時点で「まだ一次関数の勉強をしていない」子は、一次関数の勉強をしてから読み直してみると分かりやすいかもしれません。
-----
一次関数では、
y = ax + b
という形で式を扱います。1年生のときに勉強した比例の式は「y = ax」でしたね。比例の式が原点 (0,0) を通るのに対し、一次関数の式は原点を通りません。
a:傾き
式をグラフに示したときの直線の、文字通り傾きを表しています。
b:切片
式をグラフに示したときの直線の y軸との交点、y軸上の y座標を表しています。
y軸→つまり x座標が 0 です。一次関数の式に x=0 を代入すると、
y = a × 0 + b
y = b
座標が (0,b) となり、切片 b が y軸上の y座標であることが分かりますね。
実際にグラフに書いてみます。
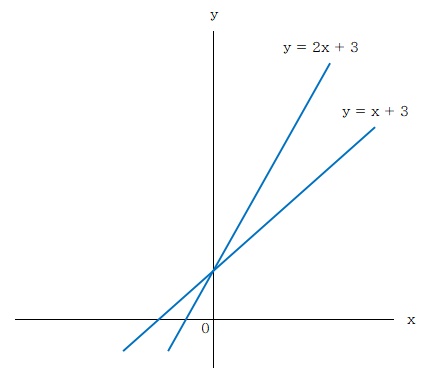
傾き a の値が変われば、直線の傾斜が変わります。
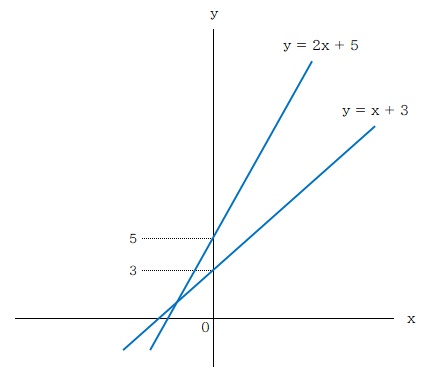
切片 b の値が変われば、y軸との交点の位置が変わります。
ザックリとですがここまでが、一次関数の式とそれをグラフに示したときの直線について、の説明です。
では、ここからは連立方程式の「解・1つ」「解・無数」「解・なし」というがどういうことかを一次関数のグラフに書いて説明します。
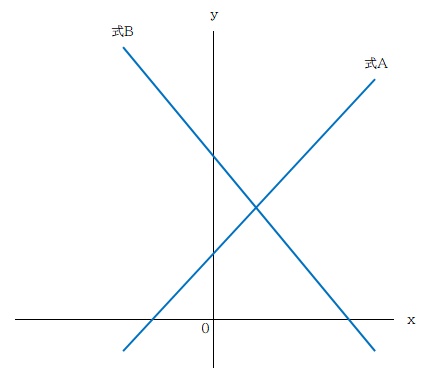
「解・1つ」
連立方程式の解は、ふたつの直線の交点の x座標と y座標を表しています。
一次関数の式の形にしたとき、傾き a の値が異なります。
同じにはなりません。
同じになる場合、というのが次に示す「解・無数」「解・なし」のケースになります。
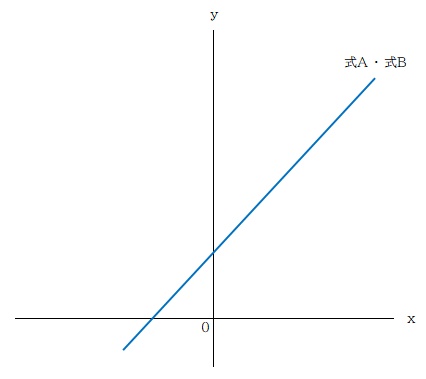
「解・無数」
連立方程式の解は「ふたつの直線の交点」ということでしたね。このようにふたつの直線が完全に重なる場合、ふたつの直線のすべてが交点となり、連立方程式の解が無数にある、ということになります。
一次関数の式の形にしたとき、傾き a の値と切片 b の値がどちらも全く同じ式、ということになりますね。

「解・なし」
連立方程式の解は「ふたつの直線の交点」ですが、このようにふたつの直線が平行になる場合、平行な2直線は決して交わることがないので解がない、ということになります。
一次関数の式の形にしたとき、傾き a の値が等しく、切片 b の値が異なる式、ということになりますね。
どうでしょうか。連立方程式の解について、グラフで示すと「なるほど!」ってなりませんか。多分、分かりやすいと思うのです。
では、ここまで学んだ内容を踏まえこの問題の解を考えてみてください。
Let's think!
それでは問題を解いていきます。
まずはふたつの式を一次関数 y=ax+b の形に直してみましょう。
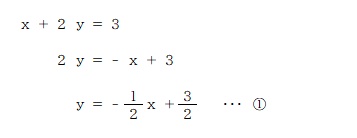
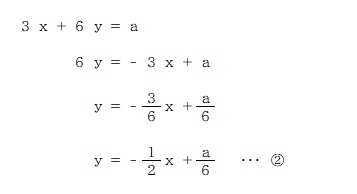
このようになりますね。
まずは、解が無数にある、とはつまり①と②の直線がぴったりと重なる状態ということでした。
傾きは①と②どちらの式も同じす。なので切片が等しくなるような値を考えれば良いですね。
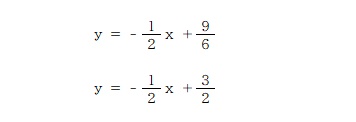
②の式に a=9 を代入してあげると①と同じ式が出来上がります。
よって「解が無数にある」のは a の値が 9 になるとき、ということになります。
そして、解がない、というのは①と②のふたつの直線が平行に並ぶ場合。つまり切片の値が同じにならなければ良いということ。
a=9 で①と②の式の切片の値が同じになる
↓
a=9 以外の値であれば①と②の式の切片の値は同じにならない
よって「解がない」のは a の値が 9 以外になるとき、ということになります。
A. (解が無数にある) a=9 のとき、(解が1つもない) a=9 以外の値をとるとき
いかがでしたか?
この記事を読んで、連立方程式の解が無数にある、解がひとつもない、ということがどういうことか理解できた!という子がひとりでもいてくれたらうれしく思います!
-----
問題を解けば終わり、答えが分かれば終わり、ではなく、問題を解く過程でたくさんの「なんだろう?」っていう疑問を見つけて、それを理解していく努力が勉強です。
そしてその「なんだろう?」を解き明かしたときの達成感を味わうのが勉強の醍醐味です!
ぜひたくさんの「分からない」を見つけて、それを「分かった!」に変えていく努力をしていってくださいね!
以上です。お疲れさまでした!
(*ᴗˬᴗ)⁾⁾
2022年
6月
13日
月
「分からない」を考えよう! #6
生徒たちの「分からない」を取り上げて考えていきます。
解き方が分からない前提で「どんな風に考えて解いていくか」という過程を書いていくので、ぜひご自身でも解き方を考えながら読み進めてみてください。
今回は、とある中学の「3年 1学期 実力テスト」で出題された、数学の問題です。
問題

(1) は簡単ですね。平均値とは、値の合計を値の数で割ったものです。なので、
(186+182+178+172+168)÷5
=886÷5
=177.2
A. (1) 177.2 cm
となります。ここは簡単。
さて、質問があったのは (2) ですね。この問題は解を考えるときに見落としやすいポイントがある、のかもしれないですね。考えてみてください。
Let's think!
まず、問題文の中にある「メジアン」という言葉。
これは「中央値」のことですね。
ちなみに、なぜ「平均値」は日本語の言葉を使うのに、「中央値」は日本語ではなく英語の言葉を使うのか、が個人的には疑問だったりするのですが、何か理由があるのかな?
まぁ、それは別にいいとして。
中央値 (メジアン) :値を小さい順に並べて、ちょうど中央にある値のこと。
具体例、まずは値の数が奇数のとき。

次は値の数が偶数のとき。

と、中央値はこのように求めます。では中央値について理解したところで問題について考えていきましょう。
d の体重が分からないので、他の 4人の体重を並べてみます。
64 , 72 , 75 , 80
ここのどこかに d の体重 x kg が入るわけですが、x がどこに入ったとしても両端の 64 と 80 が中央値になることはなさそうですね。
中央値となる可能性があるのは 72 か 75、あとは d の体重 x の 3 パターン。
実際に x に色々と数値を当てはめて見ていきましょう。



このように、
「x が 72 以下ならどこに入ったとしても中央値は 72」
「x が 75 以上ならどこに入ったとしても中央値は 75」
であることが分かりますね。あとは、
「x が 72 より大きく 75 未満で中央値は x」
となるパターンです。
よって、中央値として考えられるのは「72 , 75 , x」の 3通り!と考えてしまうと不正解になるので、ここが気を付けなければいけないポイントかな、と思います。
せっかくなので、答えが 3通りだと思ってしまった人は、ここで一度考えてみましょう。
Let's think!
中央値 x を考えるときに気を付けなければいけないポイント、それは、x が取りうる値はひとつだけか?、ということですね。
「x が中央値になる場合」
で考えを止めず、
「x が中央値になる場合、x に当てはまる値は何があるか」
まで考えないとダメですね。
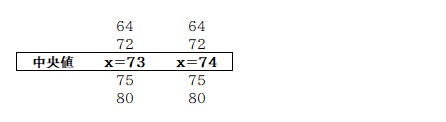
このように x が中央値になる場合、x に当てはまる値は 73 と 74 の 2通りが考えられます。
よって中央値として考えられるのは「72 , 75 , x (73 , 74)」の 4通りとなります。
A. (2) 4通り
分からないと質問があったのはこの問題だけですが、せっかくなのでここでは最後の (3) も考えてみましょう。
Let's think!
まずは、誤った値のままの場合の中央値と、正しい値に基づき修正された中央値 (182) について考えてみます。

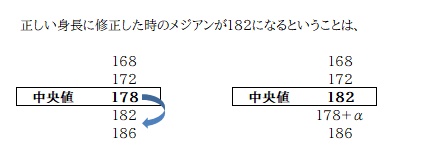
修正前の中央値は 178 で、修正後 182 になったということは、
「168/172/178 のいずれか (おそらく178) が誤りで、正しい数値は 182 より大きい」
ということが考えられますね。
では次に平均値について考えてみます。
(1) の解より 5人の身長の平均値は 177.2 だがこれが誤りで、正しい数値に基づく 5人の身長の平均値は 178.2 となる。
平均値(誤) と 平均値(正) の差は 178.2-177.2=1 なので、5人の平均が 1cm 増えたということは、身長の合計が 5cm 増えたということ。
5人の身長のうち、5cm 増えることで 182 より大きくなるのは、と考えれば答えが分かりますね。
A. (3) 誤っている値 178 cm / 正しい値 183 cm
ちなみに補足。
上記で、誤った値を 168/172/178 のうち 178 がおそらくそうであると考えた理由。
分かりますか?
もし 168 が誤りで正しい数値が 182 より大きくなる場合を考えると、168 だけでなく 172 と 178 も正しい数値が 182 より大きくなる可能性が出てきて、168/172/178 のうちどれが誤った値なのかを特定することができなくなります。
なので正しい平均値から具体的に何 cm 変化があったのかの計算をする前に、誤った値はおそらく 178 かな、と考えたということです。
問題をただ解くだけでなく、問題を解く過程でこんな風にいろいろ考えることが論理的な思考力を養っていくことにつながります。
少しでも楽に解くにはどうすればいいか、だとか、ちょっとの疑問でもトコトン考える!そういう勉強を心がけてください。
-----
問題を解けば終わり、答えが分かれば終わり、ではなく、問題を解く過程でたくさんの「なんだろう?」っていう疑問を見つけて、それを理解していく努力が勉強です。
そしてその「なんだろう?」を解き明かしたときの達成感を味わうのが勉強の醍醐味です!
ぜひたくさんの「分からない」を見つけて、それを「分かった!」に変えていく努力をしていってくださいね!
以上です。お疲れさまでした!
(*ᴗˬᴗ)⁾⁾
2022年
6月
07日
火
「分からない」を考えよう! #5
生徒たちの「分からない」を取り上げて考えていきます。
解き方が分からない前提で「どんな風に考えて解いていくか」という過程を書いていくので、ぜひご自身でも解き方を考えながら読み進めてみてください。
今回は、とある中学の「3年 1学期 実力テスト」で出題された、数学の問題です。
問題

なかなか難問ですね。解き方を知らない問題はワクワクします。解き方を知っていればただの作業ですからね。
それではチャレンジしていきましょう!ご覧の皆様もまずは考えてみてください。
Let's think!
問題文を読んで、書いてあることを正しく理解するだけでも難しい、と感じる子もいるかもしれないですね。
(1) は問題にある [ ] で挟んだ数字が何を意味するのか、問題文を読んでちゃんと理解できたかどうかを確認する問題、といったところでしょうか。
問題として出されているのは [10213] なので、この値を求めるには 10213 を 7 で割ったときの余りを求めればよい、ということになります。
10213 ÷ 7 = 1459 … 0
割り切れましたね。よってこの問題の解は、
A. 0
となります。さて、ここまでは問題の意味が理解できたか、の確認作業。いわば前座のようなもの。次の問題が本番ですよ!
Let's think!
さて、(2) ですが、私の場合はとりあえず数字の小さいものからいくつか計算してみることにしました。2~5乗くらいまでなら計算にさほど時間もかからないと思います。
頭の中だけで考え込むより、考えたことはすぐに手を動かしアウトプットする。トライ&エラーの繰り返しの中から問題を解くためのヒントを見つけ出します。

5乗まで計算してみて、あることに気付きます。余りが 1, 6, 1, 6 と繰り返していますね。これは大きなヒントになる気がしました。
もちろん、たまたまここまでは繰り返しになっているが 6乗の余りは違う数字になるかもしれません。
ですので、今度はこの「余りの 1 と 6 が繰り返していく」という法則が正しいことの証明について考えていく必要がありますね。
その方法の一つに、6乗、7乗、8乗とすべて計算して力ずくで解を見つける、という手段もあるといえばありますが、私はそこまで大きな数の計算はしたくないのでやりません。
というわけで、続きを考えてみてください。
Let's think!
まず、(6の2乗) の余りは 1 です。
これはつまり「(6の2乗)-1」は 7の倍数である、というように言い換えることができます。
(6の2乗)-1
→7の倍数である。7 で割ると 1 余る、ということを表している。
これを元に考えていきます。
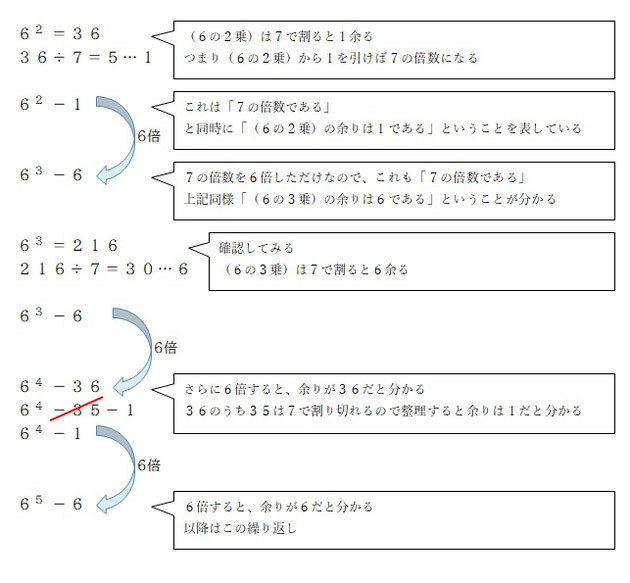
私の場合は、こんな感じで考えをまとめました。
これで、6 の偶数乗の余りは「1」、6 の奇数乗の余りは「6」、であることが証明できたと思います。
よって、6 の x乗のうち、余りが 1 となる 2桁で最小のもの、その解は、
A. x=10
となります。
さて、私なりに考えて、私なりの解き方を書かせていただきましたが、実際どうなんでしょうね。この問題を作られた先生の解説を聞いてみたいです。
もっとシンプルな考え方があるのかもしれません。
これだけのことを考え整理するのにもそれなりの時間がかかりますから、たとえば推測と力技の組み合わせで、
1. 6 の 2~5乗を計算、7で割って余りを求める
2. 余りが 1, 6, 1, 6 続くことから、10乗の余りが 1 になる可能性が高いのではないか、と仮説を立てる。
3. 仮説の実証のため 6 の 10乗を計算し 7 で割って余りを求める
4. 計算を間違えなければ余りは 1 となるので解が x=10 と求めることができる
という解き方でもいいのかもしれません。6 の 10乗の計算にどれだけ時間がかかるかは、やっていないので分かりませんが。
面白い問題だったので是非いろいろ考えてみてください。
ちなみにおまけ。エクセルを使った 6 の x乗の計算結果です。
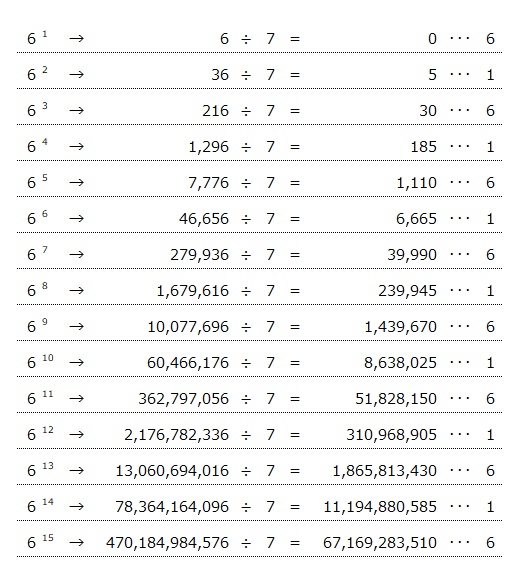
こういうもの簡単に作ることができます。エクセル、便利ですね。そして、こうして見ると 6 の 10乗くらいなら計算もそこまで苦にはならない気がしますね。
-----
問題を解けば終わり、答えが分かれば終わり、ではなく、問題を解く過程でたくさんの「なんだろう?」っていう疑問を見つけて、それを理解していく努力が勉強です。
そしてその「なんだろう?」を解き明かしたときの達成感を味わうのが勉強の醍醐味です!
ぜひたくさんの「分からない」を見つけて、それを「分かった!」に変えていく努力をしていってくださいね!
以上です。お疲れさまでした!
(*ᴗˬᴗ)⁾⁾
2022年
5月
31日
火
「分からない」を考えよう! #2
生徒たちの「分からない」を取り上げて考えていきます。
解き方が分からない前提で「どんな風に考えて解いていくか」という過程を書いていくので、ぜひご自身でも解き方を考えながら読み進めてみてください。
今回は、とある中学の「2年 1学期 中間テスト」で出題された、数学(式の計算) の問題です。
問題
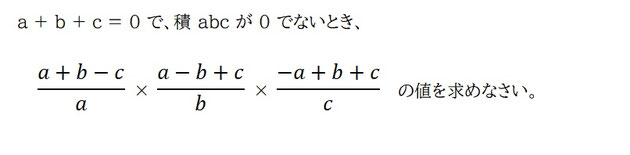
今回のテスト問題を見た中で個人的に「一番面白そう!」と思った問題です。ちなみに、その生徒のクラスで正解できたのは3人だけだったそうです。
さて、一番面白そう、と思った理由はパッと見て解き方が分からなかったから!
なのでワクワクしながら挑戦スタートです。
まず、解き方は分からない、が、上手いこと式を整理してあげれば良いんだろうな、ということは分かっていました。問題はどういう整理の仕方をするか、ですね。
こういうときは、
(1) とりあえずこの問題は飛ばして解ける問題を解いていく。
(2) とりあえずできる計算をやってみる。
その過程でこの問題を解くヒントが見つかるかもしれません。私はとりあえず、そのまま計算してみました。頭の中だけで考え込むより、まずは手を動かすのが性に合っています。
Let's think!
とりあえず計算してみたら、いろいろ打ち消しあっていい感じに整理されたら良いなー、と思いつつ、一方では多分これじゃ無理だろうなー、とも思いながら計算してみました。
計算しつつも、頭の中では式を整理するための工夫を考えながら。
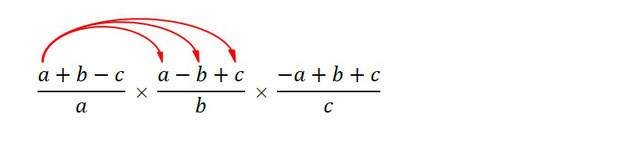
こんな感じで、本当にただ計算して整理してみます。

ここまで計算してみましたが、赤丸の同類項を整理してもこれ以上はどうにもならなそうですね。そもそもこの計算をするだけで時間がかかり過ぎていて、時間制限のあるテストの中ではこんなことをしている余裕はないでしょう。
正面突破は無理、ということが分かりました。
そこで問題文を最初から見直すと、そういえばもう一つ式あるよね、ということに気づきます。
a+b+c=0
実はこの式こそが問題を解くためのカギ!問題の式の中に a+b+c があれば 0 を代入することができます。ですが、問題の数式の分子の部分には、
a+b-c 、a-b+c 、-a+b+c
というように、どれもマイナスが入っていて代入することができません。マイナスの項が邪魔です。なので、ちょっと整理してみました。
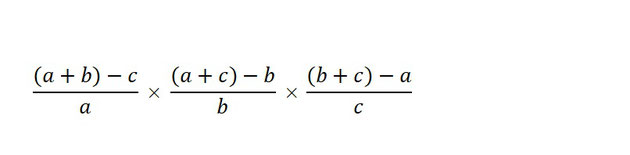
私の場合はここでピンときました。
a+b+c を代入できる個所は無い、けれど a+b だけなら代入できそうです。a+c 、b+c も同様です。
問題を解くためのカギ(a+b+c=0)はある。でもこのままでは問題のカギ穴には合わない。じゃあカギの形のほうを変えてしまえば。さて、それでは、
Let's think!
問題文にある a+b+c=0 を次のように変形させます。
a + b = -c
a + c = -b
b + c = -a
この形であれば代入して計算していくことができますね。
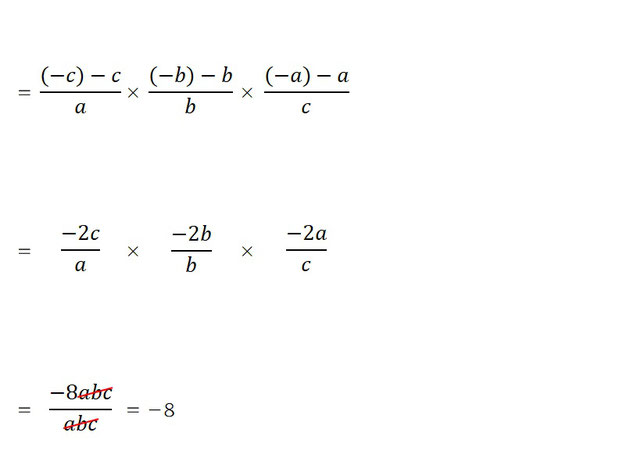
A. -8
キレイに整理され解くことができましたね。
-----
問題を解けば終わり、答えが分かれば終わり、ではなく、問題を解く過程でたくさんの「なんだろう?」っていう疑問を見つけて、それを理解していく努力が勉強です。
そしてその「なんだろう?」を解き明かしたときの達成感を味わうのが勉強の醍醐味です!
ぜひたくさんの「分からない」を見つけて、それを「分かった!」に変えていく努力をしていってくださいね!
以上です。お疲れさまでした!
(*ᴗˬᴗ)⁾⁾
2022年
5月
30日
月
「分からない」を考えよう! #1
生徒たちの「分からない」を取り上げて考えていきます。
解き方が分からない前提で「どんな風に考えて解いていくか」という過程を書いていくので、ぜひご自身でも解き方を考えながら読み進めてみてください。
今回は、とある中学の「2年 1学期 中間テスト」で出題された、数学(式の計算) の問題です。
【問題】

表の中の数字 N を、その数字の位置を表す座標 x,y の値から求める式を考えれば良いんだな、みたいなことをまず考えることができればいいですね。
そこでまずは数字の変化に規則性はないか、探してみましょう。
Let's think!
数字の変化の規則性、見つけることができましたか?
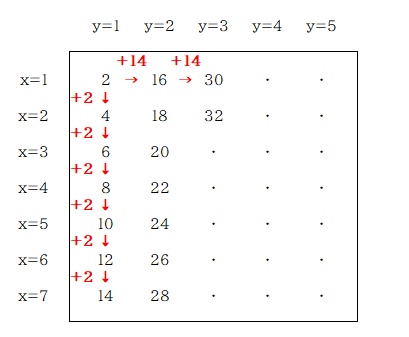
数字は偶数が順に並んだものなので 2 ずつ増えていきます。1つの列に 7つ並べたところで次の列に移ります。なので横の数字を見ると 14 ずつ増えているのが分かりますね。
では、この規則的な変化を x と y を使って表す数式を作っていきましょう。
Let's think!
まず縦方向の数式は簡単に思いつくと思います。

x=1 のときが 2 で、そこから x が 1 増えるごとに 2 ずつ増えていくので、シンプルに 2x という式が成立しますね。
ではさらに横の変化、y を絡めた式を作りましょう。

ヒントその1、です。
1行目だけを見て考えてみます。2、16、30、という数字を先に考えた 2x と合わせて作ることができればいい。1行目なので 2x に x=1 を代入し 2x=2 となります。
よって、横の数字を「x を使って求める数」と「y を使って求める数」に分けると、
2+0 、2+14 、2+28 と表すことができますね。
この 0 、14 、28 の部分を、y の値を使って求める式を作っていきます。
Let's think!
y を使った数式を作ることができましたか?できなかった人のためのヒントその2、です。

「2x+〇〇」の ○○ の部分を少し分解して考えてみます。
最初に変化の規則性を考えたときに、横の数字は 14 ずつ増えていると考えたのを思い出してみましょう。
14 の個数がいくつになるか、を考え、その個数を求める式を y の値を使って求める数式を考えるようにすると、すごく分かりやすくなったと思いませんか?
整理すると、
「2x+〇〇」の ○○ の部分を求める数式を考える
↓
「2x+(14×〇〇)」の ○○ の部分を求める数式を考える
ということになりますね。では、最後です。y の値を使って 〇〇 の部分を求める数式を作ってみましょう。
Let's think!
「2x+(14×〇〇)」の ○○ の部分、14 の個数を求める部分の数式は、
y=1 のとき 0 、y=2 のとき 1 、y=3 のとき 2
となる。つまり「y の値より 1 小さい数」ということが分かるので y-1 とすれば求めることができますね。
よって N を求めるための数式、その答えはこのようになります。
N = 2x + 14(y-1)
では、これが正しいか確認です。問題文にある N(3,2) を代入して解が 20 になるかどうか。他にも適当に N(5,2) とか N(1,3) とか試してその位置の値を求めることができれば ok ですね。
この数式さえ完成してしまえばあとは簡単。
(1) N(3,5) を代入して値を求める。
(2) x=1 を代入して式を整理する。
Let's think!
(1) N(3,5) を代入して値を求める。
N = 2x + 14(y-1)
N = 2×3 + 14(5-1)
N = 6 + 14×4
N = 6 + 56
N = 62
A. 62
-----
(2) x=1 を代入して式を整理する。
N = 2×1 + 14(y-1)
N = 2 + 14y - 14
N = 14y - 12
A. N = 14y - 12
ちなみに、この問題の答えの数式が何を表すものなのか?っていうのは分かりますか?
この式は「1行目限定で y 列目の値を求める数式」です。
-----
問題を解けば終わり、答えが分かれば終わり、ではなく、問題を解く過程でたくさんの「なんだろう?」っていう疑問を見つけて、それを理解していく努力が勉強です。
そしてその「なんだろう?」を解き明かしたときの達成感を味わうのが勉強の醍醐味です!
ぜひたくさんの「分からない」を見つけて、それを「分かった!」に変えていく努力をしていってくださいね!
以上です。お疲れさまでした!
(*ᴗˬᴗ)⁾⁾
2019年
11月
03日
日
文章問題の考え方講座 ~part5~
今回は連立方程式の範囲の問題です。
式を解くのに必要なのは連立方程式の知識ですが、式を立てるのに必要なのは「時間」「角度」「単位量あたりの数」あたりの考え方でしょうか。
では、問題がこちら。
------------------------------------------------
7時x分 の長針と短針の位置が、2時y分 で入れかわるとき
(1) x と y についての連立方程式を立てなさい。
(2) x の値を求めなさい。
------------------------------------------------
まずは問題における「7時x分の長針と短針の位置が、2時y分で入れかわる」というのが、どういう状態なのか。ここをきちんと理解し、イメージできなければダメですね。
長針と短針の位置が「7時x分」と「2時y分」で入れかわるということは、
短針(時間を示す針)の位置が、
「7時x分」→「7」と「8」の間
「2時y分」→「2」と「3」の間
となるので、
長針(分を示す針)の位置は、
「7時x分」→「2時y分」における長針の位置、つまり「2」と「3」の間
「2時y分」→「7時x分」における長針の位置、つまり「7」と「8」の間
となりますね。

図にするとこんな感じです。
「7時x分の長針」と「2時y分の短針」
「7時x分の短針」と「2時y分の長針」
がそれぞれ等しい位置にあるということですね。
あとはそれぞれの位置を数式で表すことができれば等式を二つ書くことが可能です。
で、長針と短針の位置を表わすのに用いるのが角度。
「12」の位置、つまり 0時を起点として長針および短針の位置までの角度を「x分」「y分」を使って表わすことができないか?
という発想に辿り着けばあとは簡単。

まずは長針の角度を考えます。
長針は 60分で 1周 (360°) 回るので、
360÷60=6
長針が 1分あたりに動く角度は 6° です。なので、
7時x分 の長針の角度は「6x」
2時y分 の長針の角度は「6y」
と表すことが出来ます。

次に短針の角度。
短針は 60分で時計の数字1つ分、つまり 1時間あたり (30°) 動くので、
30÷60=1/2
短針が 1分あたりに動く角度は 1/2° です。なので、
7時から x分 経ったときの短針の角度は「1/2x」
2時から y分 経ったときの短針の角度は「1/2y」
と表すことが出来ます。
ただし、短針は 0時からの角度も考えないといけません。

短針は 1時間あたり (30°) だから、
0時から 7時までの角度は「210°」
0時から 2時までの角度は「60°」
です。ここは簡単ですね。

あとは、
「0時 から 7時 の角度」と「7時 から 7時x分 の角度」
「0時 から 2時 の角度」と「2時 から 2時y分 の角度」
を足したものが、0時を起点とした短針の角度となります。なので、
7時x分 の短針の角度は「1/2x + 210」
2時y分 の短針の角度は「1/2y + 60」
と表すことが出来ます。
最後に、ここまでで作った「長針と短針を表わす数式」をイコールの関係にあるもの同士まとめれば完成です。

7時x分の短針の角度 = 2時y分の長針の角度
1/2x + 210 = 6y

7時x分の長針の角度 = 2時y分の短針の角度
6x = 1/2y + 60
これで (1) の問題は終了。
(2) の問題はこの2つの式を連立方程式で解くだけですね。
以上、今回の問題、解説はいかがでしたか?
中学生の皆さんは、読んでみて終わり、ではなく、ぜひ同じ問題を自分でも実際に解いてみて下さい。
実際に解いてみると、読んでいた時には気づかなかった疑問や、よく分からないことなどが見えてくることもありますので(^^)
2019年
10月
27日
日
文章問題の考え方講座 ~part4 #2~

右の図のように、
直線①:y=x/2
双曲線②:xy=6 (x>0)
2点 A(-4,3) B(-1,-1)
がある。
また、四角形ABCDが平行四辺形となるように、2点 C , D をそれぞれ①、②の上にとる。次の問いに答えなさい。
(1) 2点 C , D の座標をそれぞれ求めなさい。
(2) 点P (3,-1) を通る直線n で、平行四辺形ABCDの面積を2等分したい。
直線n の式を求めよ。
--------------------------------------------------
前回は、
「平行四辺形ABCD の中心(対角線の交点)を軸にして、点P と点対称になる点」
について考え、その点と 点P を結ぶ直線を求めました。
ちなみに、
「この直線がどうして 平行四辺形ABCD の面積を二等分する線になるのか?」というと、
点対称になる点同士を結ぶ
↓
点対称の中心を通る
↓
点対称の中心は、平行四辺形ABCD の中心(対角線の交点)
となり、「平行四辺形の中心を通るから」が答えですね。
平行四辺形を二等分する直線 = その平行四辺形の中心(対角線の交点)を通る直線
今回はこの考え方で問題を解いていきたいと思います。
まずは 平行四辺形ABCD の対角線の式を求めていきます。
(1) の問題を解いていれば 点A ~ 点D の座標は全部分かっているはずなので、
点A と 点C の座標から 直線AC の式を求める
点B と 点D の座標から 直線BD の式を求める
一次関数の式 y=ax+b にそれぞれの座標を代入して連立方程式で解けば良いですね。

直線AC と 直線BD の交点の座標を求める
この座標が対角線の交点、つまり 平行四辺形ABCD の中心ですね。

最後に、
平行四辺形ABCD の中心の点 と 点P を結ぶ 直線n の式を求める
となります。
前回の解き方よりかなり手順が多いですね。全部で連立方程式を4回も解かないといけません。と、考えると面倒なだけのように思うかもしれませんが、「入試に向け連立方程式の計算の復習も出来る」と捉えればこちらの解き方を選ぶことにも価値が生まれますね。
全ては捉え方次第。
ぜひ色々な考え方で問題を解き数学を楽しんでください(^^)
2019年
10月
26日
土
文章問題の考え方講座 ~part4 #1~
前回(part3 #2)の続き。
今回は (2) の問題について考えていきます。
解説するのが (1) から (2) の問題に変わるので part も新しくしますね。
-------------------------------------------------

右の図のように、
直線①:y=x/2
双曲線②:xy=6 (x>0)
2点 A(-4,3) B(-1,-1)
がある。
また、四角形ABCDが平行四辺形となるように、2点 C , D をそれぞれ①、②の上にとる。次の問いに答えなさい。
(1) 2点 C , D の座標をそれぞれ求めなさい。
(2) 点P (3,-1) を通る直線n で、平行四辺形ABCDの面積を2等分したい。
直線n の式を求めよ。
--------------------------------------------------
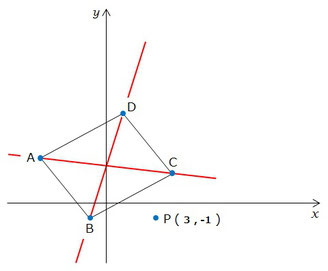
グラフに 点P を追加するとこんな感じですね。

平行四辺形ABCD の面積を半分にする直線、なので、
「平行四辺形ABCD の中心(対角線の交点)を軸にして、点P と点対称になる点」
を求めて、点P と結べば二等分に出来ますね。
点P と点対称な点を「点Q」とします。
点Q は、「点P が 点B からどれだけ移動した場所にあるか」という位置情報をもとに、「点D (点B と点対称な点) から逆向きに同じだけ移動した場所」を考えることで求めることが出来ますね。

点P は 点B から「x軸プラス方向に 4」移動した位置にあることが分かるので、点D から「x軸マイナス方向に 4」移動した位置に 点Q を作れば良いですね。

(1) の問題が解けていれば 点D の座標はすでに計算済みのはずですので、そこから 点Q の座標も求めることが出来ます。
あとは 点P / 点Q の座標を y=ax+b にそれぞれ代入し、連立方程式を解いて a / b の値を求めれば 直線n の式の完成ですね。

さて、今回の解説もきちんと伝わったでしょうか?
次回はこの問題を別のアプローチで解いていきたいと思います(^^)
2019年
10月
25日
金
文章問題の考え方講座 ~part3 #2~

右の図のように、
直線①:y=x/2
双曲線②:xy=6 (x>0)
2点 A(-4,3) B(-1,-1)
がある。
また、四角形ABCDが平行四辺形となるように、2点 C , D をそれぞれ①、②の上にとる。次の問いに答えなさい。
(1) 2点 C , D の座標をそれぞれ求めなさい。
(2) 点P (3,-1) を通る直線n で、平行四辺形ABCDの面積を2等分したい。
直線n の式を求めよ。
--------------------------------------------------
この問題の (1) ですね。
前回は、点C / 点D それぞれの x座標と y座標、それら4つの値を文字2つで表して連立方程式で解く、という考え方でした。
点C の座標を (X,Y) とし 点D の座標を X と Y を使って表わしましたね。
今回は、点C の座標を文字1つだけで表わす考え方です。
それほど難しいことではないです。点C は 直線① 上にあるのだから、例えば 点C の x座標が分かるのであれば 直線① の式に代入することで y の値を求めることが出来ますよね。
つまり、点C の x座標 = t とした場合、直線① の式 y=x/2 に代入して y=t/2、y座標 = t/2 と表わせます。
あとは前回同様、点C の座標 (t,t/2) から 点D の座標を書くと、

このように表わすことが出来るので、あとは 点D の座標を 双曲線② の式に代入し t の値を求めれば良いですね。
ちなみに前回と今回の解き方、何が違うかと言うと「代入のタイミング」だけなんですよね。
分かるでしょうか?
【前回】※扱う文字は X,Y から t,u に変更してます。
C (t,u) とする。
D (t-3,u+4) となる。
C/D の値を式に代入。直線①:u=t/2、双曲線②:(t-3)(u+4)=6
直線① と 双曲線② の式を連立方程式(代入法)で解く。(t-3)(t/2+4)=6
【今回】
C の x座標 t とする。
直線① に代入し y座標を作る。y=t/2
D (t-3,t/2+4) となる。
双曲線② に代入し方程式を解く。(t-3)(t/2+4)=6
という感じで、結局どちらも同じ式(二次方程式)を解くことになります。
さて、今回の解説もきちんと伝わったでしょうか?
次回は (2) の問題の解説を書いていきたいと思います(^^)
2019年
10月
24日
木
文章問題の考え方講座 ~part3 #1~
part3は二次方程式の単元の中で出題されてた問題です。
けれど、連立方程式、比例反比例、一次関数、図形(平行四辺形)の性質、など複合的な知識の土台が無ければ解けないかな、という感じの問題ですね。
--------------------------------------------------

右の図のように、
直線①:y=x/2
双曲線②:xy=6 (x>0)
2点 A(-4,3) B(-1,-1)
がある。
また、四角形ABCDが平行四辺形となるように、2点 C , D をそれぞれ①、②の上にとる。次の問いに答えなさい。
(1) 2点 C , D の座標をそれぞれ求めなさい。
(2) 点P (3,-1) を通る直線n で、平行四辺形ABCDの面積を2等分したい。
直線n の式を求めよ。
--------------------------------------------------
今回はこの問題の (1) を解説していきたいと思います。
まずは、四角形ABCD が平行四辺形であるということ。そのことから 点C と 点D の位置関係をどのように捉えるか、が大切なポイントになります。

四角形ABCD が平行四辺形だということは、
線分AB と 線分DC は「傾き」も「長さ」も等しい
ということになりますね。つまり、
「点C から 点D の位置関係」は「点B から 点A の位置関係」と等しい
と考えることが出来ます。

点A と 点B の座標は分かっているので、点A は 点B から見て、
「x軸マイナス方向に3 , y軸プラス方向に4 移動した位置」
にあることが読み取れます。つまり、

点C と 点D の位置関係もそれと同様なので、点D は 点C から
「x軸マイナス方向に3 , y軸プラス方向に4 移動した位置」
にあるということになります。
この位置関係の情報を利用すると、点C および 点D の座標を文字を使った式で表すことができます。

点C を (X,Y) とした場合であれば、点D は (X-3,Y+4) というようにそれぞれの座標を「文字2つ」で表わすことが出来ます。
もし 点D を (X,Y) とするのであれば、点C は (X+3,Y-4) となりますね。まぁそれは、どちらの点を基準にするか、というだけのことなのでどちらでもOKです。
あとは、直線① の式に 点C の座標を、双曲線②の式に点Dの座標を、それぞれ代入して解いていけばいいだけです。
この手の問題の考え方のポイントは、
点C の x座標 (?1)、点C の y座標 (?2)、点D の x座標 (?3)、点D の y座標 (?4)
と、不明な値が4つあるわけですが、
?1 → 文字1、?2 → 文字2、?3 → 文字3、?4 → 文字4
このように、それぞれに文字を割り当てるのではなく、
?1 → 文字1、?2 → 文字2、?3 → 文字1を使って表わす、?4 → 文字2を使って表わす
こうして扱う文字の数を2つにするということ。
扱う文字が2つであれば連立方程式で解くことが出来ます。
ちなみに、扱う文字が1つであれば方程式で解くことが出来ます。ということで、次回は少し違った考え方で解く方法を解説してみたいと思います(^^)
2019年
10月
15日
火
文章問題の考え方講座 ~part2~
ようやくpart2です。今回の問題はこちら。
--------------------------------------------------
電車が分速640mで等しい間隔をおいて走っている。A君が線路に沿って歩いたとき、前から来る電車には7分ごとにすれ違い、後ろから来る電車には9分ごとに追いこされた。A君の歩いた速さを求めなさい。
--------------------------------------------------
この問題を解くための一番シンプルな考え方は、
①:「A君」の歩く速さを a(m/分)とする。
②:「電車」と「A君」がすれ違う瞬間から7分後の、「電車」と「A君」との間の距離を文字式で表す。
③:「電車」が「A君」を追いこす瞬間から9分後の、「電車」と「A君」との間の距離を文字式で表す。
④:②と③の文字式をイコールで結び方程式を解く。
このような感じでしょうか。
実はこれだけだと不十分でこの問題の要点を正しく理解することは出来ないのですが、ひとまず「A君」と「電車」との関係を図に書いてまとめてみます。

②電車の速さは640m/分なので電車の走った距離は、640×7=4480(m)。A君の歩いた距離は、a×7=7a(m)。これらを足したものがすれ違う場合の「電車」と「A君」との間の距離です。
4480+7a
③電車の走った距離は、640×9=5760(m)。A君の歩いた距離は、a×9=9a(m)。これらの差が追いこす場合の「電車」と「A君」との間の距離です。
5760-9a
ということで、あとはこの二つの文字式をイコールで結んで計算すればいいわけですが、質問をくれた生徒が分からなかったことは、
「どうしてこの二つの式が等しくなるのか?」
ということでした。
二つの式が等しい、とする根拠は問題に書いてある通り、電車は「等しい間隔をおいて走っている」からです。
ではなぜ「電車とA君との間の距離」とそのことが結びつかないかというと、式を作るときに最初の電車とA君との関係しか見ていないから。
なぜ7分後、9分後の距離を考えるのか。
A君が最初の電車とすれ違う瞬間から7分経った瞬間がどういう状況になっているのか、追いこす場合も同じです。9分後にどういう状況になっているのか。そこが正しくイメージできていないから二つの式が等しくなる理由が分からないのだと思います。
ということで、この問題を解くための考え方を改めて図にまとめます。

問題文「前から来る電車には7分ごとにすれ違い」は、
A君が最初の電車とすれ違う瞬間から7分後 → 次の電車とすれ違う瞬間
問題文「後ろから来る電車には9分ごとに追いこされた」は、
A君を最初の電車が追いこす瞬間から9分後 → 次の電車が追いこす瞬間
だということを正しく理解しイメージできないと「式の作り方は知ってる」けど「なぜ等しい関係になるのか分からない」ということになるのですね。
もちろんこの問題を解くだけであれば「なぜ電車とA君との間の距離が等しくなるのか?」について分からないままでも支障はないです。
ただそれは「この問題を解くためだけの知識」でしかなく応用は効きません。
だから当塾では「解き方」ではなく「なぜその解き方なのか」ということを、正しく理解できるよう指導することに力を入れているのです(^^)
2019年
10月
14日
月
文章問題の考え方講座 ~part1 #4~
今回もこれまで(文章問題の考え方講座 ~part1 #1~ / ~part1 #2~ / ~part1 #3~)と同じ問題を題材に、また少し違った解き方について考えていきたいと思います。
この問題の解き方を考えるのはこれで最後です。次回からは別の問題を考えていきますね。
--------------------------------------------------
ある中学校の昨年の生徒数は、男女あわせて530人であった。今年は、昨年と比べると、男子は5%減り、女子は8%増え、合計では6人増えている。今年の男子と女子の生徒数を、それぞれ求めよ。
--------------------------------------------------
さて、この問題は連立方程式の問題ということで2年生のワークに収録されている問題なのですが、文章問題が苦手な子には「決められた解き方通りに解く」のではなく、とにかくいろいろ考えてもらいたいので、
「使う文字をxとyの2つではなく、xだけを使って解いてみて!」
と、文章問題が苦手な子には少々しんどいと感じるであろう無茶振りをしたりします。
考え方は特に難しいことはないです。
去年の男子をx人、去年の女子をy人、とすると、

このように考えたわけですが、この内「y」が使えなくなったので、「去年の女子の人数」をどのように表わすか?ということを考える必要がありますね。
去年の合計が530人、去年の男子がx人。なので、
「去年の女子の人数」=「合計から男子の人数を除いた人数」
と、これだけ考えることが出来ればいいわけです。

あとは出来上がった方程式を解けばいいだけですね。
さて、「文章問題の考え方講座」と題して一つの問題の考え方を4回にわたって書いてきましたが、こんな風に色々な解き方を考えさせることで、文章問題は苦手な子どもたちでも段々と「自分で解き方を考える力」が身についていきます。
「問題の解き方を覚える学習」はどれだけやっても社会に出たとき役には立ちませんし、なにより面白くないと私は思います。
ぜひ色々な解き方、考え方を模索して楽しんでみて下さい(^^)
2019年
9月
11日
水
文章問題の考え方講座 ~part1 #3~
今回もこれまで(文章問題の考え方講座 ~part1 #1~ / ~part1
#2~)と同じ問題を題材に、また少し違った解き方について考えていきたいと思います。
--------------------------------------------------
ある中学校の昨年の生徒数は、男女あわせて530人であった。今年は、昨年と比べると、男子は5%減り、女子は8%増え、合計では6人増えている。今年の男子と女子の生徒数を、それぞれ求めよ。
--------------------------------------------------
この問題、こんな式を書いて間違う子もいます。
昨年の生徒数、男子をx人、女子をy人とし
x+y=530
0.95x+1.08y=6
なぜこうなったのかは分かりませんが、おそらく解き方は知っていてその解き方に当てはめる値を深く考えずに問題の中から拾っていった結果、
今年の男子と女子の生徒数の合計、の式が「0.95x+1.08y=6」となってしまったのかもしれませんね。
問題の中にある「6」という値は、昨年と比較し今年の全体の生徒数が6人増えた、ということなので、今年の生徒数「男子(0.95x)」「女子(1.08y)」の合計とするなら、昨年の合計530人に増えた6人を足して536人にしなければ等式は成立しませんね。
こういう間違いも子どもたちの学びにおける大切な素材です。上記に書いた通り、
「二つ目の式の左辺を “0.95x+1.08y” とするなら右辺はどのような数を置くべきか?」
については当然指導し学んでもらいますが、当塾ではそこから先に一歩踏み込んで、
「二つ目の式の右辺が “6” になるような左辺の式を考えてみよう!」
という問いかけをして、子どもたちに解き方を考えるよう促します。
この場合、「6」という値が何を表わしているかを読み解く必要があります。
昨年の人数と比較したときの今年の人数の変化は、
男子 → 5%減った
女子 → 8%増えた
全体 → 6人増えた
男子は減って女子は増えて、けど全体では人数が増えている、ということは「減った男子の人数」より「増えた女子の人数」の方が多いから全体で6人増えている。
つまり「増えた女子の人数」と「減った男子の人数」との差が「6人」ということ。
なので、
「増えた女子の人数」ー「減った男子の人数」= 6
で等式が成立します。
昨年の人数は男子を x人、女子を y人としていて、男子は「昨年の人数の 5%」が減った人数、女子は「昨年の人数の 8%」が増えた人数。なので、
「減った男子の人数」=0.05x
「増えた女子の人数」=0.08y
これで等式を完成させることが出来ますね!
さて、今回の考え方はいかがでしたか?
方程式の解き方って考え方次第で色んな式を書いて解くことが出来て面白いと思いませんか?
用意された解き方に囚われず自由な発想で自在に思考を広げることが出来る、子どもたちにはそういう学力を身につけていって欲しいですね(^^)
2019年
7月
25日
木
文章問題の考え方講座 ~part1 #2~
第2回は前回(文章問題の考え方講座 ~part1 #1~)と同じ問題を題材に、けれど少し違った解き方について考えていきたいと思います。
--------------------------------------------------
ある中学校の昨年の生徒数は、男女あわせて530人であった。今年は、昨年と比べると、男子は5%減り、女子は8%増え、合計では6人増えている。今年の男子と女子の生徒数を、それぞれ求めよ。
--------------------------------------------------
この問題、解き方を覚えてなぞるだけの子たちがよくやるのが、「今年の男子と女子の生徒数」を「x , y」とおいて解こうとすること、ですね。
もちろんそれでも解くことは出来ますが、何%増えた減った、という変化が昨年の人数を元にしているので、今年の人数を基準に考えようとすると少し難易度が上がります。
で、どういう式を書けばいいか分からずに困り果てている子たちが非常に多いです。
「今年の男子と女子の生徒数」を「x , y」とおいて
「昨年の男子と女子の生徒数」を「x , y」を使って表わす
となるのですが、ここで必要なのが「○%増えたり減ったりしたものを、増えたり減ったりする前に戻す」計算の考え方ですね。
要するに「税込み価格を、税抜き価格に戻す」計算、と言えば分かりやすいかな。
この考え方が分からない子はとても多くて、
例えば、
男子が5%減った → 5%増やせばいい
1.05x
女子が8%増えた → 8%減らせばいい
0.92y
というような考え方で間違った式を書く子が割と多いです。
しかし「昨年の人数を元にした5%」と「今年の人数を元にした5%」というのは、値が同じ「5%」であっても、その中身は別物です。
この問題ではあくまでも「昨年の人数」を100%として考えなければなりません。
昨年の人数を「x , y」として今年の人数を表わすと、

こうでしたね。100だったものが95に、100だったものが108に、という変化をもう少し分かりやすく書くと、

このような感じでしょうか。
100だったものを95にする(100で割って95を掛ける)
100だったものを108にする(100で割って108を掛ける)
という計算です。
今年の人数を「x , y」として昨年の人数を表わす場合は、この計算を反転させればいいですね。つまり、
95にしたものを100に戻す(95で割って100を掛ける)
108にしたものを100に戻す(108で割って100を掛ける)
という計算をしてあげると、5%減る前の人数、8%増える前の人数、をそれぞれ求めることが出来ます。

これで式が二つ完成したので、あとは連立方程式の計算で解けばいいですね。
今回は求める数である「今年の男子と女子の生徒数」を「x , y」とおいて式を立てているので、計算して求めた「x , y」の値がそのまま答えとなります。
今回の考え方はいかがでしたか?
昨年の生徒数を「x , y」とおくか、今年の生徒数を「x , y」とおくか、たったそれだけの違いですが、式を書くための考え方の難易度はかなり差があるかもしれませんね。
とはいえ、今年の生徒数を「x , y」とおいて式を考えたからこそ、「方程式の文章問題の解き方」ということだけでなく「○%増えたり減ったりした物の数を、○%増えたり減ったりする前の数に戻す、割合の計算の考え方」まで学ぶことが出来るのです。
スタンダードな問題の解き方だけを教える、というのは最短ルートで効率よく思えるかもしれませんが、今回のような考え方を学んで行くことは、たとえ時間がかかって非効率的に思えても、子どもたちの地頭力を育てるとても大切な過程だと考えています。
たくさん寄り道をして、たくさん考えた子ほど、応用力が身に付きます!
ですので当塾ではひとつの考え方だけに囚われず、自由な発想でさまざまな考え方を身につけられるよう、分からない事に対し試行錯誤を重ねていく!そういう学習を大切にしています(^^)
2019年
7月
11日
木
文章問題の考え方講座 ~part1 #1~
文章問題の考え方講座 ~part1~、ということで第1回はこちらの問題について考えてみます。
--------------------------------------------------
ある中学校の昨年の生徒数は、男女あわせて530人であった。今年は、昨年と比べると、男子は5%減り、女子は8%増え、合計では6人増えている。今年の男子と女子の生徒数を、それぞれ求めよ。
--------------------------------------------------
割合の考え方を含む文章問題です。苦手な子も多いですね。
ウチの生徒がこの問題を解くときに、ココが分からなかった、こんな間違いをしていた、っていう実例も元に問題を解くための考え方を見ていきたいと思います。
まずは、この問題を解くのに一番シンプルな考え方から。
文章問題を解くために大切なことは「登場する値とその関係を正しく把握、整理して考えること」かな。この問題であれば、
昨年の男子の生徒数(不明)
昨年の女子の生徒数(不明)
その合計が530人
今年の男子の生徒数(不明、昨年より5%減)
昨年の女子の生徒数(不明、昨年より8%増)
その合計が、昨年より6人増、なので536人
男子の生徒数+女子の生徒数=合計、で等式が書けます。
これらを表にして整理するとこんな感じでしょうか。

次にこの中の「不明な値」に対し、x や y といった記号を置いて、計算によって解を求めるための数式を作っていきます。
このとき、どの値を記号に置き換えて考えるか?、というのはとても大事なポイントで、選択次第でかなり難易度が変わってきます。
この問題では「5%減」「8%増」という値が昨年の人数を元にした変化になっているので、昨年の男女の生徒数を x , y とした方が考えやすいですね。
そこから今年の生徒数を x , y を使ってどのように表すか考えます。
「5%減」は元の人数を100とした場合に、その内の5を減らして95にするということ。
「100→100」は「×1」なので「100→95」は「×0.95」です。
「8%増」は元の人数を100とした場合に、その内の8を増やして108にするということ。
「100→108」は「×1.08」です。
まとめるとこんな感じ。

これで式が二つ書けるのであとは計算するだけですね。
ちなみに求める値が「今年の男子と女子の生徒数」なのに対し、この考え方の式では「昨年の男子と女子の生徒数」を x , y としているので、連立方程式を解いたあと x , y の値から今年の人数をそれぞれ求めないといけない点には注意が必要です。
さて、今回の解説はいかがだったでしょう?
数学の文章問題を解けない子たちは、問題を解く手順が「式を書く」→「計算」の2つだけ。で、式を書く方法は「覚えてる解き方、あるいは似た問題の解き方に数値を当てはめる」ということをしているだけで「問題を読んで式を作る」ということを実はほとんどしていません。
数学が苦手な子たちは「計算することが数学」という感じですが、私の感覚では「計算するまでが数学」です。
なので、これからも式を立てるまでの考え方を色々と解説していきたいと思います(^^)
2019年
7月
07日
日
文章問題の考え方講座 ~part0~
数学の文章問題。苦手な子が多いですね。
多くの子どもが、「解き方」に当てはめて計算し答えを出そう、としかしていないことが多いですね。だから覚えている「解き方」から少しでもズレると、途端に道に迷い、訳が分からなくなってしまうのだと思います。
文章問題を解くのに大切なことは「解き方」ではなく「考え方」です。
では、その「考え方」を養うためにはどうすればいいのでしょうか?
私はあまり小難しくは考えていません。
【寄り道をして、その問題でたくさん遊んでしまえばいい!】
そんな風に考えています。
型にはめて問題を解いて、正解すれば「ハイ終わり」ではなく、
じゃあこうしてみたらどんな式が書けるだろう?
こんな風に考えたら別の式が書けないかな?
と、想像力を膨らませ、一つの問題に ああでもない こうでもない とひたすら思考をめぐらせ自由自在に「解き方」を開発する。
そういう勉強は、未知の問題であろうと解に辿りつける実力が身につくだろうし、なによりきっと楽しい!
そこで当ブログでも「文章問題の考え方講座」シリーズとして、子どもたちが間違いやすいポイントと、それでも躓かずに前に進むための考え方を養っていけるような内容を投稿していけたらと思います。
それでは「文章問題の考え方講座 ~part1~」をお楽しみに(^^)
2015年
8月
04日
火
速さの学習における「距離」と「道のり」の違い
前回 の続き。
さて、「距離」と「道のり」の言葉の違いを勉強したところで、本来のテーマである、
『小・中学生の "速さ" の学習において、「距離」と「道のり」のどちらを用いるべきか』
について考えてみたいと思います。
まず私の考えは、「距離」を使う方が適切、だと感じます。
「速さ」の学習の中では「AとBという二点間の長さ」を考えることもあれば「池の周りだったり、家から学校までといった道の長さ」を考えることもあるわけです。
そのどちらでも使うことのできる「距離」で定義したほうが適切です。
「道のり」とは「道路の距離」に限定した言葉なのだから「AとBという二点間の長さ」というようなことを表わすのには不適切なんですよね。
けれども、どうも学校の教科書では「速さ、時間、道のり」で表記しているようです。
すべての教科書をもっているわけではないので各教科書会社の指導計画作成資料、
東京書籍
http://ten.tokyo-shoseki.co.jp/text/shou/sansu/program.htm
大日本図書
http://www.dainippon-tosho.co.jp/j_school/sansu/archive/guidance_plan.html#no01
学校図書
http://www.gakuto.co.jp/web/jun/junsansu/nenkan/
教育出版
http://www.kyoiku-shuppan.co.jp/view.rbz?cd=2562
啓林館
http://shinko.ee-book.com/h27textbook/math/curriculum/
日本文教出版
http://www.nichibun-g.co.jp/textbooks/sansu/sansu_dl/
を確認してみましたが、ほぼ全ての教科書で「道のり」を使っていました。東京書籍と啓林館のみ「距離」という言葉も使っているようですが、この2社も速さの公式を学ぶところからは全て「道のり」で表記されています。
また、手元に合った教科書「東京書籍:新編 新しい算数6」も確認してみました。
速さの単元はP108~P119で、そのうちP108~P111までは全て「きょり」で表記がされていますが、P112から唐突に「道のり」に変わります。ちょうど公式が登場するところからで、以降は全て「道のり」になっていました。
学校の教科書や準拠ワークなどをみても大体は「道のり」で統一されているようです。
これ、なんで「道のり」になったんでしょうね。「距離」の方が汎用性の高い言葉だと思うのですが。。。
その辺りの経緯なんかも知りたいものです。
さて、ということで結論。
距離と道のりの意味の違いは知っておくべきだが、速さの勉強をする上ではイコールと考えても問題はない
が私の出した答えです。
ここで学ばないといけないことは「速さに関わる数量の関係」を正しく理解すること。
速さと時間から導き出される長さのことを「距離」と「道のり」という記号のどちらで考えたとしても結果は変わらないですし、支障もないです。
なかには表記を統一しないと子どもたちが混乱する、ということをおっしゃる先生もいたりしますが、少なくとも私はその程度のことで混乱するとは思えませんし、そんなことで困っている子どもも見たことはありません。
もし二つの言葉の違いに戸惑う子がいれば、その時は先生が助けてあげればいいだけです。
先生はそういうときのためにいるんですから(^^)
2015年
8月
03日
月
「距離」と「道のり」の意味の違い
すらら導入塾のコミュニティでこんな議論がありました。
『小・中学生の "速さ" の学習において、「距離」と「道のり」のどちらを用いるべきか』
些細なことかもしれませんが、そんな疑問を突き詰めて考える、もっと深く知りたいという知的好奇心に突き動かされた自発的な行動こそが「勉強する」ということだと思っています。
色々と調べてたくさんのことを知ることができたのがとても楽しかったです♪
ということで今回は「距離」と「道のり」の意味の違いについて書きます。
まず、この二つの言葉は小学校3年生の算数ではこのように習います。
・まっすぐにはかった長さを「距離」
・道にそってはかった長さを「道のり」
次に、この二つの言葉の意味を大辞泉で調べてみました。
きょり【距離】
①二つの場所や物事の間の隔たり。
②人との関係で、相手に対する気持ちの上での隔たり。
③数学で、二点を結ぶ線分の長さ。
また、二つの図形上の点を結ぶ線分のうちの最短のものの長さ。
みちのり【道程】
ある地点から他の地点までの道の長さ。目的地までの道路の距離。どうてい。
さて、小3算数習う内容と実際の言葉の意味との間で大きな齟齬は無いように見えますが、決定的な違いが一つあります。
それは小3算数で習う「距離」の定義が「まっすぐな長さ」に限定されてしまっていること。
もちろん「まっすぐな長さ」も「距離」ではあるのだけれど、本来は「まっすぐではない長さ」もまた「距離」なのです。
小3算数で習う内容は、
二つの地点の間を測る方法として「まっすぐに測る方法」と「道に沿って測る方法」とがあるよ。まっすぐに測ったときの長さを「距離」、道に沿って測ったときの長さが「道のり」と区別して覚えよう。
ということです。
「まっすぐ測った長さ」を正しく区別し表現するなら「直線距離」を用いたほうが齟齬は生じないと私は思うのですが、小学3年生の学習ということで長さを測る二つの方法を分かりやすく区別するのに「距離」と「道のり」という言葉を使っているのかもしれません。
「直線距離」を単に「距離」というのも言葉の定義としては正しいですからね。
けれど「距離」と「道のり」の意味を正しく理解させたいなら、やはり「直線距離」という言葉も使って教えてあげたほうがいいような気がします。
ちなみに一応この言葉も大辞泉で調べておきました。
ちょくせんきょり【直線距離】
二点間を結ぶ直線の長さ。平面上の二点間の最短距離。
ということで、まとめると、
二点間の長さを表わす「距離」という大きな概念があり、その中に、「道のり(道路の距離)」や「直線距離(直線の距離)」という言葉がある。
ということだと私は理解しています。
次回は「速さの学習における「距離」と「道のり」の違い」について書こうと思います(^^)
2015年
7月
22日
水
夏休みの宿題より ~○%増えた、減ったの考え方~
塾では生徒の「夏休みの宿題」の面倒(進捗管理と分からない所の指導)も見ているのですが、せっかくなので、生徒から質問があった問題や、多くの生徒がよく分かっていないポイントなんかを、このブログでも取り上げて解説してみたいと思います。
今日は数学の問題からです。
問題:
ある学校の昨年度の生徒数は、男女合わせて650人だったが、
今年度は、男子が3%、女子が4%増えたため、合わせて673人になった。
今年度の男子と女子の生徒数をそれぞれ求めなさい。
連立方程式の問題ですが、式を立てるときに「○%増えた」とか「○%引き」というのを x や y など代数をつかってあらわすのに、どういう式を立てればいいか分からない子が多いみたいです。
さて、この「○%増えた」の考え方ですが、「100人から5%増えた」として考えてみましょう。
100人いたところに100人の5%が増えたのだから、
100 + 100 × 0.05 = 105
これが基本的な考え方ですね。
でも実はもっと簡単な式が書けます。
「人数」ではなく「パーセンテージ」で考えると、元となる人数の100人は「100%」で、そこに「5%」を足すのだから合計で「105%」になるわけですよね。つまり「5%増える」ということは「元の人数の105%になる」ということ。
だからこんな風に計算すればいいわけです。
100 × 1.05 = 105
この考え方さえわかれば x や y などの代数に置き換えても簡単に式が立てられると思います。
ちなみに「○%減る」場合ですが、たとえば10%減ったのなら、100%から10%がなくなるのだから「90%になる」ということ。つまり元の数に0.9をかければいいですね。
ということで「○%増えた、減った」の考え方はしっかり理解しておきましょう(^^)
2015年
2月
22日
日
おうぎ形の面積の求め方
この土日は学年末テスト前ということで教室の方も臨時開校!
生徒たちは全員が4~5時間ほど勉強してくれて、クタクタになりながらも充実感に満ちた表情で帰っていきました(^^)
さて、そのテスト勉強をしている中で、ある生徒がおうぎ形の面積を求める公式について疑問をぶつけてきてくれたので、今日はその疑問を解決してみたいと思います。
おうぎ形の面積は、
「母線の長さ × 弧の長さ ÷ 2」
という公式で求めることが出来るのですが、その生徒は
「確かこう教わった気がする。あれ?こうじゃなかったっけ?わからん。けどなんとなくこの計算でやってた。」
という感じで、それが正しいかどうかの確証すらないまま使っていたようです(^^;
で、その生徒の疑問というのは、なんで母線の長さと弧の長さを掛けて 2 で割ると面積になるの?、ということでしたので解説してみます。

まず、扇形の 「面積」 や 「弧の長さ」 を求める考え方ですが、「母線 x を半径とする円の面積 or 円周」 から 「おうぎ形の中心角の割合」 を掛けることで求めることができます。
母線 x と中心角 θ が分かっている場合、おうぎ形の弧の長さを求める式は次のようになります。
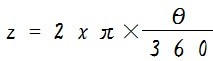
この式を利用して、母線 x と弧の長さ z が分かっていて中心角 θ を求める式を作ると次のようになります。
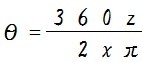
で、扇形の面積は、母線 x と中心角 θ が分かっている場合、式で表すと次のようになります。
(おうぎ形の面積を A とします)
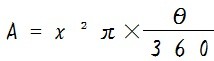
ですが、この式では中心角が分からないと面積は求められないですよね。
けれど、母線 x と弧の長さ z が分かっていれば中心角 θ を求める式が作れましたよね?
なので、これを面積を求める式に代入してみます。
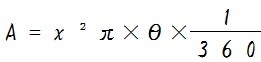

これで中心角が分からなくても母線 x と弧の長さ z さえわかればおうぎ形の面積を求められます。あとはこの式を整理すると、、、
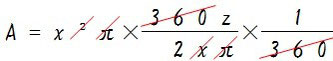
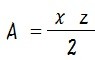
よって、おうぎ形の面積は 「母線の長さ × 弧の長さ ÷ 2」 で求めることができるというわけですね。
2015年
2月
19日
木
円錐の表面積の求め方
今日、生徒が苦戦していた円錐の表面積の求め方について簡単に書いてみたいと思います。

x と y の長さが分かっていて表面積を求めなさい、っていう問題ですね。
立体図形の表面積を求める問題は、立体を平面に、平面を立体に、その図形のイメージを正しく捉えられるか、っていうのが一つのポイントだと思います。
円錐の場合、展開すると、

こんな感じで、おうぎ形と円がくっついた形になります。
それぞれの面積を求めて足せばいいですね。
円の方は 「半径×半径×π」 なので 「y²π」 となります。
おうぎ形の方は、「おうぎ形の弧の長さ」 ÷ 「母線 x を半径とする円の円周」 で円に対するおうぎ形の割合を計算し、円全体の面積からその割合分の面積を求めます。
ちなみに 「おうぎ形の弧の長さ」 は 「半径 y の円の円周」 と同じ長さなのでそこから計算します。
あとはこの二つを足せば円錐の表面積を求めることが出来る、というのが考え方ですね。
さて、ではここで一歩進んで 「もっと楽に求める方法」 について考えてみましょう(^^)
まずは上記の考え方を x と y を使って一つの式として書き出します。(円錐の表面積を A としてます)
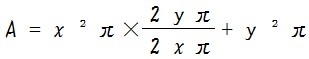
この式を整理すると、
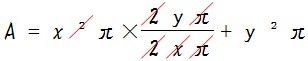
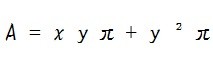
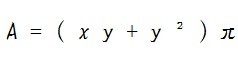
実はこんなに簡単に円錐の表面積を求めることが出来るんですね。
中学一年生の一学期に習った代数の計算を利用すれば複雑な計算も楽に解けてしまうわけです(^^)
とはいえ、この公式を生徒に教えることはしません。
テストの成績を伸ばすことだけが目的ならそれでいいかもせれませんが、本当に伸ばさないといけないのは学ぶ力、考える力です。
子どもたちには、何も考えずただ公式に当てはめて計算をするだけではなく、元となる考え方をきちんと理解してほしいと思っています。
2014年
8月
22日
金
計算の順序
生徒からこんな質問がありました。
一次方程式で数字の項をまとめたときの計算で、
13 - 8 + 5
「これってたし算を先にやってもいいの?ひき算を先にするのと答え変わるんやけど?」
答えは No ですね。
左から順番に計算する、が正解です。
理由は 「それが四則演算の計算のルールだから」 です。
【 13 - 8 + 5 】の計算の意味は、
「13 から 8 を引いて 5 を足す」
ということです。
たし算を先にしてしまうと、
「13 から 8 と 5 を足したものを引く」
という意味なので、
【 13 - ( 8 + 5 ) 】という計算に変わります。
全部たし算にすればわかりやすいのかな。
13 + ( -8 ) + 5
後ろの計算を先にやるというのは 8 + 5 ではなく -8 + 5 という計算をする、ということなんですね。
生徒たちが勉強している中でこのような疑問を持ってくれることは嬉しいことです♪
2014年
7月
11日
金
なんで移項すると符号がかわるの?
今日は方程式を解くときに使う「移項」について書きますね。
「移項」とは、「等式において、一方の辺の項を他方の辺に符号を変えて移すことができる」というルールですね。
例えば、
x+3=10
x=10-3
x=-2x+9
x+2x=9
というように数字や文字の項を符号を変えてもう一方の辺に移すことができます。
では、なぜ移項すると符号が変わるのか?
それは「等式の性質」を利用した結果だから、です。
まずは「等式の性質」について。
・A=B ならば A+C=B+C(両辺に同じ数を足しても等式が成り立つ)
・A=B ならば A-C=B-C(両辺から同じ数を引いても等式が成り立つ)
・A=B ならば AC=BC(両辺に同じ数を掛けても等式が成り立つ)
・A=B ならば A/C=B/C(両辺を同じ数で割っても等式が成り立つ、ただし C≠0)
この性質を利用すると、
① x+3=10
② x+3-3=10-3
③ x=10-3
となります。
②の左辺にある「+3-3」は「0」になるので、これを省力すると③となり、①から③を見ると左辺の「+3」を符号を変えて右辺に移した形になりますよね。
ならば、両辺から「3」を引くというステップは飛ばして、最初から左辺の「+3」を「-3」へと符号を変えて右辺に移してしまおう、というのが移項の考え方となります。
2013年
12月
05日
木
算数と数学の違いって?
先日、ある生徒から「算数と数学ってどう違うの?」と質問を受けました。
うーん。算数と数学の違い。
あまり深く考えたことなかったですね。
例えば子どもたちって「学校の勉強なんて大人になったら使わない」、という
ようなことをよく言うけど、算数なんかは日常生活するうえで必須の学問です
よね。
数学はというと確かに方程式や関数などほとんどは日常生活では使いませんが、
仕事や人生を生きるうえでは数学的なものの考え方は非常に大切なことのよう
に感じます。
とりあえず、その場で上手く言葉に出来なかったので「ちょっと考えさせて」
と言って宿題にさせてもらいました。
で、いろいろ調べたり考えたりして、自分なりに算数と数学の違いを簡潔に
表現すると、
・算数
→日常生活に必要な能力を磨くための学問
・数学
→物事を論理的に考え未知の問題を解決する能力を磨く学問
ということかな、と思います。
質問してくれた子に伝えると、分かったような分からないような、という感じ
でしたけど(^^;;
ともあれ、生徒が「算数と数学の違いは?」って質問してくれたおかげで私も
いろいろ勉強できましたし、新しい発見もたくさんあって、本当に感謝です!!
ちなみに、文部科学省の真学習指導要領では算数・数学で学ぶべき目標を次のように
定義してます。参考までに。
小学校学習指導要領 算数
http://www.mext.go.jp/a_menu/shotou/new-cs/youryou/syo/san.htm
中学校学習指導要領 数学
http://www.mext.go.jp/a_menu/shotou/new-cs/youryou/chu/su.htm